Basis of disinfection - Aquaculture Engineering

Basis of disinfection

Degree of removal

The term percentage removal of actual micro-organisms is used in environmental engineering. In microbiological terms log10 removal or inactivation (decimal removal) is used to define the disinfection yield; normally a reduction of between 99 and 99.99% of the total number of bacteria is wanted, which corresponds to a log disinfection of 2–4. However, these terms do not give exact values of the number of micro-organisms left; they only indicate by how much numbers are reduced from the starting concentration.

Example

The normal concentration of bacteria is 107/ml and a reduction of 99.9% is required. Find the concen-tration of bacteria present after disinfection.

Solution

concentration of bacteria after infection = 107(1 âˆ’ 0.999)

Example

The starting concentration of bacteria is 107/ml. A log disinfection of 3 is wanted. Calculate the new concentration of bacteria.

Solution

Let the starting concentration be N1 and the end con-centration N2; log(disinfection) = 3.

log(disinfection) = log(N1/N2)

= logN1 âˆ’ logN2log N2= log N1−log(disinfection)

=7 â€“ 3

=4

N2=104/ml

Chick’s law

Inactivation of micro-organisms in a disinfection plant depends on the time that the micro-organism are exposed to the disinfectant. This is described by Chick’s law:

dn / dt = kN

where:

dn/dt= necessary time to inactivate n micro-organisms

k =time constant depending on disinfectant,type of micro-organism and water quality

N =number of live micro-organisms t =time.

This differential equation can be integrated within limits to give the following equation:

N1= N0e−kt

where:

N0=number of micro-organisms at the start

N1=number of micro-organisms after time t.

Watson’s law

Based on the results of Chick’s law, Watson’s law can be developed:

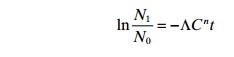
where:

Λ = coefficient of specific toxicity

C =concentration of disinfectant

n =exponent (normally around 1)

t =time after start-up.

This means that the relation between the number of active and inactive micro-organisms is a product of the concentration of the disinfectant and the exposure time.

Dose-response curve

Based on Watsons’s law a dose-response relation may be established for specific types of micro-organism. This gives the proportion of micro-organisms inactivated by fixed doses of disinfectant over various time periods. Exact dose-response relationships are difficult to determine in practice for several reasons. It is often difficult to isolate new pathogens and the response to a certain dose depends, amongst other factors, on the immune status of the organism, environmental conditions and population density.