Arithmetic Mean

Arithmetic Mean

1. Arithmetic Mean-Raw Data

The Arithmetic Mean of a data is the most commonly used of all averages and is found by adding together all the values and dividing by the number of items.

For example, a cricketer, played eight (T20) matches and scored the following scores 25, 32, 36, 38, 45, 41, 35, 36.

Then, the mean of his scores (that is the arithmetic average of the scores) is obtained by

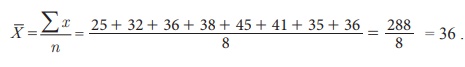
In general, if we have n number of observations x₁, x₂, x₃, …, x_n then their arithmetic mean denoted by  (read as X bar) is given by

We express this as a formula: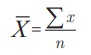 

Assumed Mean method: Sometimes we can make calculations easy by working from an entry that we guess to be the right answer. This guessed number is called the assumed mean.

Note

It does not matter which number is chosen as the assumed mean; we need a number that would make our calculations simpler. Perhaps a choice of number that is closer to most of the entries would help; it need not even be in the list given.

In the example above on cricket scores, let us assume that 38 is the assumed mean. We now list the differences between the assumed mean and each score entered:

25–38 = –13, 32–38 = –6, 36–38 = –2, 38–38 = 0,

45–38 = 7, 41–38 = 3, 35–38 = –3, 36–38 = –2

The average of these differences is [–13–6–2 + 0 +7+3–3–2] / 8 = –16/8 = 2

We add this ‘mean difference’ to the assumed mean to get the correct mean.

Thus the correct mean = Assumed Mean +Mean difference = 38 – 2 = 36 .

This method will be very helpful when large numbers are involved.

2. Arithmetic Mean-Ungrouped Frequency Distribution

Consider the following list of heights (in cm) of 12 students who are going to take part in an event in the school sports.

140, 142, 150, 150, 140, 148, 140, 147, 145, 140, 147, 145.

How will you find the Mean height?

There are several options.

(i) You can add all the items and divide by the number of items.

(14 0 + 142+15 0 + 150 + 14 0 + 148+14 0 + 147+145+14 0 + 147+145) /12

 = 1734/12

=144. 5

(ii) You can use Assumed mean method. Assume, 141 as the assumed mean.

Then the mean will be given by

= [141] + [ (−1) +(1) +(9) +(9) +(−1) +(7) +(−1) +(6) +(4) +(−1) +(6) +(4)]/12

= [141] + [−4+46]/12

=141+ 42/12

= 141+3.5

=144.5

(iii) A third method is to deal with an ungrouped frequency distribution. You find that 140 has occurred 4 times, (implying 4 is the frequency of 140), 142 has occurred only once (indicating that 1 is the frequency of 142) and so on. This enables us to get the following frequency distribution.

You find that there are four 140s; their total will be 140 × 4 = 560

There is only one 142; so the total in this case is  142×1=142

There are two 150s; their total will be 150×2=300 etc.

These details can be neatly tabulated as follows:

Looking at the procedure in general terms, you can obtain a formula for ready use. If x₁, x₂, x₃, … x_n are n observations whose corresponding  frequencies are f₁ , f₂ , f₃ , … f_n then the mean is given by

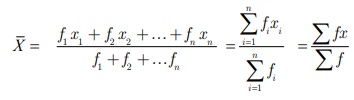
Can you adopt the above method combining with the assumed mean method? Here is an attempt in that direction:

Note: Study each step and understand  the meaning of  each symbol.

 (iv) Let the assumed mean be 145. Then we can prepare the following table:

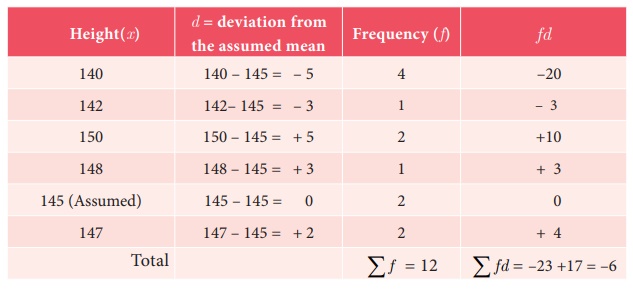
Arithmetic mean = Assumed mean + Average of the sum of deviations

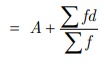
 = A + ∑fd/∑f  = 145+ (–6/12) = 145.0 – 0.5 = 144.5

When large numbers are involved, this method could be useful.

3. Arithmetic Mean-Grouped Frequency Distribution

When data are grouped in class intervals and presented in the form of a frequency table, we get a frequency distribution like this one:

The above table shows the number of customers in the various age groups. For example, there are 120 customers in the age group 20 – 30, but does not say anything about the age of any individual. (When we form a grouped frequency table the identity of the individual observations is lost). Hence we need a value that represents the particular class interval. Such a value is called mid value (mid-point or class mark) The mid-point or class mark can be found using the formula given below.

Mid Value = [UCL + LCL] /2, UCL – Upper Class Limit, LCL – Lower Class Limit 

In grouped frequency distribution, arithmetic mean may be computed by applying any one of the following methods.

(i) Direct Method (ii) Assumed Mean Method (iii) Step Deviation Method

(i) Direct Method

When direct method is used, the formula for finding the arithmetic mean is

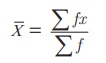
Where x is the mid-point of the class interval and f is the corresponding frequency

Steps

(i) Obtain the mid-point of each class and denote it by x

(ii) Multiply those mid-points by the respective frequency of each class and obtain the sum of fx

(ii) Divide ∑fx by ∑f to obtain mean

Example 8.1

The following data gives the number of residents in an area based on their age. Find the average age of the residents.

Solution

Hence the average age = 28.67.

(ii) Assumed Mean Method

We have seen how to find the arithmetic mean of a grouped data quickly using the direct method formula. However, if the observations are large, finding the products of the observations and their corresponding frequencies, and then adding them is not only difficult and time consuming but also has chances of errors. In such cases, we can use the Assumed Mean Method to find the arithmetic mean of grouped data.

Steps

1. Assume any value of the observations as the Mean (A). Preferably, choose the middle value.

2. Calculate the deviation d = x − A for each class

3. Multiply each of the corresponding frequency ‘f ’ with ‘d’ and obtain ∑fd

4. Apply the formula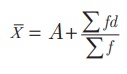 

Example 8.2

Find the mean for the following frequency table:

Solution

Let Assumed mean A = 170

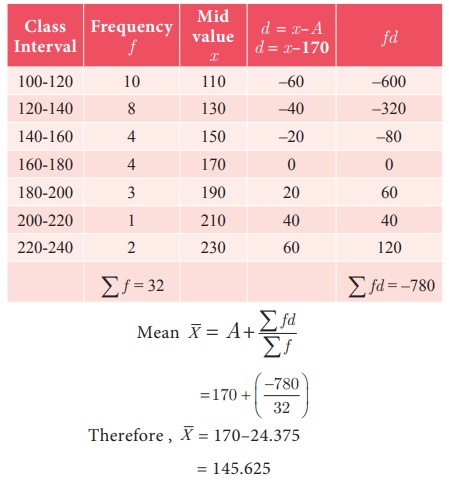
(iii) Step Deviation Method

In order to simplify the calculation, we divide the deviation by the width of class intervals (i.e. calculate (x –A) / c) and then multiply by c in the formula for getting the mean of the data. The formula to calculate the Arithmetic Mean is

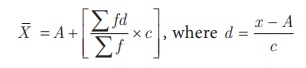
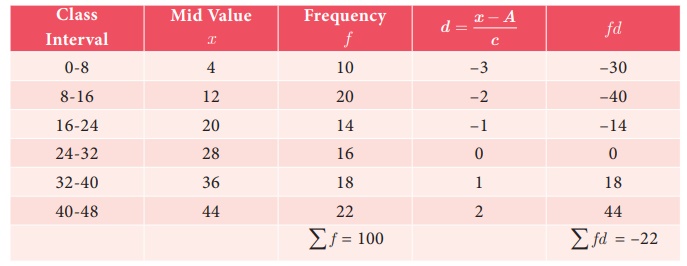
Example 8.3

Find the mean of the following distribution using Step Deviation Method.

Solution

Let Assumed mean A = 28, class width c =8

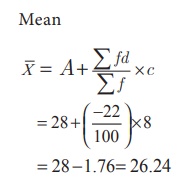
Note

• When x_i and f_i are small, then Direct Method is the appropriate choice.

• When x_i and f_i are numerically large numbers, then Assumed Mean Method or Step Deviation Method can be used.

• When class sizes are unequal and d numerically large,we can still use Step Deviation Method.

4. A special property of the Arithmetic Mean

1. The sum of the deviations of the entries from the arithmetic mean is always zero.

If x₁ , x₂, x ₃ ,..., x_n are n observations taken from the arithmetic mean 

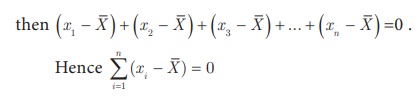
2. If each observation is increased or decreased by k (constant) then the arithmetic mean is also increased or decreased by k respectively.

3. If each observation is multiplied or divided by k, k ≠ 0, then the arithmetic mean is also multiplied or divided by the same quantity k respectively.

Example 8.4

Find the sum of the deviations from the arithmetic mean for the following observations:

21, 30, 22, 16, 24, 28, 18, 17

Solution

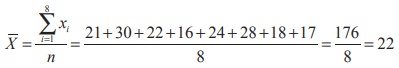
Deviation of an entry x_i from the arithmetic mean  is x_i − , i = 1, 2, ...8.

Sum of the deviations

= (21-22)+(30-22)+(22-22)+(16-22)+(24-22)+(28-22)+(18-22)+(17-22)

= 16–16 = 0. or equivalently, 

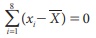
Hence, we conclude that sum of the deviations from the Arithmetic Mean is zero.

Example 8.5

The arithmetic mean of 6 values is 45 and if each value is increased by 4, then find the arithmetic mean of new set of values.

Solution

Let x₁, x₂, x₃, x₄, x₅, x₆ be the given set of values then

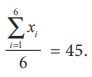
If each value is increased by 4, then the mean of new set of values is

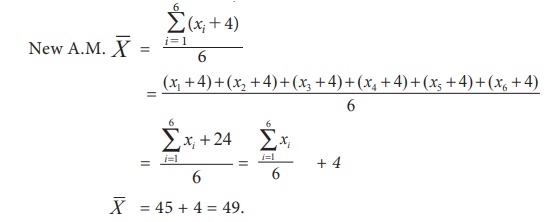
Progress Check

Mean of 10 observations is 48 and 7 is subtracted to each observation, then mean of new observation is __________

Example 8.6

If the arithmetic mean of 7 values is 30 and if each value is divided by 3, then find the arithmetic mean of new set of values

Solution

Let X represent the set of seven values x₁ , x₂ , x₃ , x₄ , x₅ , x₆ , x₇.

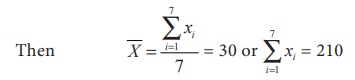
If each value is divided by 3, then the mean of new set of values is

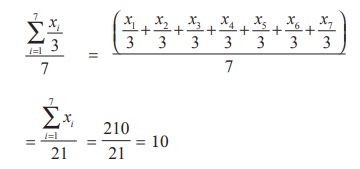
Aliter

If Y is the set of values obtained by dividing each value of X by 3.

Then, 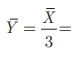 30/3 = 10.

Progress Check

1. The Mean of 12 numbers is 20. If each number is multiplied by 6, then the new mean is __

2. The Mean of 30 numbers is 16. If each number is divided by 4, then the new mean is___

Example 8.7

The average mark of 25 students was found to be 78.4. Later on, it was found that score of 96 was misread as 69. Find the correct mean of the marks.

Solution

Given that the total number of students n = 25,  = 78.4

So, Incorrect ∑x =  × n = 78.4 × 25 = 1960

Correct ∑x = incorrect ∑x − wrong entry + correct entry

= 1960 − 69 + 96 = 1987

Correct  = correct ∑x / n = 1987/25 = 79.48

Progress Check

There are four numbers. If we leave out any one number, the average of the remaining three numbers will be 45, 60, 65 or 70. What is the average of all four numbers?