A Simple Syntax-Directed Translator

Chapter 2

A Simple Syntax-Directed Translator

This chapter is an introduction to the compiling techniques in Chapters 3 through 6 of this book. It illustrates the techniques by developing a working Java program that translates representative programming language statements into three-address code, an intermediate representation. In this chapter, the emphasis is on the front end of a compiler, in particular on lexical analysis, parsing, and intermediate code generation. Chapters 7 and 8 show how to generate machine instructions from three-address code.

We start small by creating a syntax-directed translator that maps infix arithmetic expressions into postfix expressions. We then extend this translator to map code fragments as shown in Fig. 2.1 into three-address code of the form in Fig. 2.2.

The working Java translator appears in Appendix A. The use of Java is convenient, but not essential. In fact, the ideas in this chapter predate the creation of both Java and C.

Figure 2.2: Simplified intermediate code for the program fragment in Fig. 2.1

Introduction

The analysis phase of a compiler breaks up a source program into constituent pieces and produces an internal representation for it, called intermediate code. The synthesis phase translates the intermediate code into the target program.

Analysis is organized around the "syntax" of the language to be compiled. The syntax of a programming language describes the proper form of its pro-grams, while the semantics of the language defines what its programs mean; that is, what each program does when it executes. For specifying syntax, we present a widely used notation, called context-free grammars or BNF (for Backus-Naur Form) in Section 2.2. With the notations currently available, the semantics of a language is much more difficult to describe than the syntax. For specifying semantics, we shall therefore use informal descriptions and suggestive examples.

Besides specifying the syntax of a language, a context-free grammar can be used to help guide the translation of programs. In Section 2.3, we introduce a grammar-oriented compiling technique known as syntax-directed translation. Parsing or syntax analysis is introduced in Section 2.4.

The rest of this chapter is a quick tour through the model of a compiler front end in Fig. 2.3. We begin with the parser. For simplicity, we consider the syntax-directed translation of infix expressions to postfix form, a notation in which operators appear after their operands. For example, the postfix form of the expression 9 - 5 + 2 is 95 - 2+. Translation into postfix form is rich enough to illustrate syntax analysis, yet simple enough that the translator is shown in full in Section 2.5. The simple translator handles expressions like 9 - 5 + 2, consisting of digits separated by plus and minus signs. One reason for starting with such simple expressions is that the syntax analyzer can work directly with the individual characters for operators and operands.

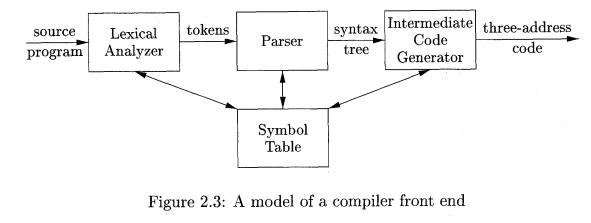
A lexical analyzer allows a translator to handle multicharacter constructs like identifiers, which are written as sequences of characters, but are treated as units called tokens during syntax analysis; for example, in the expression count + 1, the identifier count is treated as a unit. The lexical analyzer in Section 2.6 allows numbers, identifiers, and "white space" (blanks, tabs, and newlines) to appear within expressions.

Next, we consider intermediate-code generation. Two forms of intermedi-ate code are illustrated in Fig. 2.4. One form, called abstract syntax trees or simply syntax trees, represents the hierarchical syntactic structure of the source program. In the model in Fig. 2.3, the parser produces a syntax tree, that is further translated into three-address code. Some compilers combine parsing and intermediate-code generation into one component.

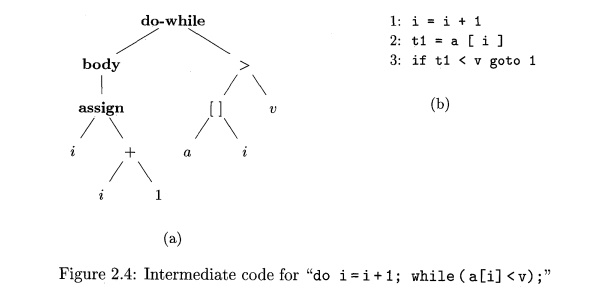
The root of the abstract syntax tree in Fig. 2.4(a) represents an entire do-while loop. The left child of the root represents the body of the loop, which consists of only the assignment i = i + 1 ; . The right child of the root repre-sents the condition a Cil < v. An implementation of syntax trees appears in Section 2.8(a).

The other common intermediate representation, shown in Fig. 2.4(b), is a sequence of "three-address" instructions; a more complete example appears in Fig. 2.2. This form of intermediate code takes its name from instructions of the form x = y op z, where op is a binary operator, y and z the are addresses for the operands, and x is the address for the result of the operation. A three-address instruction carries out at most one operation, typically a computation, a comparison, or a branch.

In Appendix A, we put the techniques in this chapter together to build a compiler front end in Java. The front end translates statements into assembly-level instructions.