A Simple Pointer-Analysis Algorithm

A Simple Pointer-Analysis Algorithm

1 Why is Pointer Analysis Difficult

2 A Model for Pointers and References

3 Flow Insensitivity

4 The Formulation in Datalog

5 Using Type Information

6 Exercises for Section 12.4

In this section, we begin the discussion of a very simple flow-insensitive pointer-alias analysis assuming that there are no procedure calls. We shall show in subsequent sections how to handle procedures first context insensitively, then context sensitively. Flow sensitivity adds a lot of complexity, and is less im-portant to context sensitivity for languages like Java where methods tend to be small.

The fundamental question that we wish to ask in pointer-alias analysis is whether a given pair of pointers may be aliased. One way to answer this question is to compute for each pointer the answer to the question "what objects can this pointer point to?" If two pointers can point to the same object, then the pointers may be aliased.

1. Why is Pointer Analysis Difficult

Pointer-alias analysis for C programs is particularly difficult, because C pro-grams can perform arbitrary computations on pointers. In fact, one can read in an integer and assign it to a pointer, which would render this pointer a potential alias of all other pointer variables in the program. Pointers in Java, known as references, are much simpler. No arithmetic is allowed, and pointers can only point to the beginning of an object.

Pointer-alias analysis must be interprocedural. Without interprocedural analysis, one must assume that any method called can change the contents of all accessible pointer variables, thus rendering any intraprocedural pointer-alias analysis ineffective.

Languages allowing indirect function calls present an additional challenge for pointer-alias analysis. In C, one can call a function indirectly by calling a dereferenced function pointer. We need to know what the function pointer can point to before we can analyze the function called. And clearly, after analyzing the function called, one may discover more functions that the function pointer can point to, and therefore the process needs to be iterated.

While most functions are called directly in C, virtual methods in Java cause many invocations to be indirect. Given an invocation x.m() in a Java program, there may be many classes to which object x might belong and that have a method named m. The more precise our knowledge of the actual type of x, the more precise our call graph is. Ideally, we can determine at compile time the exact class of x and thus know exactly which method m refers to.

Here o is declared to be an Object . Without analyzing what o refers to, all possible methods called "length" declared for all classes must be considered as possible targets. Knowing that o points to a S t r i n g will narrow interprocedural analysis to precisely the method declared for S t r i n g . •

It is possible to apply approximations to reduce the number of targets. For example, statically we can determine what are all the types of objects created, and we can limit the analysis to those. But we can be more accurate if we can discover the call graph on the fly, based on the points-to analysis obtained at the same time. More accurate call graphs lead not only to more precise results but also can reduce greatly the analysis time otherwise needed.

Points-to analysis is complicated. It is not one of those "easy" data flow problems where we only need to simulate the effect of going around a loop of statements once. Rather, as we discover new targets for a pointer, all statements assigning the contents of that pointer to another pointer need to be re-analyzed.

For simplicity, we shall focus mainly on Java. We shall start with flow-insensitive and context-insensitive analysis, assuming for now that no methods are called in the program. Then, we describe how we can discover the call graph on the fly as the points-to results are computed. Finally, we describe one way of handling context sensitivity.

2. A Model for Pointers and References

Let us suppose that our language has the following ways to represent and ma-nipulate references:

1.          Certain program variables are of type "pointer to T" or "reference to T," where T is a type. These variables are either static or live on the run-time stack. We call them simply variables.

2.          There is a heap of objects.  All variables point to heap objects, not to

other variables.  These objects will be referred to as heap  objects.

3. A heap object can have fields, and the value of a field can be a reference to a heap object (but not to a variable).

Java is modeled well by this structure, and we shall use Java syntax in examples. Note that C is modeled less well, since pointer variables can point to other pointer variables in C, and in principle, any C value can be coerced into a pointer.

Since we are performing an insensitive analysis, we only need to assert that a given variable v can point to a given heap object h; we do not have to address the issue of where in the program v can point to h, or in what contexts v can point to h. Note, however, that variables can be named by their full name. In Java, this name can incorporate the module, class, method, and block within a method, as well as the variable name itself. Thus, we can distinguish many variables that have the same identifier.

Heap objects do not have names. Approximation often is used to name the objects, because an unbounded number of objects may be created dynamically. One convention is to refer to objects by the statement at which they are created. As a statement can be executed many times and create a new object each time, an assertion like "v can point to /i" really means "v can point to One or more of the objects created at the statement labeled h." The goal of the analysis is to determine what each variable and each field of each heap object can point to. We refer to this as a points-to analysis; two pointers are aliased if their points-to sets intersect. We describe here an inclusion-based analysis; that is, a statement such as v = w causes variable v to point to all the objects w points to, but not vice versa. While this approach may seem obvious, there are other alternatives to how we define points-to analysis. For example, we can define an equivalence-based analysis such that a statement like v = w would turn variables v and w into one equivalence class, pointing to all the variables that each can point to. While this formulation does not approximate aliases well, it provides a quick, and often good, answer to the question of which variables point to the same kind of objects.

3. Flow Insensitivity

We start by showing a very simple example to illustrate the effect of ignoring control flow in points-to analysis.

Example 1 2 . 2 2 : In Fig. 12.20, three objects, h, i, and j, are created and assigned to variables a, b, and c, respectively. Thus, surely a points to h, b

If you follow the statements (4) through (6), you discover that after line (4) a points only to i. After line (5), b points only to j, and after line (6), c points only to i. •

The above analysis is flow sensitive because we follow the control flow and compute what each variable can point to after each statement. In other words, in addition to considering what points-to information each statement "generates," we also account for what points-to information each statement "kills." For instance, the statement b = c; kills the previous fact "6 points to f and generates the new relationship "6 points to what c points to."

A flow-insensitive analysis ignores the control flow, which essentially assumes that every statement in the program can be executed in any order. It computes only one global points-to map indicating what each variable can possibly point to at any point of the program execution. If a variable can point to two different objects after two different statements in a program, we simply record that it can point to both objects. In other words, in flow-insensitive analysis, an assignment does not "kill" any points-to relations but can only "generate" more points-to relations. To compute the flow-insensitive results, we repeatedly add the points-to effects of each statement on the points-to relationships until no new relations are found. Clearly, lack of flow sensitivity weakens the analysis results greatly, but it tends to reduce the size of the representation of the results and make the algorithm converge faster.

Example 1 2 . 2 3 : Returning to Example 12.22, lines (1) through (3) again tell us a can point to h; b can point to i, and c can point to j. With lines (4) and (5), a can point to both h and i, and b can point to both i and j. With line (6), c can point to h,i, and j. This information affects line (5), which in turn affects line (4), In the end, we are left with the useless conclusion that anything can point to anything.

4. The Formulation in Datalog

Let us now formalize a flow-insensitive pointer-alias analysis based on the dis-cussion above. We shall ignore procedure calls for now and concentrate on the four kinds of statements that can affect pointers:

1. Object creation, h: T v = new T ( ) ; This statement creates a new heap object, and variable v can point to it.

2. Copy statement, v = w; Here, v and w are variables. The statement makes v point to whatever heap object w currently points to; i.e., w is copied into v.

3. Field store, v . f = w; The type of object that v points to must have a field /, and this field must be of some reference type. Let v point to heap object h, and let w point to g. This statement makes the field /, in h now point to g. Note that the variable v is unchanged.

4. Field load, v = w . f ; Here, if is a variable pointing to some heap object that has a field /, and / points to some heap object h. The statement makes variable v point to h.

Note that compound field accesses in the source code such as v = w. f. g will be broken down into two primitive field-load statements:

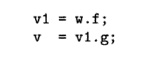
Let us now express the analysis formally in Datalog rules. First, there are only two IDB predicates we need to compute:

1. pts(V,H)  means that  variable  V  can point  to heap object  H.

2. hpts(H, F, G) means that field F of heap object H can point to heap object G.

The EDB relations are constructed from the program itself. Since the location of statements in a program is irrelevant when the analysis is flow-insensitive, we only have to assert in the EDB the existence of statements that have certain forms. In what follows, we shall make a convenient simplification. Instead of defining EDB relations to hold the information garnered from the program, we shall use a quoted statement form to suggest the EDB relation or relations that represent the existence of such a statement. For example, "H : TV = new T" is an EDB fact asserting that at statement H there is an assignment that makes variable V point to a new object of type T. We as-sume that in practice, there would be a corresponding EDB relation that would be populated with ground atoms, one for each statement of this form in the program.

With this convention, all we need to write the Datalog program is one rule for each of the four types of statements. The program is shown in Fig, 12.21. Rule (1) says that variable V can point to heap object H if statement H is an assignment of a new object to V. Rule (2) says that if there is a copy statement V = W, and W can point to H, then V can point to H.

Rule (3) says that if there is a statement of the form V.F = W,W can point to G, and V can point to H, then the F field of H can point to G. Finally, rule (4) says that if there is a statement of the form V = W.F, W can point to G, and the F field of G can point to H, then V can point to H. Notice that pts and hpts are mutually recursive, but this Datalog program can be evaluated by either of the iterative algorithms discussed in Section 12.3.4.

5. Using Type Information

Because Java is type safe, variables can only point to types that are compat-ible to the declared types. For example, assigning an object belonging to a superclass of the declared type of a variable would raise a run-time exception. Consider the simple example in Fig. 12.22, where 5 is a subclass of T. This program will generate a run-time exception if p is true, because a cannot be assigned an object of class T. Thus, statically we can conclude that because of the type restriction, a can only point to h and not g.

Thus, we introduce to our analysis three EDB predicates that reflect impor-tant type information in the code being analyzed. We shall use the following:

1. vType(V,T) says that variable V is declared to have type T.

2. hType(H,T) says that heap object H is allocated with type T. The type of a created object may not be known precisely if, for example, the object is returned by a native method. Such types are modeled conservatively as all possible types.

3. assignable(T, S) means that an object of type S can be assigned to a variable with the type T. This information is generally gathered from the declaration of subtypes in the program, but also incorporates information about the predefined classes of the language. assignable(T:T) is always true.

We can modify the rules from Fig. 12.21 to allow inferences only if the variable assigned gets a heap object of an assignable type. The rules are shown in Fig. 12.23.

The first modification is to rule (2). The last three subgoals say that we can only conclude that V can point to H if there are types T and S that variable V and heap object H may respectively have, such that objects of type S can be assigned to variables that are references to type T. A similar additional restriction has been added to rule (4). Notice that there is no additional restriction in rule (3) because all stores must go through variables. Any type restriction would only catch one extra case, when the base object is a null constant.

6. Exercises for Section 12.4

Exercise 1 2 . 4 . 3 : We can extend the analysis of this section to be interproce-dural if we simulate call and return as if they were copy operations, as in rule (2) of Fig. 12.21. That is, a call copies the actuals to their corresponding formals, and the return copies the variable that holds the return value to the variable that is assigned the result of the call. Consider the program of Fig. 12.25.

a)           Perform an insensitive analysis on this code.

b)          Some of the inferences made in (a) are actually "bogus," in the sense that they do not represent any event that can occur at run-time. The problem can be traced to the multiple assignments to variable b. Rewrite the code of Fig. 12.25 so that no variable is assigned more than once. Rerun the analysis and show that each inferred pts and hpts fact can occur at run time.