2,3 Noded Linear Triangular Element

THREE NODED LINEAR TRIANGULAR ELEMENT

The physical domain considered is geometrically a 2-Dimensional domain, i.e., an area with uniform thickness and the single variable can be one of pressure, temperature, etc. (a scalar quantity, not a vector quantity). An example is the temperature distribution in a plate. At each point there can be only one temperature. We consider such an area meshed with triangular elements. Each triangular element has three nodes, (i.e., one node at each corner). Let us consider one such element with coordinates one such element with coordinates     (x1,y1), (x2,y2), (x3,y3) . The single variable (for example, temperature) at these nodes 1, 2 and 3 are u1 , u 2 and u3 , respectively. If so, then the unknown single variable u (temperature) at any non-nodal point x, y in the 2-D domain can be expressed in terms of the known nodal variables (temperatures) u1 , u 2  and u3.

Let us assume that the single variable can be expressed as

U= c1+c2x+c3y

In order to find the three unknowns c1 , c2  and c3 , we apply the boundary conditions

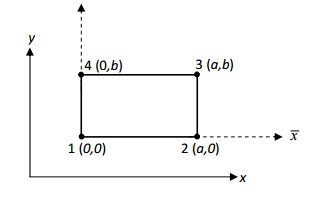
FOUR NODED LINEAR RECTANGULAR ELEMENT

Let us assume that the single variable can be expressed as

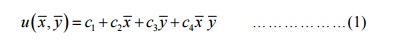
This polynomial contains four linearly independent terms and is linear in x and y, with a bilinear term in x and y. The polynomial requires an element with four nodes. There are two possible geometric shapes: a triangle with the fourth node at the centroid of the triangle or a rectangle with nodes at the vertices.

A triangle with a fourth node at the center does not provide a single-valued variation of u at inter-element boundaries, resulting in incompatible variation of u at inter-element boundaries and is therefore not admissible.

The linear rectangular element is a compatible element because on any side, the single variable u varies only linearly and there are two nodes to uniquely define it.

Here we consider an approximation of the form given in eqauation (1) and use a rectangular element with sides a and b. For the sake of convenience we choose a local coordinate system

(x, y  to derive the interpolation functions.

In order to find the three unknowns c1 , c2  and c3 , we apply the boundary conditions

TWO-VARIABLE 3-NODED LINEAR TRIANGULAR ELEMENT

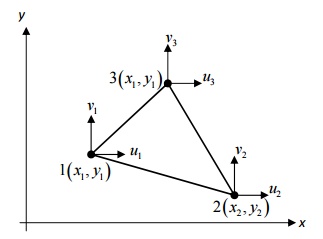
Figure shows a 2-D two-variable linear triangular element with three nodes and the two dof at each node. The nodes are placed at the corners of the triangle. The two variables (dof) are displacement in x-direction (u) and displacement in y-direction (v). Since each node has two dof, a single element has 6 dof. The nodal displacement vector is given by

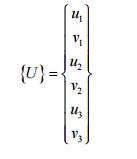
We select a linear displacement function for each dof as

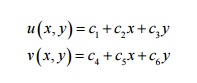
The above two algebraic equations can also be written as

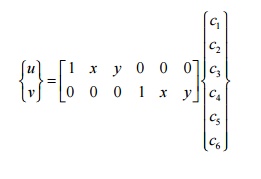
Using steps we had developed for the 2-D single-variable linear triangular element, we can write

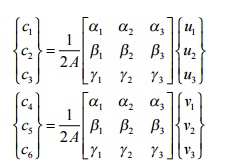
and using the interpolation functions we had developed for the 2-D single-variable linear triangular element, we can write

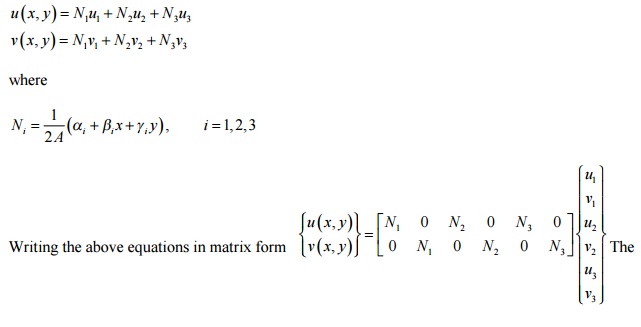
{U }=[N ]{a}

strains associated with the two-dimensional element are given by