Chapter: Mechanical : Strength of Materials : Thin Cylinders, Spheres and Thick Cylinders
Triaxial Stress, Biaxial Stress, and Uniaxial Stress
Triaxial Stress, Biaxial Stress, and Uniaxial Stress
Triaxial stress refers to a condition where only normal stresses act on an element and all shear stresses (txy, txz, and tyz) are zero. An example of a triaxial stress state is hydrostatic pressure acting on a small element submerged in a liquid.
A two-dimensional state of stress in which only two normal stresses are present is called biaxial stress. Likewise, a one-dimensional state of stress in which normal stresses act along one direction only is called a uniaxial stress state.
Pure Shear
Pure shear refers to a stress state in which an element is subjected to plane shearing stresses only, as shown in Figure 3. Pure shear occurs in elements of a circular shaft under a torsion load.
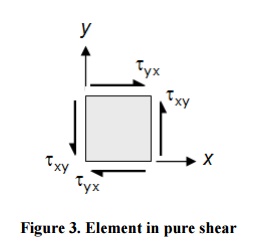
Figure 3. Element in pure shear
Thin cylindrical and spherical shells
Thin-walled assumption
For the thin-walled assumption to be valid the vessel must have a wall thickness of no more than about one-tenth (often cited as one twentieth) of its radius. This allows for treating the wall as a surface, and subsequently using the Young–Laplace equation for estimating the hoop stress created by an internal pressure on a thin wall cylindrical pressure vessel:
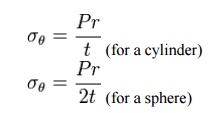
where
· P is the internal pressure
· t is the wall thickness
· r is the inside radius of the cylinder.
· Ro Deta is the hoop stress.
The hoop stress equation for thin shells is also approximately valid for spherical vessels, including plant cells and bacteria in which the internal turgor pressure may reach several atmospheres.
Inch-pound-second system (IPS) units for P are pounds-force per square inch (psi). Units for t, and d are inches (in). SI units for P are pascals (Pa), while t and d=2r are in meters (m).
When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.
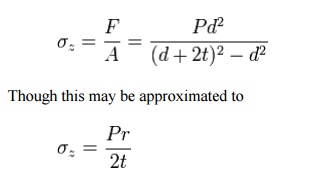
Also in this situation a radial stress is developed and may be estimated in thin walled cylinders as:
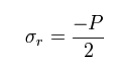
Related Topics