Transshipment Model

THE TRANSSHIPMENT MODEL

The transshipment model recognizes that it may be cheaper to ship through intermediate or transient nodes before reaching the final destination. This concept is more gen-eral than that of the regular transportation model, where direct shipments only are allowed between a source and a destination.

This section shows how a transshipment model can be converted to (and solved as) a regular transportation model using the idea of a buffer.

Example 5.5-1

Two automobile plants, p₁ and p₂, are linked to three dealers, DI, D2, and D3, by way of two transit centers, T1 and T2, according to the network shown in Figure 5.7. The supply amounts at plants PI and P2 are 1000 and 1200 cars, and the demand amounts at dealers Dl, D2, and D3, are 800, 900, and 500 cars. TIle shipping costs per car (in hundreds of dollars) between pairs of nodes are shown on the connecting links (or arcs) of the network.

Transshipment occurs in the network in Figure 5.7 because the entire supply amount of 2200 (= 1000 + 1200) cars at nodes P1 and P2 could conceivably pass through any node of the

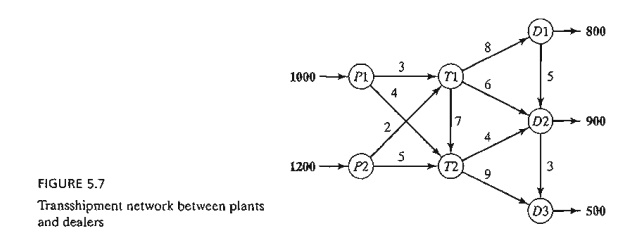
network before ultimately reaching their destinations at nodes D1, D2, and D3. In this regard, each node of the network with both input and output arcs (T1., T2, D1, and D2) acts as both a source and a destination and is referred to as a transshipment node. The remaining nodes are either pure supply nodes (P1 and P2) or pure demand nodes (D3).

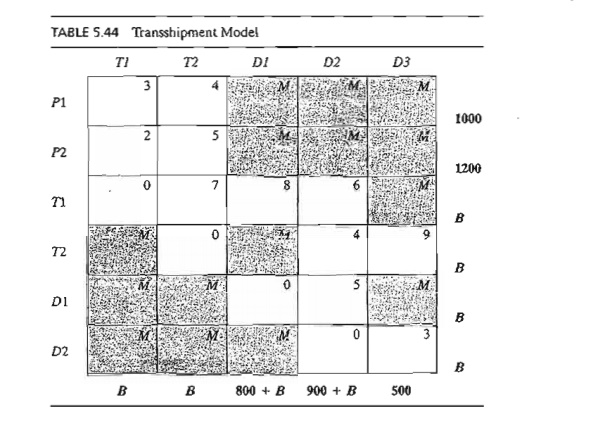
The transshipment model can be converted into a regular transportation model with six sources (P1, P2, T1., T2, Dl, and D2) and five destinations (T1,T2, D1, D2, and D3).1l1e amounts of supply and demand at the different nodes are computed as

Supply at a pure supply node = Original supply

Demand at a pure demand node = Original demand

Supply at a transshipment node = Original supply + Buffer amount

Demand at a transshipment node = Original demand + Buffer amount

The buffer amount should be sufficiently large to allow all of the original supply (or demand) units to pass through any of the transshipment nodes. Let B be the desired buffer amount; then

B = Total supply (or demand)

= 1000 + 1200 (or 800 + 900 + 500)

= 2200 cars

Using the buffer B and the unit shipping costs given in the network; we construct the equivalent regular transportation model as in Table 5.44.

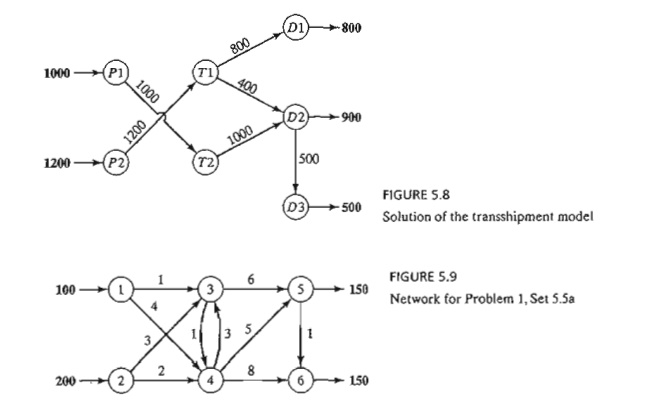
The solution of the resulting transportation model (determined by TORA) is shown in Figure 5.8. Note the effect of transshipment: Dealer D2 receives 1400 cars, keeps 900 cars to sat-isfy its demand, and sends the remaining 500 cars to dealer D3.

PROBLEM SET 5.5A

1. The network in Figure 5.9 gives the shipping routes from nodes 1 and 2 to nodes 5 and 6 by way of nodes 3 and 4. The unit shipping costs are shown on the respective arcs.

a.Develop the corresponding transshipment model.

b.Solve the problem, and show how the shipments are routed from the sources to the destinations.

2. In Problem 1, suppose that source node 1 can be linked to source node 2 with a unit ship-ping cost of $1. The unit shipping cost from node 1 to node 3 is increased to $5. Formulate the problem as a transshipment model, and find the optimum shipping schedule.

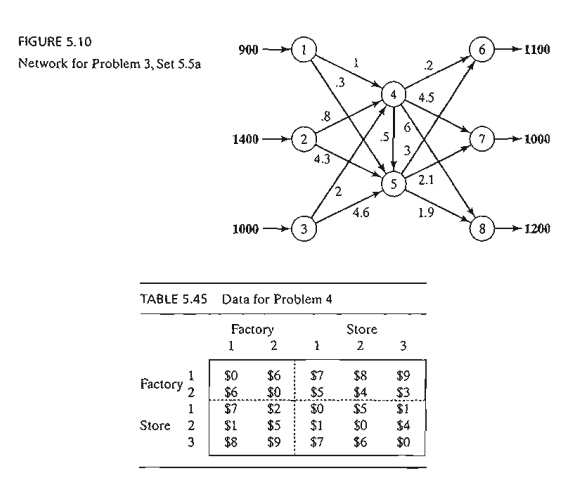
3. The network in Figure 5.10 shows the routes for shipping cars from three plants nodes 1, 2, and 3) to three dealers (nodes 6 to 8) by way of two distribution centers (nodes 4 and 5). The shipping costs per car (in $100) are shown on the arcs.

a. Solve the problem as a transshipment model.

b. Find the new optimum solution assuming that distribution center 4 can sell 240 cars directly to customers.

*4. Consider the transportation problem in which two factories supply three stores with a commodity. The numbers of supply units available at sources 1 and 2 are 200 and 300; those demanded at stores 1,2, and 3 are 100,200, and 50, respectively. Units may be trans-shipped among the factories and the stores before reaching their final destination. Find the optimal shipping schedule based on the unit costs in Table 5.45.

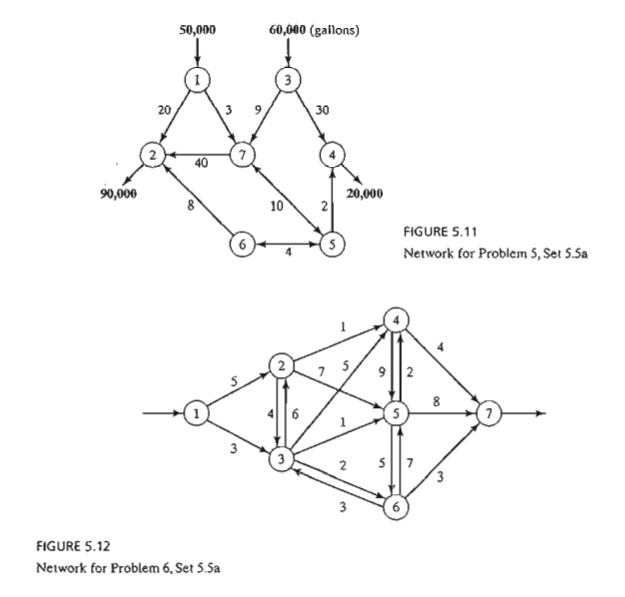
5. Consider the oil pipeline network shown in Figure 5.11. The different nodes represent pumping and receiving stations. Distances in miles between the stations are shown on the network. The transportation cost per gallon between two nodes is directly proportional to the length of the pipeline. Develop the associated transshipment model, and find the op-timum solution.

6. Shortest-Route Problem. Find the shortest route between nodes 1 and 7 of the network in Figure 5.12 by formulating the problem as a transshipment model. The distances between the different nodes are shown on the network. (Hint: Assume that node 1 has a net sup-ply of 1 unit, and node 7 has a net demand also of 1 unit.)

7. In the transshipment model of Example 5.5-1, define Xij as the amount shipped from node i to node j. The problem can be formulated as a linear program in which each node produces a constraint equation. Develop the linear program, and show that the resulting formulation has the characteristic that the constraint coefficients, aij, of the variable x_ij are

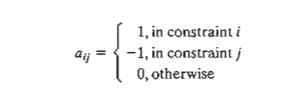
8.    An employment agency must provide the following laborers over the next 5 months:

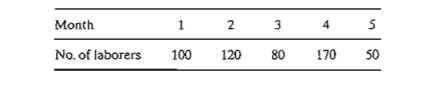
Because the cost of labor depends on the length of employment, it may be more economical to keep more laborers than needed during some months of the 5-month planning horizon. The following table estimates the labor cost as a function of the length of employment:

Formulate the problem as a linear program. Then, using proper algebraic manipulations of the constraint equations, show that the model can be converted to a transshipment model, and find the optimum solution. (Hint: Use the transshipment characteristic in Problem 7 to convert the constraints of the scheduling problem into those of the trans-shipment model.)