Chapter: Mechanical : Design of Transmission Systems : Spur Gears and Parallel Axis Helical Gears
Solved Problems: Spur Gears and Parallel Axis Helical Gears
SOLVED PROBLEMS
1. The following particulars of a single reduction spur gear are given : Gear ratio = 10 : 1; Distance between centres = 660 mm approximately; Pinion transmits 500 kW at 1800 r.p.m.; Involute teeth of standard proportions (addendum = m) with pressure angle of 22.5°; Permissible normal pressure between teeth = 175 N per mm of width. Find :
1. The nearest standard module if no interference is to occur;
2. The number of teeth on each wheel;
3. The necessary width of the pinion; and
4. The load on the bearings of the wheels due to power transmitted.
Solution : Given :
G = TG / TP = DG / DP = 10 ;
L = 660 mm ;
P = 500 kW = 500 × 103 W;
NP = 1800 r.p.m. ; φ = 22.5° ;
WN = 175 N/mm width
1. Nearest standard module if no interference is to occur
Let m = Required module,
TP = Number of teeth on the pinion,
TG = Number of teeth on the gear,
DP = Pitch circle diameter of the pinion, and
DG = Pitch circle diameter of the gear.
We know that minimum number of teeth on the pinion in order to avoid interference,
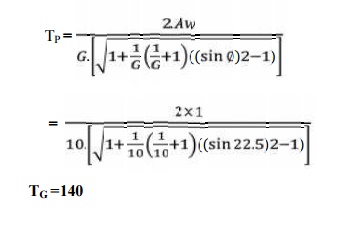
we already know that,
L = (DG / 2) + (Dp / 2) = 5.5 Dp
We also know that
∴ DP = m . TP
= DP / TP = 120 / 14
m = 8.6 mm
Since the nearest standard value of the module is 8 mm, therefore we shall take
m = 8 mm Ans.
2. Number of teeth on each wheel
We know that number of teeth on the pinion,
TP = DP / m = 120 / 8 = 15 Ans.
and number of teeth on the gear,
TG = G × TP = 10 × 15 = 150 Ans.
3. Necessary width of the pinion
We know that the torque acting on the pinion,
T = 60P/(2πN)
= 2652 N-m
Tangential load, WT = T/(DP/2)
= 2652 / (20.12 / 2)
T = 44200 N
WN = Wt/cosϕ
= 44200 / cos 22.5
W = 47 840 N
Since the normal pressure between teeth is 175 N per mm of width, therefore necessary width of
the pinion,
b = 47840 / 175
=273.4 mm Ans.
4. Load on the bearings of the wheels
We know that the radial load on the bearings due to the power transmitted,
WR = WN . sin φ
= 47 840 × sin 22.5°
= 18 308 N
= 18.308 kN An
2. A bronze spur pinion rotating at 600 r.p.m. drives a cast iron spur gear at a transmission ratio of 4 : 1. The allowable static stresses for the bronze pinion and cast iron gear are 84 MPa and 105 MPa respectively. The pinion has 16 standard 20° full depth involute teeth of module 8 mm. The face width of both the gears is 90 mm. Find the power that can be transmitted from the standpoint of strength.
Solution.
Given :
NP = 600 r.p.m. ;
V.R. = TG / TP = 4 ;
σOP = 84 MPa = 84 N / mm2 ; σOG = 105 MPa = 105 N/mm2 ;
TP = 16 ;
m = 8 mm ;
b = 90 mm
We know that pitch circle diameter of the pinion,
DP = m.TP = 8 × 16 = 128 mm = 0.128 m
velocity, ∴ Pitch line
v = πDN/60
= 4.02 m/s
We know that for 20° full depth involute teeth, tooth form factor for the pinion,
yP = 0.154 – (.912/ Tp)
= 0.097
and tooth form factor for the gear
yG = 0.154 – (.912/ TG)
= 0.14
σOP × yP = 84 × 0.097 = 8.148
and σOG × yG = 105 × 0.14 = 14.7
Since (σOP × yP) is less than ( σOG × yG), therefore the pinion is weaker. Now using the Lewis equation for the pinion, we have tangential load on the tooth (or beam strength of the tooth),
WT = σwP.b.π m.yP
= (σOP × Cv) b. π m.yP (Q σWP = σOP.Cv)
= 84 × 0.427 × 90 × π × 8 × 0.097 = 7870 N
∴ Power that can be transmitted = WT × v
= 7870 × 4.02
= 31 640 W
= 31.64 kW Ans.
3. A pair of helical gears are to transmit 15 kW. The teeth are 20° stub in diametral plane and have a helix angle of 45°. The pinion runs at 10 000 r.p.m. and has 80 mm pitch diameter. The gear has 320 mm pitch diameter. If the gears are made of cast steel having allowable static strength of 100 MPa; determine a suitable module and face
width from static strength considerations and check the gears for wear, given σes = 618 MPa.
Solution.
Given :
P = 15 kW = 15 × 103 W;
φ = 20° ; α = 45° ;
NP = 10 000 r.p.m. ;
DP = 80 mm = 0.08 m ;
DG = 320 mm = 0.32 m ;
σOP = σOG = 100 MPa = 100 N/mm2 ; σes = 618 MPa = 618 N/mm2
Module and face width
Let m = Module in mm, and b = Face width in mm.
Since both the pinion and gear are made of the same material (i.e. cast steel), therefore the pinion is weaker. Thus the design will be based upon the pinion.
We know that the torque transmitted by the pinion,
T = (60P) / (2πN)
= 14.32 N-m.
Tangential tooth load on the pinion,
WT = T / (Dp/2)
We know that number of teeth on the pinion,
TP = DP / m = 80 / m
and formative or equivalent number of teeth for the pinion, TE = TP / cos3 α
= 226.4 / m
∴ peripheral velocity,
v = (π Dp Np) / 60
= 42 m/s
Velocity factor, Cv = 0.104
Since the maximum face width (b) for helical gears may be taken as 12.5 m to 20 m, where m is the module, therefore let us take
b = 12.5 m
We know that the tangential tooth load (WT),
358 = (σOP . Cv) b.π m.y'P
= (100 × 0.104) 12.5 m × π m (0.175 – 0.0037 m)
= 409 m2 (0.175 – 0.0037 m)
= 72 m2 – 1.5 m3
Solving this expression by hit and trial method, we find that m = 2.3 say 2.5 mm Ans.
and face width, b = 12.5 m = 12.5 × 2.5 = 31.25 say 32 mm Ans.
Checking the gears for wear
We know that velocity ratio,
V.R. = DG / DP
= 320 / 80
= 4
We know that the maximum or limiting load for wear,
Ww = (D bQK) / cos2a
= 5554 N
A helical cast steel gear with 30° helix angle has to transmit 35 kW at 1500 r.p.m. If the gear has 24 teeth, determine the necessary module, pitch diameter and face width for 20° full depth teeth. The static stress for cast steel may be taken as 56 MPa. The width of face may be taken as 3 times the normal pitch. What would be the end thrust on the gear? The tooth factor for 20° full depth involute gear may be taken as 0.154 – 0.912/T where TE represents the equivalent number of teeth.
Solution.
Given :
α = 30° ;
P = 35 kW = 35 × 103 W ;
N = 1500 r.p.m. ;
TG = 24 ;
φ = 20° ;
σo = 56 MPa = 56 N/mm2 ; b = 3 × Normal pitch = 3 pN
Module
Let m = Module in mm, and
DG = Pitch circle diameter of the gear in mm. We know that torque transmitted by the gear,
T = (60P) / (2πN)
= 223x103 N-mm.
Formative or equivalent number of teeth,
TE = TP / cos3 α
= 37.
∴ Tooth factor, y' = 0.154 – 0.912/T
= 0.129
Tangential tooth load on the pinion,
WT = T / (Dp/2)
∴ = 18600 / m peripheral velocity,
v = (π Dp Np) / 60
= 1.885m m/s
Velocity factor, Cv = 0.75 / (0.75 + v )
= 0.75 / (0.75 + 1.885m )
We know that tangential tooth load,
WT = (σo × Cv) b. π m.y' = (σo × Cv) 3pN × π m × y'
= (σo × Cv) 3 × pc cos α × π m × y'
α)
= (σo × Cv) 3 π m cos α × π m × y'
... (Q b = 3 pN)
... (Q pN = pc cos
... (Q pc = π m)
Solving this equation by hit and trial method, we find that
m = 5.5 say 6 mm Ans
Pitch diameter of the gear
We know that the pitch diameter of the gear,
DG = m × TG = 6 × 24 = 144 mm Ans.
Face width
It is given that the face width,
b = 3 pN = 3 pc cos α = 3 × π m cos α
= 3 × π × 6 cos 30°
= 48.98 say 50 mm Ans.
End thrust on the gear
We know that end thrust or axial load on the gear,
WA = Wr tan a
= 1790 N
Related Topics