Bevel, Worm and Cross Helical Gears

BEVEL, WORM AND CROSS HELICAL GEARS

Common terms used:

1. Pitch cone. It is a cone containing the pitch elements of the teeth.

2. Cone centre. It is the apex of the pitch cone. It may be defined as that point where the axes of two mating gears intersect each other.

3. Pitch angle. It is the angle made by the pitch line with the axis of the shaft. It is denoted by ‘θP’.

Cone distance. It is the length of the pitch cone element. It is also called as a pitch cone radius. It is denoted by ‘OP’. Mathematically, cone distance or pitch cone radius,

5. Addendum angle. It is the angle subtended by the addendum of the tooth at the cone centre. It is denoted by ‘α’ Mathematically, addendum angle,

α = tan–1 (a/OP)

where a = Addendum, and OP = Cone distance.

6. Dedendum angle. It is the angle subtended by the dedendum of the tooth at the cone centre. It is denoted by ‘β’. Mathematically, dedendum angle,

β = tan–1 (d/OP)

where d = Dedendum, and OP = Cone distance.

7. Face angle. It is the angle subtended by the face of the tooth at the cone centre. It is denoted by ‘φ’. The face angle is equal to the pitch angle plus addendum angle.

8. Root angle. It is the angle subtended by the root of the tooth at the cone centre. It is denoted by ‘θR’. It is equal to the pitch angle minus dedendum angle.

9. Back (or normal) cone. It is an imaginary cone, perpendicular to the pitch cone at the end of the tooth.

10.            Back cone distance. It is the length of the back cone. It is denoted by ‘RB’. It is also called back cone radius.

11.            Backing. It is the distance of the pitch point (P) from the back of the boss, parallel to the pitch point of the gear. It is denoted by ‘B’.

Crown height. It is the distance of the crown point (C) from the cone centre (O), parallel to the axis of the gear. It is denoted by ‘HC’.

13.            Mounting height. It is the distance of the back of the boss from the cone centre. It is denoted by ‘HM’.

14.            Pitch diameter. It is the diameter of the largest pitch circle.

15.            Outside or addendum cone diameter. It is the maximum diameter of the teeth of the gear. It is equal to the diameter of the blank from which the gear can be cut. Mathematically, outside diameter,

DO = DP + 2 a cos θP

where DP = Pitch circle diameter,

a = Addendum, and

θP = Pitch angle.

16. Inside or dedendum cone diameter. The inside or the dedendum cone diameter is given by

Dd = DP – 2d cos θP

where          Dd = Inside diameter, and

d = Dedendum.

Design procedure for Bevel Gear

17. Calculation of gear ratio (i) and pitch angle:

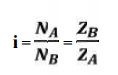
where, N_A and N_B = speed of the driver and driven respectively, and Z_A and Z_B = Number of teeth on driver and driven respectively.

18. Selection of material

Consulting Table 5.3, knowing the gear ratio i, choose the suitable material.

19.                        If not given, assume gear life (say 20000 hrs)

20.                        Calculation of initial design torque:

[M_t] = M_{t .} K. K_d

where,        [M_t] = transmission torque

K   = Load factor, Table 5.11

K_d  = Dynamic load factor, Table 5.12

Assume K. K_d = 1.3 ( if not given)

21.                        Calculation of E_eq, [ϭ_b] and [ϭ_c]:

ü From table 5.20 Calculate E_eq

ü Calculate Design bending stress  [ϭ_b]

[ϭ_b] = (1.4 K_bl/n.Kσ) σ_-1, for one rotation [ϭ_b] = (K_bl/n.Kσ) σ_-1, for both rotation

ü Calculate Design contact stress [ϭ_c] by [ϭ_c] = C_B . HB. K_cl (or)

[ϭ_c] = C_R . HRC. K_cl

where,       C_B C_R = Coefficient of surface hardness from table 5.18

HB HRC = Hardness number

22.Calculation if cone distance (a):

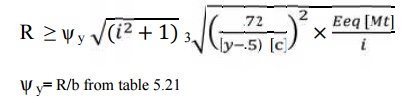
23.     Select number of teeth on gear and pinion:

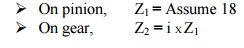
24. Calculation of module:

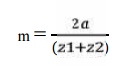
Choose standard module from table 5.8

25. Revision of cone distance (m):

26.     Calculate b, d1av, v and ѱy :

       Calculate face width,      b        =       R/ѱy

       Calculate pitch dia,        d1av  =  mav.z1

       Calculate pitch line velocity,   v        =  (πd1avN1)/60

       Calculate value of ѱp     =       b /d1av

27. Selection of quality of gear:

Knowing the pitch line velocity and acosulting table 5.22, select a suitable quality

of gear.

28. Revision of design torque [M_t]: Revise K:

Using the calculated value of ѱ_y revise the K value by using table 5.11

Revise K_d:

Using the selected quality if gear and pitch line velocity, revise the K_d

value.

[M_t] = M_{t .} K. K_d

29. Check for bending:

Calculate induced bending stress,

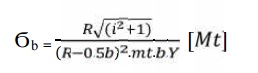
       Compare Ϭb and [Ϭb].

       If Ϭb ≤ [Ϭb], then design is safe.

30. Check for wear strength:

Calculate induced contact stress,

If Ϭc ≤ [Ϭc], then design is safe.

31.     If the design is not satisfactory (ϭb > [ϭb] and / or ϭc > [ϭc] ), then increase the module of face width value of the gear material.

32.     Check for gear:

e.       Check for bending:

Using Ϭb1.y1  and Ϭb1..y1,

Ϭb2 =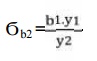 

Compare Ϭb2 and [Ϭb2].

If Ϭb2 ≤ [Ϭb2], then design is safe.

f.       Check for wear strength:

Calculate induced contact stress will be same for pinion and gear,

So,

Ϭc2 = Ϭc

Compare Ϭc and [Ϭc]

If Ϭc ≤ [Ϭc], then design is safe

WORM GEAR

Common terms used :

The following terms, in connection with the worm gearing, are important from the subject point of view :

1. Axial pitch. It is also known as linear pitch of a worm. It is the distance measured axially (i.e. parallel to the axis of worm) from a point on one thread to the corresponding point on the adjacent thread on the worm, as shown in Fig. 31.3. It may be noted that the axial pitch (pa) of a worm is equal to the circular pitch ( pc ) of the mating worm gear, when the shafts are at right angles.

2.  Lead. It is the linear distance through which a point on a thread moves ahead in one revolution of the worm. For single start threads, lead is equal to the axial pitch, but for multiple start threads, lead is equal to the product of axial pitch and number of starts. Mathematically,

Lead, l = pa . n

where          pa = Axial pitch ; and

n = Number of starts.

3. Lead angle. It is the angle between the tangent to the thread helix on the pitch cylinder and the plane normal to the axis of the worm. It is denoted by λ.

A little consideration will show that if one complete turn of a worm thread be imagined to be unwound from the body of the worm, it will form an inclined plane whose base is equal to the pitch circumference of the worm and altitude equal to lead of the worm.

DW  = Pitch circle diameter of worm.

The lead angle (λ) may vary from 9° to 45°. It has been shown by F.A. Halsey that a lead angle less than 9° results in rapid wear and the safe value of λ is 12½°.

4. Tooth pressure angle. It is measured in a plane containing the axis of the worm and is equal to one-half the thread profile angle as shown in Fig. Normal pitch. It is the distance measured along the normal to the threads between two corresponding points on two adjacent threads of the worm.

Mathematically,

Normal pitch, pN = pa.cos λ

Note. The term normal pitch is used for a worm having single start threads. In case of a worm having multiple start threads, the term normal lead (l N) is used, such that

lN = l . cos λ

6. Helix angle. It is the angle between the tangent to the thread helix on the pitch cylinder and the axis of the worm. It is denoted by αW,. The worm helix angle is the complement of

worm lead angle, i.e.

αW + λ = 90°

It may be noted that the helix angle on the worm is generally quite large and that on the worm gear is very small. Thus, it is usual to specify the lead angle (λ) on the worm and helix angle (αG) on the worm gear. These two angles are equal for a 90° shaft angle.

7. Velocity ratio. It is the ratio of the speed of worm (NW) in r.p.m. to the speed of the worm gear (NG) in r.p.m. Mathematically, velocity ratio,

V.R. = N_w / N_G

Let     l = Lead of the worm, and

DG = Pitch circle diameter of the worm gear.

We know that linear velocity of the worm,

vW = l . NW/60

where n = Number of starts of the worm.

DESIGN PROCEDURE FOR WORM GEAR:

1.     Selection of the material:

2.     Calculation of teeth:

ü Assume Z₁ depending upon the number of stat.

ü Z₂ = i X Z₁

3.     Calculation of diameter factor and lead angle

q = d1/m_x

If not given assume q= 11

ɤ    = tan^-1 (z1/q)

4.     Calculation of Tangential load:

F_t = (p/v) x K₀

5.  Calculation of Dynamic load:

F_d = F_t / c_v

6.  Calculation of Beam strength:

F_s = π m_x b [ϭ_b] y

7.  Calculation of Axial load:

Calculate axial load by equating F_{d and} F_s

8.     Calculate b, d2, v.

9.     Recalculation of beam strength

F_s = π m_x b [ϭ_b] y¹

10. Recalculation of dynamic load

F_d = F_t / c_v

11. Check for beam strength:

If F_d ≤ F_d,  design is satisfactory.

12. Calculation for maximum wear load:

F_w = d2. b . K_w

13. Check for wear strength:

If F_d ≤ F_w,  design is satisfactory.

14.                        Calculate power loss and area:

15.                        Calculate basic dimensions.

SOLVED PROBLEMS

1. For continuous duty in a speed reducer, two helical gears are to be rated at 7.4 hp at a pinion speed of 1750 rpm; m_w » 2.75 ; the helix angle 15^o ; 20^o F.D. teeth in the normal plane; let N _p = 21 teeth, and keep b < 2D_p . Determine the pitch, face, N _g , and the material and heat treatment. Use through-hardened teeth with a maximum of 250 BHM (teeth may be cut after heat treatment).

Solution:

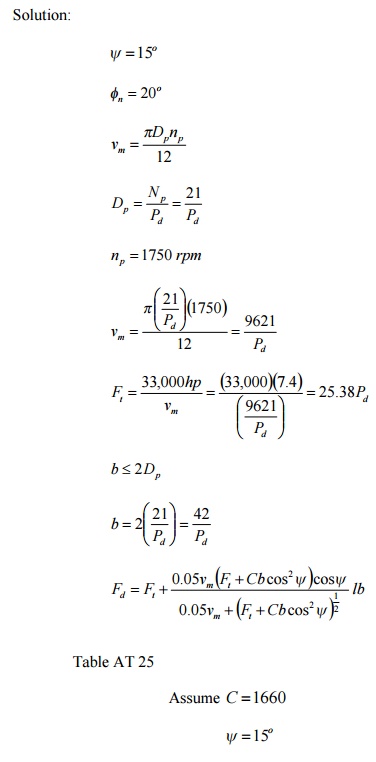
s_u  = 3(29,892) = 89,676 psi

Use C1050, OQT 1100 F,

s_u  = 122 ksi , BHN = 248 < 250

Ans.

P_d  = 6

b = 7 in

N _g  = m_w N _p  = (2.75)(21) = 58

Material. C1050, OQT 1100 F

2.       A pair of helical gears, subjected to heavy shock loading, is to transmit 50 hp at 1750 rpm of the pinion.;  m_g   y = 15 ; minimum  Dp = 4 3/4        in. ; continuous service, 24 hr/day; 20^o F.D. teeth in the normal plane, carefully cut; through-hardened to a maximum BHN = 350. Decide upon the pitch, face width, material and its treatment.

Solution:

Fig. AF 19, v_m  = 2176 fpm

Permissible error = 0.0014 in

Use carefully cut gears, e = 0.001in , P_d  = 5 as standard

Table AT 25,

Steel and steel, 20^o FD

C = 1660

for 24 hr/day service, heavy shock loading

N_sf  = 1.75

0.32955s = (1.75)(5203)

s = 27,629 psi

use sn = su   3

s_u  = 3(27,629) = 82,887 psi

Table AT 9

Use 4150, OQT 1200 F,

s_u  = 159ksi , BHN = 331< 350

Ans.

P_d  = 5

b = 5 in

Material. 4150, OQT 1200 F

Two helical gears are used in a single reduction speed reducer rated at 27.4 hp at a motor speed of 1750 rpm; continuous duty. The rating allows an occasional 100 % momentary overload. The pinion has 33 teeth. P_dn = 10 , b = 2 in. , f_n = 20 , y = 20 , m_w = 2.82 . For both gears, the teeth are carefully cut from SAE 1045 with BHN = 180. Compute (a) the dynamic load, (b) the endurance strength; estimate K _f = 1.7 . Also decide whether or not the 100 % overload is damaging. (c) Are these teeth suitable for continuous service? If they are not suitable suggest a cure. (The gears are already cut.)

Solution: