Definition, Theorem, Illustration, Example, Solution | Mathematics - Sequences | 10th Mathematics : UNIT 2 : Numbers and Sequences
Chapter: 10th Mathematics : UNIT 2 : Numbers and Sequences
Sequences
Sequences
Consider the following
pictures
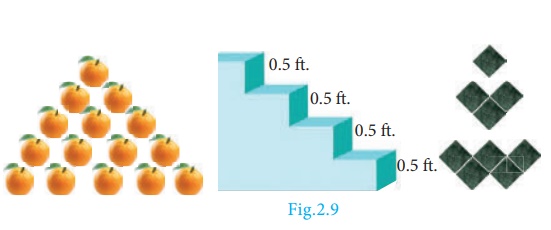
There is some pattern or arrangement in these pictures. In the first picture, the first row contains one apple, the second row contains two apples and in the third row there are three apples etc... The number of apples in each of the rows are 1, 2, 3, ...
In the second picture
each step have 0.5 feet height. The total height of the steps from the base are
0.5 feet,1 feet, 1.5 feet,... In the third picture one square, 3 squares, 5
squares, ....
These numbers belong
to category called “Sequences”.
Definition
A real valued sequence
is a function defined on the set of natural numbers and taking real values
Each element in the sequence is
called a term
of the sequence. The
element in the first position is called the first term of the sequence. The element in the second position is called second term of the sequence and so
on’
If the nth
term is denoted by an, then a1 is the first term, a2 is the second
term, and so on.
A sequence can be
written as a1, a2, a3, …… an,
…
Illustration
1. 1,3,5,7,... is a
sequence with general term an = 2n − 1 . When we put n
= 1, 2, 3,..., we get a1 =1, a2 = 3, a3
= 5, a4 = 7,...
2. 1/2 , 1/3 , 1/4 , 1/5
,... is a sequence with general term 1/ [n
+ 1] . When we put n = 1,2,3,.... we get
a1 = 1/2 , a2 = 1/3 , a3 = 1/4 , a4 = 1/5 ,...
If the number of elements
in a sequence is finite then it is called a Finite sequence. If the number of elements in a
sequence is infinite then it is called an Infinite sequence
Sequence as a Function
A sequence can be
considered as a function defined on the set of natural numbers N. In
particular, a sequence is a function f : N → R , where R
is the set of all real numbers.
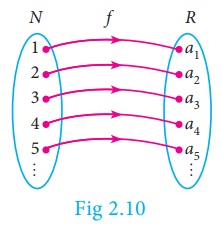
If the sequence is of the form a1,a2,a3,... then we can associate the function to the sequence a1,a2,a3,... by f (k) = ak , k = 1,2,3,...
Example 2.19
Find the next three
terms of the sequences
(i) 1/16 , 1/6 , 1/14 , . . . . (ii) 5, 2,- 1, -4,. . . . (iii) 1, 0.1,
0.01,. . .
Solution
(i) 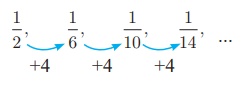
In the above sequence
the numerators are same and the denominator is increased by 4.
So the next three
terms are
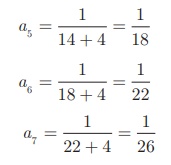
(ii) 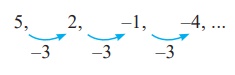
Here each term is
decreased by 3. So the next three terms are -7, -10, -13 .
(iii) 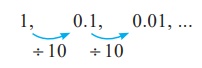
Here each term is
divided by 10. Hence, the next three terms are
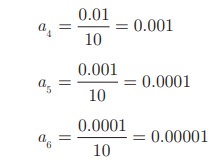
note
Though all the
sequences are functions, not all the functions are sequences.
Example 2.20
Find the general term
for the following sequences
(i) 3, 6, 9,... (ii) 1/2 , 2/3 , 3/4 ,... (iii) 5, -25, 125,...
Solution
(i) 3, 6, 9,...
Here the terms are
multiples of 3. So the general term is
a n = 3n,
(ii) 1/2 , 2/3 , 3/4 ,...
a1 = 1/2 ; a2 = 2/3 ; a3 = 3/4
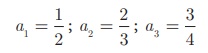
We see that the
numerator of nth term is n, and the denominator is one
more than the numerator.
Hence, an = n / [n+ 1] ,
n ∈ N
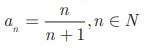
(iii) 5, -25, 125,...
The terms of the
sequence have + and – sign alternatively and also they are in powers of 5.
So the general term a
n = (−1)n +1 5n
,n ∈ N
Example 2.21
The general term of a
sequence is defined as
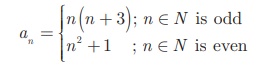
Find the eleventh and
eighteenth terms.
Solution
To find a11 , since 11 is odd, we put n =
11 in an = n(n + 3)
Thus, the eleventh term a11
= 11(11 + 3) = 154 .
To finda18
, since 18 is even, we put n = 18
in a n = n2 + 1
Thus, the eighteenth
term
a18 = 18 2
+ 1 = 325.
Example 2.22
Find the first five
terms of the following sequence.
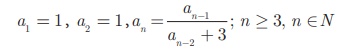
Solution
The first two terms of
this sequence are given bya1 = 1 , a2 = 1. The third term a3 depends on the first and
second terms.
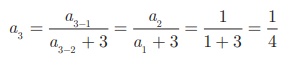
Similarly the fourth
term a4 depends upon a2 and a3
.
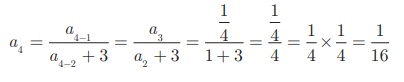
In the same way, the
fifth term a5 can be calculated as
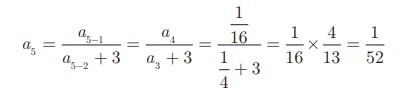
Therefore, the first
five terms of the sequence are 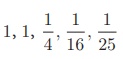
Related Topics