Points to Remember

Points to Remember

Euclid’s division lemma

If a and b are two positive integers then there exist unique integers q and r such that a = bq + r, 0 ≤ r < |b|

Fundamental theorem of arithmetic

Every composite number can be expressed as a product of primes and this factorization is unique except for the order in which the prime factors occur.

Arithmetic Progression

(i) Arithmetic Progression is a ,  a + d ,  a + 2d ,  a + 3d,….n^th term is given by t_n  = a + (n −1)d

(ii) Sum to first n terms of an A.P. is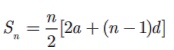 

(iii) If the last term l (n^th  term is given, then S_n  =  )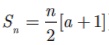

Geometric Progression

(i) Geometric Progression is a ,  ar ,  ar² ,….,ar^n−1 . n^th  term is given by t_n= ar ^n−1

(ii) Sum to first n terms of an G.P. is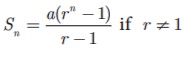 

(iii) Suppose r =1 then S _n  = na

(iv) Sum to infinite terms of a G.P. a + ar + ar² +  is 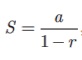  Where –1< r < 1

Special Series

(i) The sum of first n natural numbers 1 + 2 + 3 +  + n =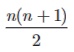 

(ii) The sum of squares of first n natural numbers

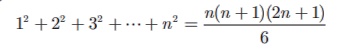
(iii) The sum of cubes of first n natural numbers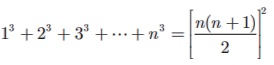 

(iv) The sum of first n odd natural numbers 1 + 3 + 5 + .... ..  + (2n − 1) = n²