Piece Wise Continuous Trial Function

PIECE WISE CONTINUOUS TRIAL FUNCTION

In weighted residual method the polynomial and trigonometric series are u sed as trial function. This trial function is a single composite function and it is valid over the entire solution domain this assumed trial function solution should match closely to the exact solution of the differential equation and the boundary conditions, it i s nothing but a process of curve fitting. This curve fitting is carried out by piecewise method i.e., the more numbers of piece leads better curve fit. P iecewise method can be explained by the following si mple problem.

We know that the straight line can be drawn through any two points. Let, ƒ(x)=sin is the approx imated function for straight line segments.

One straight line segment

Two straight line segment

One Spring Element

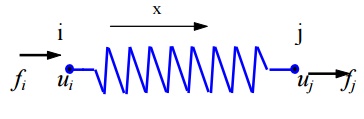
Two nodes: i, j     

Nodal displacements:     ui,      uj (in, m, mm)

Nodal forces:        fi,      fj (lb, Newton) Spring constant (stiffness):   k  (lb/in,

N/m, N/mm)                  

Spring force-displacement relationship:              

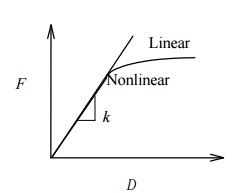
k   F / (> 0) is the force needed to produce a unit stretch.

We only consider linear problems in this introductory course. Consider the equilibrium of forces for the spring.

At node 1 we have

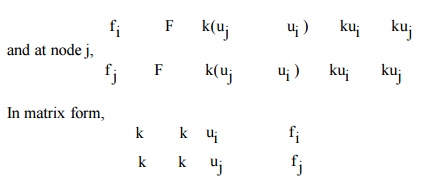
or, where

(element) stiffness matrix

u = (element nodal) displacement vector

f  = (element nodal) force vector

Note:

That k is symmetric. Is k singular or non singular? That is, can we solve the equation? If not, why?

Problem 4

To find the deformation of the shape

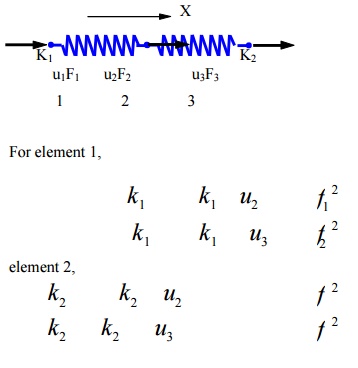
where  fI at  node 2 F2

M is the (internal) force acting on local node i of element Consider the quilibrium of forces at node

Checking the Results

Deformed shape of the structure

Balance of the external forces

Order of magnitudes of the numbers

Notes about the Spring Elements

Suitable for stiffness analysis

Not suitable for stress analysis of the spring itself

Can have spring elements with stiffness in the lateral direction, Spring elements for torsion, etc.