General Definitions of Second and Third Normal Forms

General Definitions of Second and Third Normal Forms

In general, we want to design our relation schemas so that they have neither partial nor transitive dependencies because these types of dependencies cause the update anomalies discussed in Section 15.1.2. The steps for normalization into 3NF relations that we have discussed so far disallow partial and transitive dependencies on the primary key. The normalization procedure described so far is useful for analysis in practical situations for a given database where primary keys have already been defined. These definitions, however, do not take other candidate keys of a relation, if

Table 15.1    Summary of Normal Forms Based on Primary Keys and Corresponding Normalization

any, into account. In this section we give the more general definitions of 2NF and 3NF that take all candidate keys of a relation into account. Notice that this does not affect the definition of 1NF since it is independent of keys and functional dependencies. As a general definition of prime attribute, an attribute that is part of any candidate key will be considered as prime. Partial and full functional dependencies and transitive dependencies will now be considered with respect to all candidate keys of a relation.

1. General Definition of Second Normal Form

Definition. A relation schema R is in second normal form (2NF) if every non-prime attribute A in R is not partially dependent on any key of R.

The test for 2NF involves testing for functional dependencies whose left-hand side attributes are part of the primary key. If the primary key contains a single attribute, the test need not be applied at all. Consider the relation schema LOTS shown in Figure 15.12(a), which describes parcels of land for sale in various counties of a state. Suppose that there are two candidate keys: Property_id# and {County_name, Lot#}; that is, lot numbers are unique only within each county, but Property_id# numbers are unique across counties for the entire state.

Based on the two candidate keys Property_id# and {County_name, Lot#}, the functional dependencies FD1 and FD2 in Figure 15.12(a) hold. We choose Property_id# as the primary key, so it is underlined in Figure 15.12(a), but no special consideration will be given to this key over the other candidate key. Suppose that the following two additional functional dependencies hold in LOTS:

FD3: County_name → Tax_rate

FD4: Area → Price

In words, the dependency FD3 says that the tax rate is fixed for a given county (does not vary lot by lot within the same county), while FD4 says that the price of a lot is determined by its area regardless of which county it is in. (Assume that this is the price of the lot for tax purposes.)

The LOTS relation schema violates the general definition of 2NF because Tax_rate is partially dependent on the candidate key {County_name, Lot#}, due to FD3. To nor-malize LOTS into 2NF, we decompose it into the two relations LOTS1 and LOTS2, shown in Figure 15.12(b). We construct LOTS1 by removing the attribute Tax_rate that violates 2NF from LOTS and placing it with County_name (the left-hand side of FD3 that causes the partial dependency) into another relation LOTS2. Both LOTS1 and LOTS2 are in 2NF. Notice that FD4 does not violate 2NF and is carried over to LOTS1.

2. General Definition of Third Normal Form

Definition. A relation schema R is in third normal form (3NF) if, whenever a nontrivial functional dependency X → A holds in R, either (a) X is a superkey of R, or (b) A is a prime attribute of R.

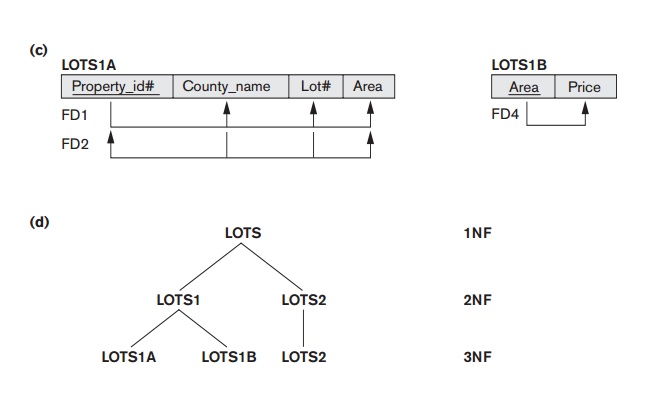
According to this definition, LOTS2 (Figure 15.12(b)) is in 3NF. However, FD4 in LOTS1 violates 3NF because Area is not a superkey and Price is not a prime attribute in LOTS1. To normalize LOTS1 into 3NF, we decompose it into the relation schemas LOTS1A and LOTS1B shown in Figure 15.12(c). We construct LOTS1A by removing the attribute Price that violates 3NF from LOTS1 and placing it with Area (the left-hand side of FD4 that causes the transitive dependency) into another relation

LOTS1B. Both LOTS1A and LOTS1B are in 3NF.

Two points are worth noting about this example and the general definition of 3NF:

■                             LOTS1 violates 3NF because Price is transitively dependent on each of the candidate keys of LOTS1 via the nonprime attribute Area.

        This general definition can be applied directly to test whether a relation schema is in 3NF; it does not have to go through 2NF first. If we apply the above 3NF definition to LOTS with the dependencies FD1 through FD4, we find that both FD3 and FD4 violate 3NF. Therefore, we could decompose LOTS into LOTS1A, LOTS1B, and LOTS2 directly. Hence, the transitive and

partial dependencies that violate 3NF can be removed in any order.

3. Interpreting the General Definition of Third Normal Form

A relation schema R violates the general definition of 3NF if a functional dependency X → A holds in R that does not meet either condition—meaning that it violates both conditions (a) and (b) of 3NF. This can occur due to two types of problematic functional dependencies:

        A nonprime attribute determines another nonprime attribute. Here we typically have a transitive dependency that violates 3NF.

        A proper subset of a key of R functionally determines a nonprime attribute. Here we have a partial dependency that violates 3NF (and also 2NF).

Therefore, we can state a general alternative definition of 3NF as follows:

Alternative Definition. A relation schema R is in 3NF if every nonprime attribute of R meets both of the following conditions:

        It is fully functionally dependent on every key of R.

It is nontransitively dependent on every key of R.