Equation of Motion

EQUATION OF MOTION

There is two types of equation of motion

Longitudinal vibration of beam or axial vibration of a rod

Transverse vibration of a beam

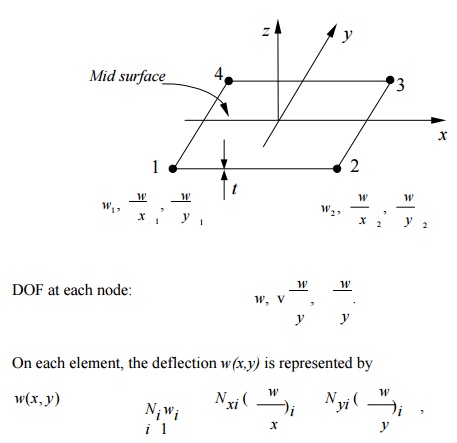
where Ni, Nxi and Nyi are shape functions. This is an incompatible element! The stiffness matrix is still of the form

k =   BTEBdV ,

where B is the strain-displacement matrix, and E the stress- strain matrix.

Minding Plate Elements:

4-Node Quadrilateral

8-Node Quadrilateral

Three independent fields.

Deflection w(x,y) is linear for Q4, and quadratic for Q8.

Discrete Kirchhoff Element:

Triangular plate element (not available in ANSYS). Start with a 6-node riangular element,

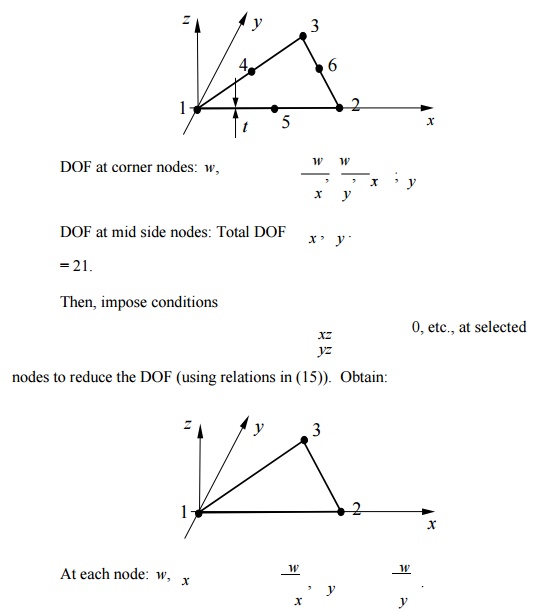
Total DOF = 9  (DKT Element).

Incompatible w(x,y);  convergence is faster (w is cubic along each edge) and it is efficient.

Test Problem:

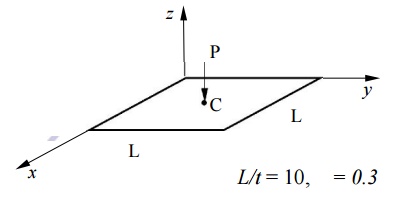
L/t = 10,   = 0.3

ANSYS 4-node quadrilateral plate element.

ANSYS Result for wc

Mesh           wc (  PL2/D)

2        2                           0.00593

4        4                           0.00598

8        8                           0.00574

16      16                         0.00565

          :                            :

Exact Solution                         0.00560

Question:Converges from “above”? Contradiction to what we learnt about the nature of the FEA solution?

Reason:  This is an incompatible element ( See comments on p. 177).

Shells and Shell Elements

Shells – Thin structures witch span over curved surfaces.

Example:

Sea shell, egg shell (the wonder of the nature); Containers, pipes, tanks; Car bodies;

Roofs, buildings (the Superdome), etc. Forces in shells:

Membrane forces + Bending Moments

(cf.  plates:  bending only)

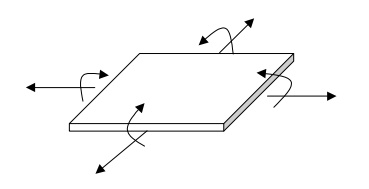
Example: A Cylindrical Container.

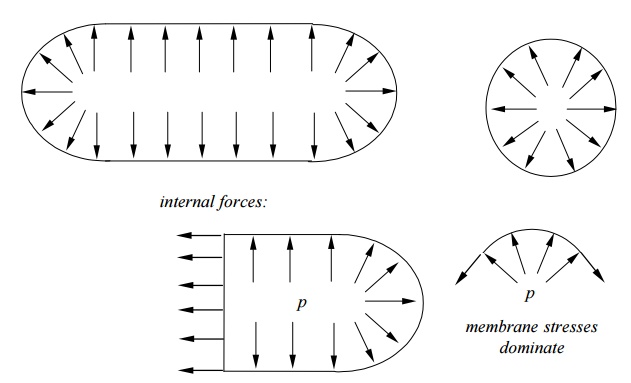
Shell Theory:

Thin shell theory

Shell theories are the most complicated ones to formulate and analyze in mechanics (Russian’s contributions).

Engineering Craftsmanship Demand strong analytical skill

Shell Elements:

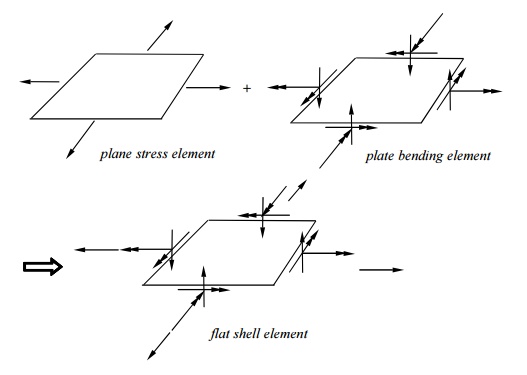
cf.: bar + simple beam element => general beam element.

DOF at each node:

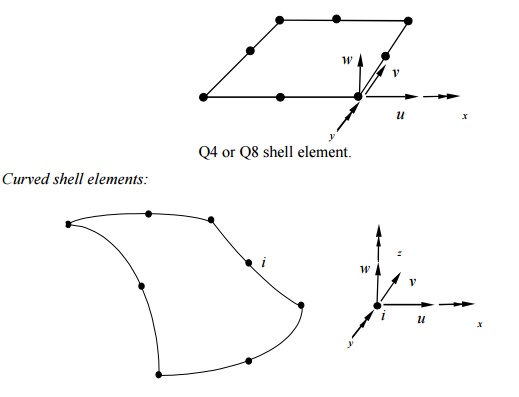
Based on shell theori es;

Most general shell el ements (flat shell and plate elements are subsets);

Complicated in form ulation.

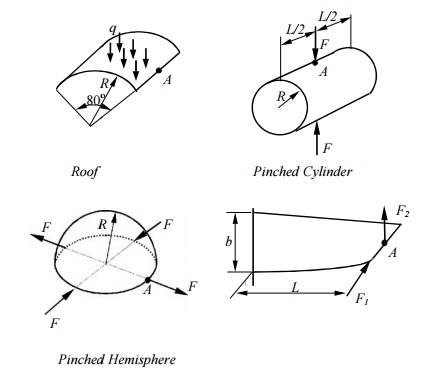
Test Cases: