Worked out Problems: Depreciation

WORKEDOUT PROBLEMS

Single-Payment Compound Amount

A person deposits a sum of Rs. 20,000 at the interest rate of 18% compounded annually for 10 years. Find the maturity value after 10 years.

Solution

P = Rs. 20,000

i = 18% compounded annually n = 10 years

F  = P(1 + i)ⁿ = P(F/P, i, n)

=  20,000 (F/P, 18%, 10)

=  20,000    5.234 = Rs. 1,04,680

The maturity value of Rs. 20,000 invested now at 18% compounded yearly is equal to Rs. 1,04,680 after 10 years.

Single-Payment Present Worth Amount

A person wishes to have a future sum of Rs. 1,00,000 for his son’s education after 10 years from now. What is the single-payment that he should deposit now so that he gets the desired amount after 10 years? The bank gives 15% interest rate compounded annually.

Solution

F = Rs. 1,00,000

i = 15%, compounded annually n = 10 years

P  = F/(1 + i)ⁿ  = F(P/F, i, n)

= 1,00,000 (P/F, 15%, 10

= 1,00,000 0.2472

= Rs. 24,720

The  person  has  to invest  Rs.  24,720  now  so  that  he  will  get  a  sum  of Rs. 1,00,000 after 10 years at 15% interest rate compounded annually

Equal-Payment Series Sinking Fund

A company has to replace a present facility after 15 years at an outlay of Rs. 5,00,000. It plans to deposit an equal amount at the end of every year for the next 15 years at an interest rate of 18% compounded annually. Find the equivalent amount that must be deposited at the end of every year for the next 15 years.

Solution

F = Rs. 5,00,000 n = 15 years

i = 18% A = ?

The corresponding cash flow diagram is shown in Fig.

Fig.  Cash flow diagram of equal-payment series sinking fund.

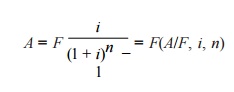
= 5,00,000(A/F, 18%, 15) = 5,00,000 0.0164 = Rs. 8,200

The annual equal amount which must be deposited for 15 years is Rs. 8,200.

Equal-Payment Series Present Worth Amount

A company wants to set up a reserve which will help the company to have an annual equivalent amount of Rs. 10,00,000 for the next 20 years towards its employees welfare measures. The reserve is assumed to grow at the rate of 15% annually. Find the single-payment that must be made now as the reserve amount.

Solution

A = Rs. 10,00,000 i = 15%

n = 20 years P = ?

The corresponding cash flow diagram is illustrated in Fig.

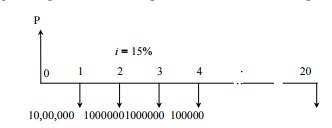
Fig.   Cash flow diagram of equal-payment series present worth amount.

The formula to compute P is

The amount of reserve which must be set-up now is equal to Rs. 62,59,300.

Equal-Payment Series Capital Recovery Amount

A bank gives a loan to a company to purchase an equipment worth Rs. 10,00,000 at an interest rate of 18% compounded annually. This amount should be repaid in 15 yearly equal installments. Find the installment amount that the company has to pay to the bank.

Solution

P = Rs. 10,00,000 i = 18%

n = 15 years A = ?

The corresponding cash flow diagram is shown in Fig..

The annual equivalent installment to be paid by the company to the bank is Rs. 1,96,400.

Uniform Gradient Series Annual Equivalent Amount

A person is planning for his retired life. He has 10 more years of service. He would like to deposit 20% of his salary, which is Rs. 4,000, at the end of the first year, and thereafter he wishes to deposit the amount with an annual increase of Rs. 500 for the next 9 years with an interest rate of 15%. Find the total amount at the end of the 10th year of the above series.

Solution

Here,

A1 = Rs. 4,000

G = Rs. 500

i = 15%

n = 10 years

A = ? & F = ?

The cash flow diagram is shown in Fig.

Fig. Cash flow diagram of uniform gradient series annual equivalent amount.

This is equivalent to paying an equivalent amount of Rs. 5,691.60 at the end of every year for the next 10 years. The future worth sum of this revised series at the end of the 10th year is obtained as follows:

F= A(F/A, i, n)

=  A(F/A, 15%, 10)

=   5,691.60(20.304)

=  Rs. 1,15,562.25

At the end of the 10th year, the compound amount of all his payments will be Rs. 1,15,562.25

Effective Interest Rate

A person invests a sum of Rs. 5,000 in a bank at a nominal interest rate of 12% for 10 years. The compounding is quarterly. Find the maturity amount of the deposit after 10 years.

Solution

P = Rs. 5,000 n = 10 years

i = 12% (Nominal interest rate) F = ?

METHOD 1

No. of interest periods per year = 4

No. of interest periods in 10 years = 10 4 = 40 Revised No. of periods (No. of quarters), N = 40 Interest rate per quarter, r = 12%/4

= 3%, compounded quarterly.

F    = P(1 + r)^N  = 5,000(1 + 0.03)⁴⁰

=  Rs. 16,310.19

METHOD 2

No. of interest periods per year, C = 4

Effective interest rate, R  = (1 + i/C )^C  – 1

=  (1 + 12%/4)⁴  – 1

=  12.55%, compounded annually.

F    = P(1 + R)ⁿ  = 5,000(1 + 0.1255)¹⁰

= Rs. 16,308.91