Chapter: Mechanical : Engineering Economics & Cost Analysis : Depreciation
Methods of Depreciation
Methods of Depreciation
There are several methods of accounting depreciation fund. These are as follows:
1. Straight line method of depreciation
2. Declining balance method of depreciation
3. Sum of the years—digits method of depreciation
4. Sinking-fund method of depreciation
5. Service output method of depreciation
1.Straight Line Method of Depreciation
In this method of depreciation, a fixed sum is charged as the depreciation amount throughout the lifetime of an asset such that the accumulated sum at the end of the life of the asset is exactly equal to the purchase value of the asset.
Here, we make an important assumption that inflation is absent.
Let
P = first cost of the asset,
F = salvage value of the asset
n = life of the asset,
Bt = book value of the asset at the end of the period t,
Dt = depreciation amount for the period t.
The formulae for depreciation and book value are as follows:
Dt = (P – F)/n
Bt = Bt–1 – Dt = P – t [(P – F)/n]
EXAMPLE
A company has purchased an equipment whose first cost is Rs. 1,00,000 with an estimated life of eight years. The estimated salvage value of the equipment at the end of its lifetime is Rs. 20,000. Determine the depreciation charge and book value at the end of various years using the straight line method of depreciation.
Solution
P = Rs. 1,00,000 F = Rs. 20,000 n = 8 years
Dt = (P – F)/n
= (1,00,000 – 20,000)/8
= Rs. 10,000
In this method of depreciation, the value of Dt is the same for all the years. The calculations pertaining to Bt for different values of t are summarized in Table .
Table Dt and Bt Values under Straight line Method of Depreciation
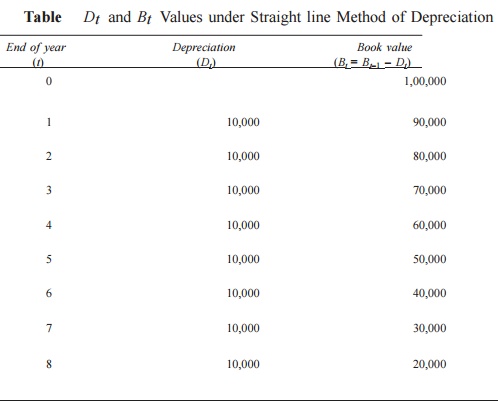
If we are interested in computing Dt and Bt for a specific period (t), In the formulae can be used. this approach, it should be noted that the all the depreciation is the same for periods.
EXAMPLE
Consider Example and compute the depreciation and the book value for period 5.
P = Rs. 1,00,000
F = Rs. 20,000 n = 8 years
D5 = (P – F)/n
= (1,00,000 – 20,000)/8
= Rs. 10,000 (This is independent of the time period.)
Bt = P – t (P – F)/n
B5 = 1,00,000 – 5 (1,00,000 – 20,000)/8
= Rs. 50,000
2.Declining Balance Method of Depreciation
ü In this method of depreciation, a constant percentage of the book value of the previous period of the asset will be charged as the depreciation amount for the current period.
ü This approach is a more realistic approach, since the depreciation charge decreases with the life of the asset which matches with the earning potential of the asset.
ü The book value at the end of the life of the asset may not be exactly equal to the salvage value of the asset. This is a major limitation of this approach.
Let
P = first cost of the asset,
F = salvage value of the asset,
n = life of the asset,
Bt = book value of the asset at the end of the period t,
K = a fixed percentage, and
Dt = depreciation amount at the end of the period t.
The formulae for depreciation and book value are as follows:
Dt = K Bt-1
Bt = Bt–1 – Dt = Bt–1 – K Bt–1
= (1 – K) Bt–1
The formulae for depreciation and book value in terms of P are as follows:
Dt = K(1 – K)t–1
P Bt = (1 – K)t
P
While availing income-tax exception for the depreciation amount paid in each year, the rate K is limited to at the most 2/n. If this rate is used, then the corresponding approach is called the double declining balance method of depreciation.
EXAMPLE
Consider Example 9.1 and demonstrate the calculations of the declining balance method of depreciation by assuming 0.2 for K.
Solution
P = Rs. 1,00,000
F = Rs. 20,000
n = 8 years
K = 0.2
The calculations pertaining to Dt and Bt for different values of t
are summarized in Table 9.2 using the following formulae:
Dt = K Bt–1
Bt = Bt–1 – Dt
Table Dt and Bt according to Declining Balance Method of Depreciation
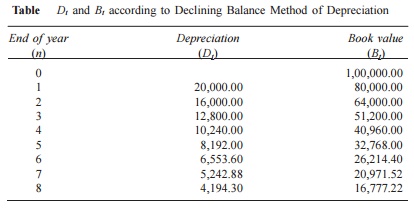
If we are interested in computing Dt and Bt for a specific period t, the respective formulae can be used.
EXAMPLE Consider Example 9.1 and calculate the depreciation and the book value for period 5 using the declining balance method of depreciation by assuming 0.2 for K.
Solution
P = Rs. 1,00,000
F = Rs. 20,000
n = 8 years
K = 0.2

= Rs. 32,768
3.Sum-of-the-Years-Digits Method of Depreciation
In this method of depreciation also, it is assumed that the book value of the asset decreases at a decreasing rate. If the asset has a life of eight years, first the sum of the years is computed as
Sum of the years = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36 = n(n + 1)/2
The rate of depreciation charge for the first year is assumed as the highest and then it decreases. The rates of depreciation for the years 1–8, respectively are as follows: 8/36, 7/36, 6/36, 5/36, 4/36, 3/36, 2/36, and 1/36.
For any year, the depreciation is calculated by multiplying the corresponding rate of depreciation with (P – F).
Dt = Rate (P – F)
Bt = Bt–1 – Dt
The formulae for Dt and Bt for a specific year t are as follows:
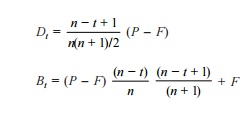
EXAMPLE
Consider Example 9.1 and demonstrate the calculations of the sum-of-the-years-digits method of depreciation.
Solution
P = Rs.
1,00,000
F = Rs.
20,000 Sum = n (n + 1)/2 = 8 9/2 = 36
n = 8 years
The rates for years 1–8, are respectively 8/36, 7/36, 6/36, 5/36, 4/36, 3/36,2/36 and 1/36.
The calculations of Dt and Bt for different values of t are summarized in
Table using the following formulae:
Dt = Rate (P – F)
Bt = Bt–1 – Dt
Table Dt and Bt under Sum-of-the-years-digits Method of Depreciation
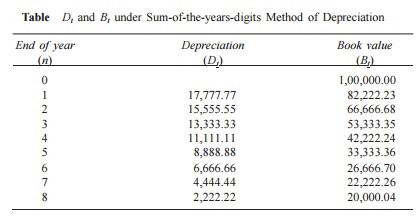
If we are interested in calculating Dt and Bt for a specific t, then the usage of the formulae would be better.
EXAMPLE 9.6 Consider Example 9.1 and find the depreciation and book value for the 5th year using the sum-of-the-years-digits method of depreciation.
Solution
P = Rs. 1,00,000
F = Rs. 20,000
n = 8 years

4. Sinking Fund Method of Depreciation
In this method of depreciation, the book value decreases at increasing rates with respect to the life of the asset
Let
P = first cost of the asset,
F = salvage value of the asset, n = life of the asset,
i = rate of return compounded annually,
A = the annual equivalent amount,
Bt = the book value of the asset at the end of the period t, and
Dt = the depreciation amount at the end of the period t.
The loss in value of the asset (P – F) is made available an the form of cumulative depreciation amount at the end of the life of the asset by setting up an equal depreciation amount (A) at the end of each period during the lifetime of the asset.
A = (P – F) [A/F, i, n]
The fixed sum depreciated at the end of every time period earns an interest at the rate of i% compounded annually, and hence the actual depreciation amount will be in the increasing manner with respect to the time period. A generalized formula for Dt is
Dt = (P – F) (A/F, i, n) (F/P, i, t – 1) The formula to calculate the book value at the end of period t is
Bt = P – (P – F) (A/F, i, n) (F/A, i, t)
The above two formulae are very useful if we have to calculate Dt and Bt for any specific period.
If we calculate Dt and Bt for all the periods, then the tabular approach would be better.
EXAMPLE
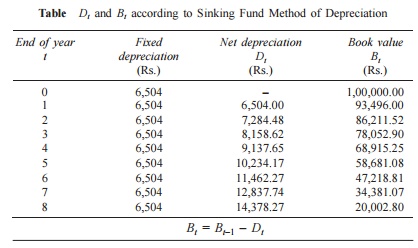
Consider Example and give the calculations regarding the sinking fund method of depreciation with an interest rate of 12%, compounded annually.

In this method of depreciation, a fixed amount of Rs. 6,504 will be depreciated at the end of every year from the earning of the asset.
The depreciated amount will earn interest for the remaining period of life of the asset at an interest rate of 12%, compounded annually.
For example, the calculations of net depreciation for some periods are as follows:
Depreciation at the end of year 1 (D1) = Rs. 6,504.
Depreciation at the end of year 2 (D2) = 6,504 + 6,504 0.12 = Rs. 7,284.48
Depreciation at the end of the year 3 (D3)
= 6,504 + (6,504 + 7,284.48) .12
= Rs. 8,158.62
Depreciation at the end of year 4 (D4)
= 6,504 + (6,504 + 7,284.48 + 8,158.62) 0.12 = Rs. 9,137.65
These calculations along with book values are summarized in Table .
Table Dt and Bt according to Sinking Fund Method of Depreciation
EXAMPLE
Consider Example and compute D5 and B7 using the sinking fund method of depreciation with an interest rate of 12%, compounded annually.
Solution
P = Rs. 1,00,000
F = Rs. 20,000 n = 8 years
i = 12%
Dt = (P – F) (A/F, i, n) (F/P, i, t – 1)
D5 = (P – F) (A/F, 12%, 8) (F/P, 12%, 4)
= (1,00,000 – 20,000) 0.0813 1.574
= Rs. 10,237.30
This is almost the same as the corresponding value given in the table. The minor difference is due to truncation error.
Bt = P – (P – F) (A/F, i, n) (F/A, i, t)
B7 = P – (P – F) (A/F, 12%, 8) (F/A, 12%, 7)
= 1,00,000 – (1,00,000 – 20,000) 0.0813 10.089
= 34,381.10
5. Service Output Method of Depreciation
In some situations, it may not be realistic to compute depreciation based on time period. In such cases, the depreciation is computed based on service rendered by an asset. Let
P = first cost of the asset
F = salvage value of the asset
X = maximum capacity of service of the asset during its lifetime
x = quantity of service rendered in a period.
Then, the depreciation is defined per unit of service rendered: Depreciation/unit of service = (P – F)/X
Depreciation for x units of service in a period = P-F(x)/X
EXAMPLE
The first coat of a road laying machine is Rs. 80,00,000. Its salvage value after five years is Rs. 50,000. The length of road that can be laid by the machine during its lifetime is 75,000 km. In its third year of operation, the length of road laid is 2,000 km. Find the depreciation of the equipment for that year.
Solution
P = Rs. 80,00,000
F = Rs. 50,000
X = 75,000 km

Related Topics