Weighted Index Numbers

METHODS OF CONSTRUCTING INDEX NUMBERS

Different types of index number (price/quantity/value) can be classified as follows.

WEIGHTED INDEX NUMBERS

In computing weighted Index Numbers, the weights are assigned to the items to bring out their economic importance. Generally quanties consumed or value are used as weights.

Weighted index numbers are also of two types

(i) Weighted aggregative

(ii) Weighted average of price relatives

1. Weighted aggregate Index Numbers

In this method price of each commodity is weighted by the quantity sale either in the base year or in the current year. There are various methods of assigning weights and thus there are many methods of constructing index numbers. Some of the important formulae used under this methods are

a) Laspeyre’s Index (P₀₁^L)

b) Paasche’s Index (P₀₁^P)

c) Dorbish and Bowley’s Index (P₀₁^DB)

d) Fisher’s Ideal Index (P₀₁^F)

e) Marshall-Edgeworth Index (P₀₁^Em)

f) Kelly’s Index (P₀₁^K)

a. Laspeyre’s method

The base period quantities are taken as weights. The Index is

b. Paasche’s method

The current year quantities are taken as a weight. In this method, we use continuously revised weights and thus this method is not frequently used when the number of commodities is large. The Index is

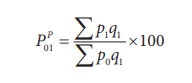
c. Dorbish and Bowley’s method

In order in take into account the impact of both the base and current year, we make use of simple arithmetic mean of Laspeyre’s and Paasche’s formula

The Index is

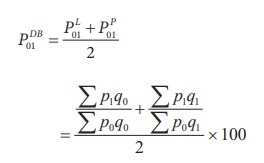
d. Fisher’s Ideal Index

It is the geometric mean of Laspeyre’s Index and Paasche’s Index, given by:

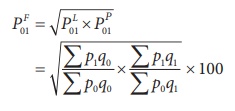
e. Marshall-Edgeworth method

In this method also both the current year as well as base year prices and quantities are considered.

The Index is

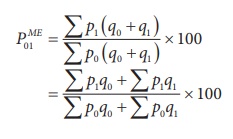
f. Kelly’s method

The Kelly’s Index is

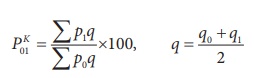
where q refers to quantity of some period, not necessarily of the mean of the base year and current year. It is also possible to use average quantity of two or more years as weights. This method is known as fixed weight aggregative index.

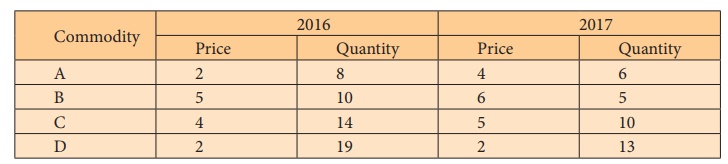
Example 6.6

Construct weighted aggregate index numbers of price from the following data by applying

1. Laspeyre’s method

2. Paasche’s method

3. Dorbish and Bowley’s method

4. Fisher’s ideal method

5. Marshall-Edgeworth method

Solution:

Calculation of various indices

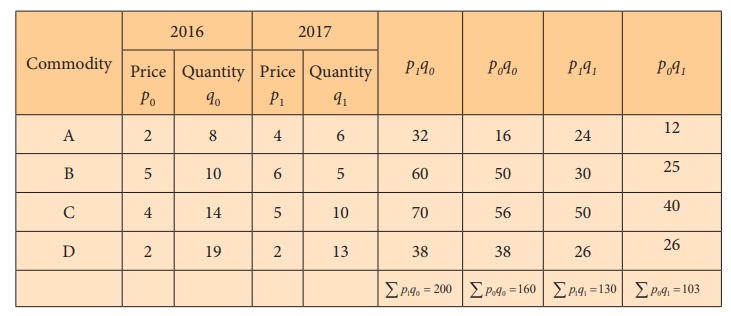
(1) Laspeyre’s Index:

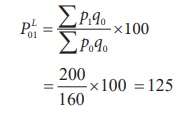
(2) Paasche’s Index

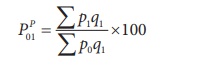
= 130 / 103 ×100 = 126.21

(3) Dorbish and Bowley’s Index

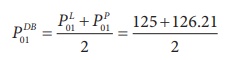
= 125.6 

(4) Fisher’s Ideal Index

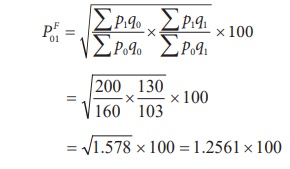
= 125.61

(5) Marshall-Edgeworth method

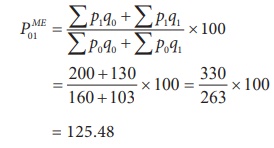
= 125.48

Example 6.7

Calculate the price indices from the following data by applying (1) Laspeyre’s method (2) Paasche’s method and (3) Fisher ideal number by taking 2010 as the base year.

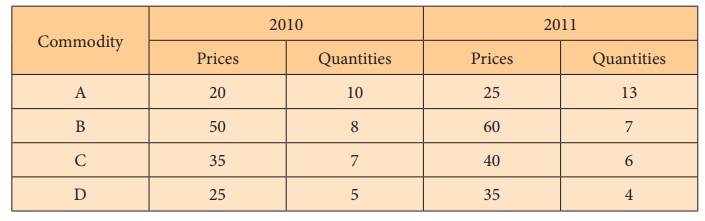
Solution: Calculations

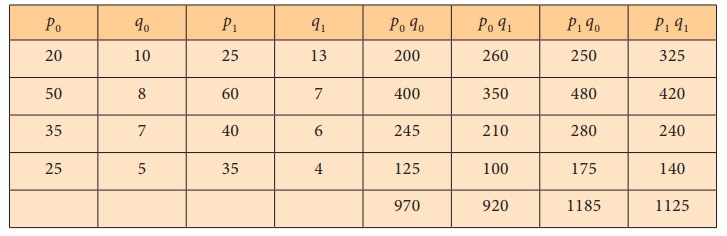
(1) Laspeyre’s Index

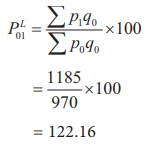
(2) Paasche’s Index

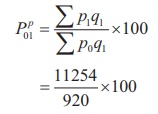
= 122.28

(3) Fisher’s Ideal Index

= 1.2055×100

= 120.55

Example 6.8

Calculate the Dorbish and Bowley’s price index number for the following data taking 2014 as base year.

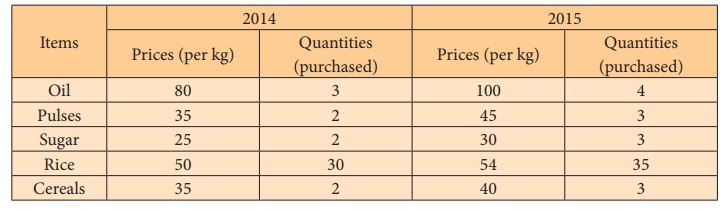
Solution: Price Index by Dorbish and Bowley’s Method

= 1.1164 x 100 = 111.64

Example 6.9

Compute Marshall – Edgeworth price index number for the following data by taking 2016 as base year.

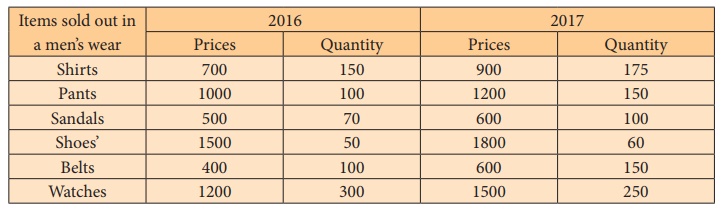
Solution: Price Index by Marshall-Edgeworth Method

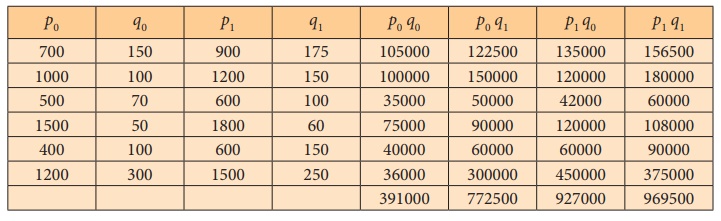
Marshall – Edgeworth Index:

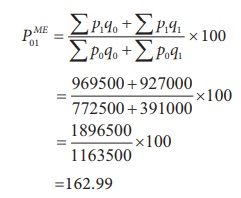
Example 6.10

Calculate a suitable price index form the following data.

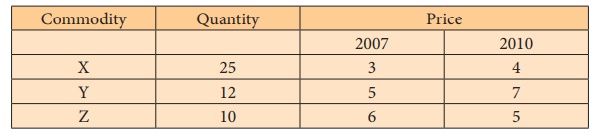
Solution:

In this problem, the quantities for both current year and base year are same. Hence, we can conlude Kelly’s Index price number.

Kelly’s price Index number:

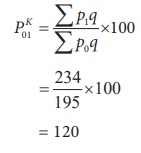
= 120

2. Weighted average of price relatives

The weighted average of price relatives can be computed by introducing weights into the unweighted price relatives. Here also, we may use either arithmetic mean or the geometric mean for the purpose of averaging weighted price relatives.

The weighted average price relatives using arithmetic mean:

If p = [p₁/ p₀] × 100 is the price relative index and w = p₀q₀ is attached to the commodity, then  the weighed price relative index is 

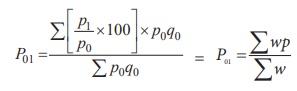
The weighted average price relatives using geometric mean:

Example 6.11

Compute price index for the following data by applying weighted average of price relatives method using (i) Arithmetic mean and (ii) Geometric mean.

Solution:

(i) Computation for the weighted average of price relatives using arithmatic mean.

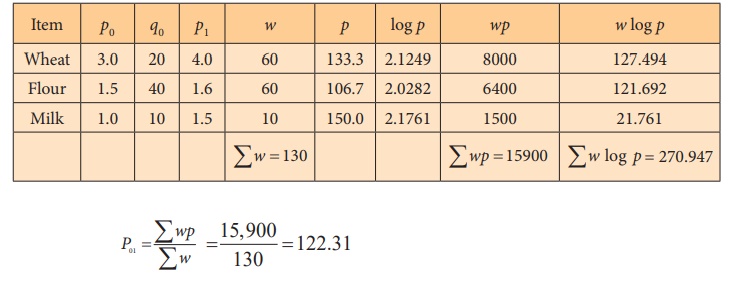
This means that there has been a 22.31 % increase in prices over the base year.

(ii) Index number using geometric mean of price relatives is:

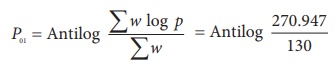
= Antilog (2.084) = 121.3

This means that there has been a 21.3 % increase in prices over the base year.

3. Quantity Index Number

The quantity index number measures the changes in the level of quantities of items consumed, or produced, or distributed during a year under study with reference to another year known as the base year.

These formulae represent the quantity index in which quantities of the different commodities are weighted by their prices.

Example 6.12

Compute the following quantity indices from the data given below:

(i) Laspeyre’s quantity index (ii) Paasche’s quantity index and (iii) Fisher’s quantity index

Solution:

Since we are given the value and the prices, the quantity figures can be obtained by dividing the value by the price for each of the commodities.

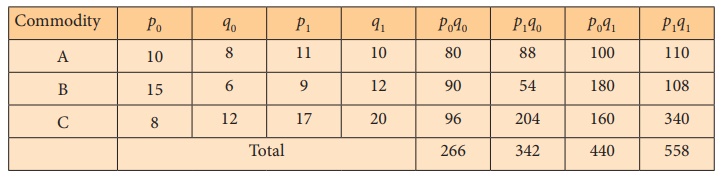
(i) Laspeyre’s quantity index

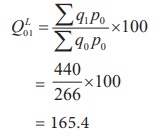
(ii) Paasche’s quantity index

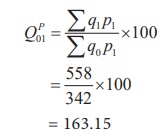
(iii) Fisher’s quantity index

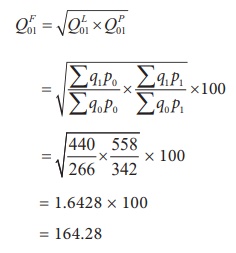
4. Tests for Index numbers

Fisher has given some criteria that a good index number has to satisfy. They are called (i) Time reversal test (ii) Factor reversal test (iii) Circular test. Fisher has constructed in such a way that this index number satisfies all these tests and hence it is called Fisher’s Ideal Index number.

Time reversal test

Fisher has pointed out that a formula for an index number should maintain time consistency by working both forward and backward with respect to time. This is called time reversal test. Fisher describes this test as follows.

“The test is that the formula for calculating an index number should be such that it gives the same ratio between one point of comparison and the other, no matter which of the two is taken as base or putting in another way the index number reckoned forward should be the reciprocal of that reckoned back ward”. A good index number shoud satisfy the time reversal test.

This statement is expressed in the form of equation as P₀₁ × P₁₀ = 1.

Where

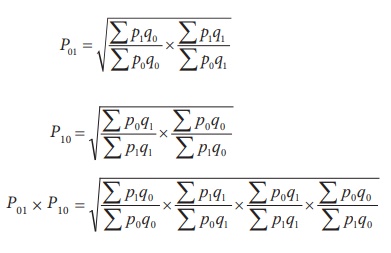
Hence, P₀₁ × P₁₀ = √1 = 1

Factor reversal test

This test is also suggested by Fisher According to the factor reversal test, the product of price index and quantity index should be equal to the corresponding value index.

In Fisher’s words “Just as each formula should permit the interchange of two times without giving inconsistent results so it ought to permit interchanging the prices and quantities without giving inconsistent results. i.e, the two results multiplied together should give the true ratio”.

This statement is expressed as follows:

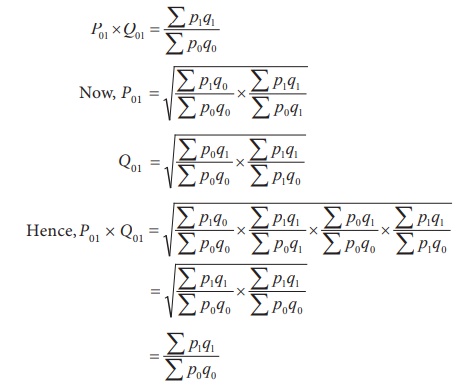
Circular Test

It is an extension of time reversal test. The time reversal test takes into account only two years. The current and base years. The circular test would require this property to holdgood for any two years. An index number is said to satisfy the circular test when there are three indices, P₀₁, P₁₂ and P₂₀, such that P₀₁ × P₁₂ × P₂₀ = 1.

Laspeyres, Paasche’s and Fisher’s ideal index numbers do not satisfy this test.

Example 6.13

The table below gives the prices of base year and current year of 5 commodities with their quantities. Use it to verify whether Fisher’s ideal index satisfies time reversal test.

Solution:

Index number by Fisher’s ideal index method

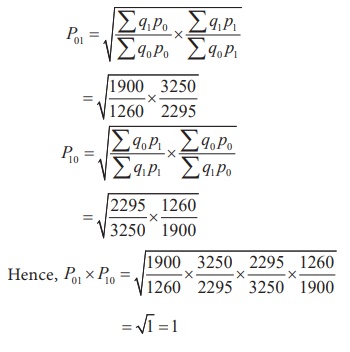
Fisher’s Index number satisties time reveral test.

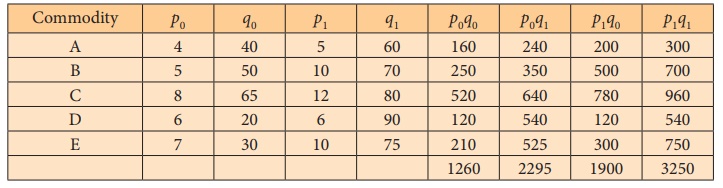
Example 6.14

Calculate the price index and quantity index for the following data by Fisher’s ideal formula and verify that it statisfies the factor reversal test.

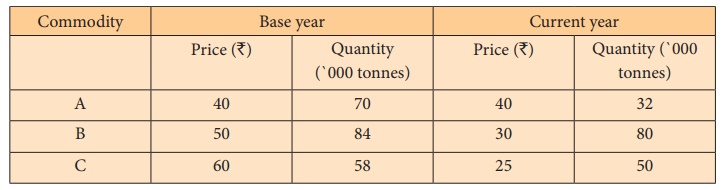
Solution

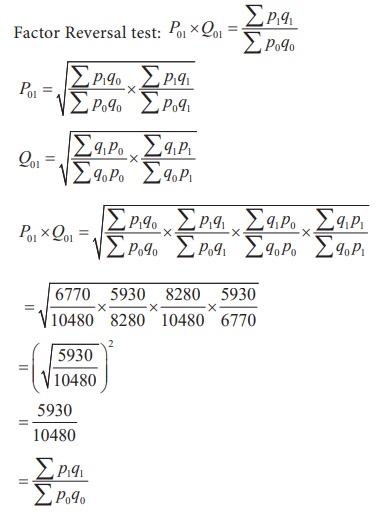
Hence, Fisher ideal index number satisfies the factor reversal test