Unweighted Index Numbers

METHODS OF CONSTRUCTING INDEX NUMBERS

Different types of index number (price/quantity/value) can be classified as follows.

Unweighted Index Numbers

An unweighted price Index Number measures the percentage change in price of a single item or a group of items between two periods of time. In unweighted index numbers, all the values taken for study are of equal importance. There are two methods in this category.

(i) Simple aggregative method:

Under this method the prices of different items of current year are added and the total is divided by the sum of prices of the base year items and multiplied by 100.

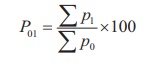
p₁ = Current year prices for various commodities

p₀ = Base year prices for various commodities

P₀₁ = Price Index number

Limitations of the simple aggregative method

(i) Relative importance of the commodities is not taken into account.

(ii) Highly priced items influence the index number

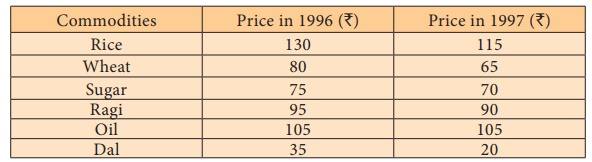
Example 6.1

Construct the Price Index Number for the year 1997, from the following information taking 1996 as base year.

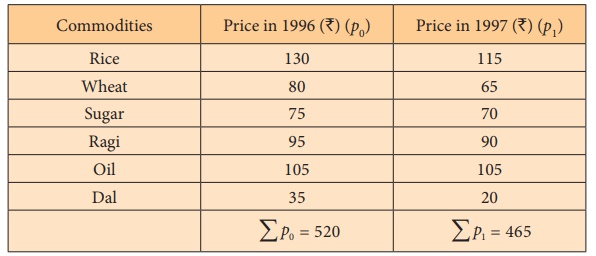
Solution:

Construction of Price Index:

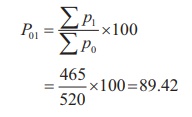
Price Index in 1997, when compared to 1996 has fallen by 10.58%

Example 6.2

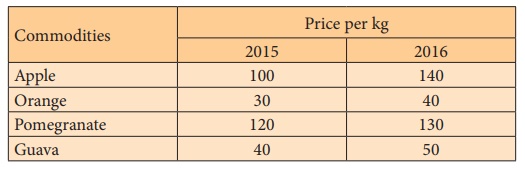
Calculate Price Index Number for 2016 from the following data by simple aggregate method, taking 2016 as base year.

Solution:

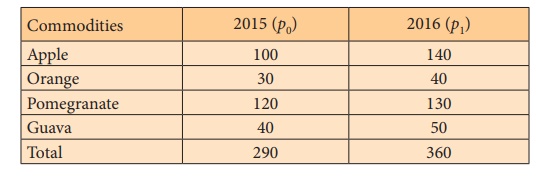
= 3600/29

P₀₁ = 124.13%

Price index for the year 2016 when compared to 2015 has been increased by 24.13%.

2. Simple average of price relative method

Under this method, first of all price relatives are obtained for the various items and then average of these relatives is obtained by using either arithmetic mean or geometric mean. Price relative is the price of the current year expressed as the percentage of the price of the base year. The formula for computing Index Number under this method on using Arithmetic mean and Geometric mean are given below.

If N is the member of items, p₁ is the price of the commodity with current year and p₀ is the price of the commodity in the base year then, the average Price Index Number is

Advantages of Average Price Index

1. It is not influenced by the extreme prices of items as equal importance is given to all items.

2. Price relatives are pure numbers; therefore the value of the average price relative index is not affected by the units of measurement of commodities included in the calculation of index numbers.

Limitations

1. Equal weights are assigned to every commodity included in the index. Each price relatives is given equal importance, but in actual practice, it is not true.

2. Arithmetic mean is very often used to calculate the average price relatives, but it has a few disadvantages. The use of geometric mean is difficult to calculate.

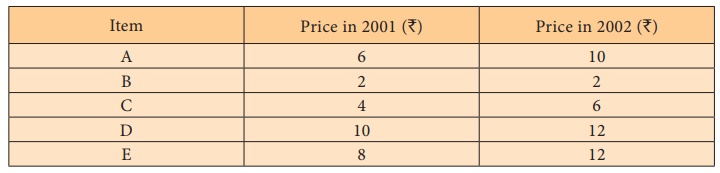
Example 6.3

Compute price index number by simple average of price relatives method using arithmetic mean and geometric mean.

Solution:

Calculation of price index number by simple average of price relatives:

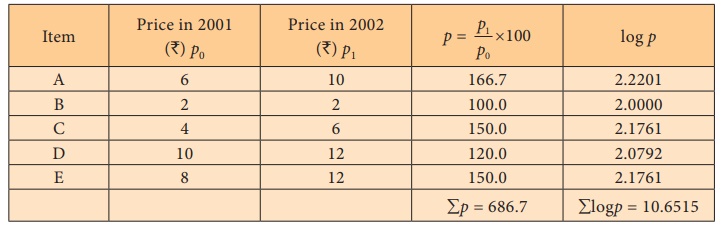
(i) Price relative index number based on arithmetic mean:

(ii) Price relative index number based on geometric mean:

= antilog (2.13303)

= 134.9

Hence, the price index number based on arithmetic mean and geometric mean for the year 2002 are 137.34 and 134.9 respectively.

Example 6.4

Construct simple average price relative index number using arithmetic mean for the year 2012 for the following data showing the profit from various categories sold out in departmental stores.

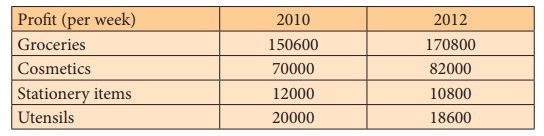
Solution: 

Index number uning Arithmertic Mean of price relatives

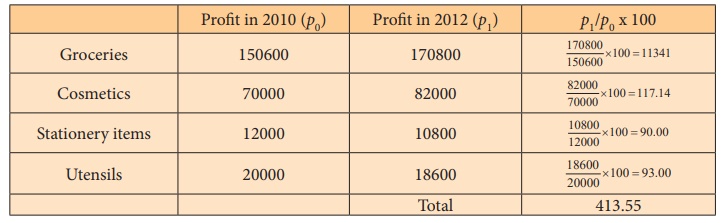
Simple average price relatives using A.M =

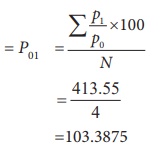
=103.3875

P₀₁ = 103.39

The average price relative index number using arithmetic mean for the year 2012 is 103.39

Example 6.5

Construct simple average price relative index number using geometric mean for the year 2015 for the data showing the expenditure in education of the children taking different courses.

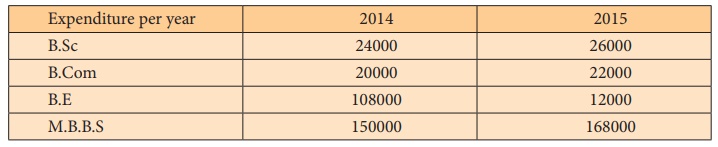
Solution:

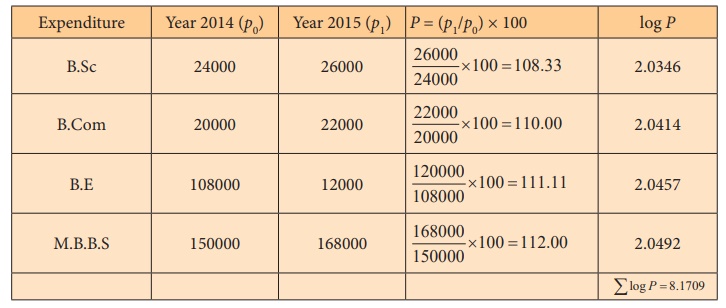
P₀₁ = antilog (∑ log P / N )

= antilog ( 8.1709 / 4)

= antilog (2.04275)

= antilog (2.0428)

 = 110.4

The average price relative index number using geometric mean for the year 2015 is 110.4