Chapter: Mathematics (maths) : Vector Calculus
Vector Calculus
VECTOR CALCULUS
1 Gradient-Directional Derivative
2. Divergence And Curl –Irrotational And Solenoidal Vector Fields
Divergence
3 Vector Integration
4 Green’s Theorem In
A Plane;(Excluding proof)
5 Gauss Divergence Theorem:(Excluding proof)
6 Stoke’s
Theorem(Excluding proof)
VECTOR CALCULUS
1Gradient-Directional
Derivative
1.1. Gradient
1(a) The Vector Differential
Operator

1(b) The Gradient (Or Slope Of A Scalar Point
Function)


1.2. Directional
Derivative
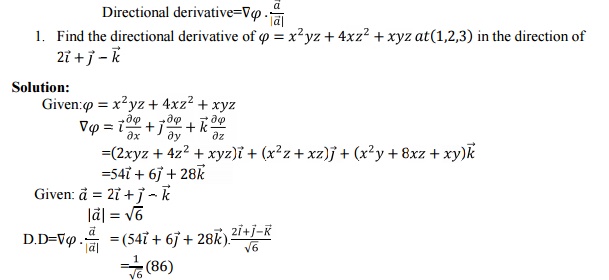
1.3. Unit Tangent Vector
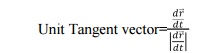
1.Find a
unit tangent vector to the following surfaces at the specified

1.4 Normal Derivative

1.5 Unit Normal Vector

1.6 Angle Between The Suraces

1.7 .Scalar Potential

1. 8 The Vector Equation of the Tangent Plane And Normal Line to the Surface
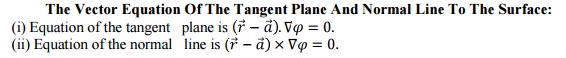
Tutorial Problems:
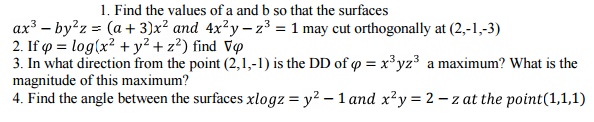
2 Divergence And Curl –Irotational
And Solenoidal Vector Fields:
2.1 Divergence and curl
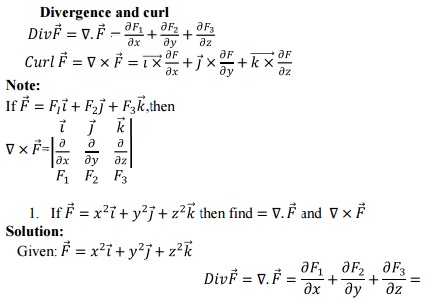


2.2 SOLENOIDAL VECTOR,IRROTATIONAL VECTOR:
Solenoidal vector formula:



Laplace Operator:
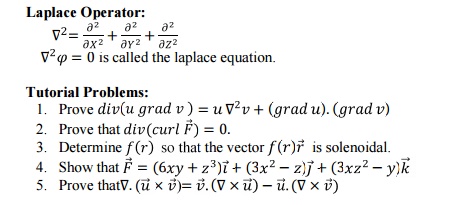
3 Vector Integration
Conservative Vector Field:

3.1. Line Integral:

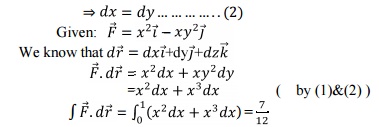
3.2. Surface Integral:
Definition: Consider a
surface S .Let n denote the unit outward normal to the surface S. Let R be the
projection of the surface x on xy plane. Let Vec f be a vector function defined
in some region containing the surface S,
then the surface integral of Vector f is defined to be

3.3. Volume Integral:
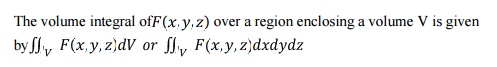
3.4 Tutorial Problems:

4 .Green’s Theorem In
A Plane:
Statement:


Tutorial Problems:
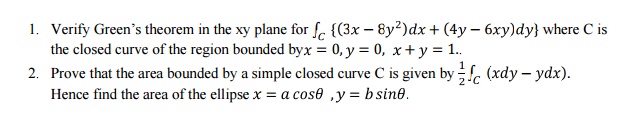
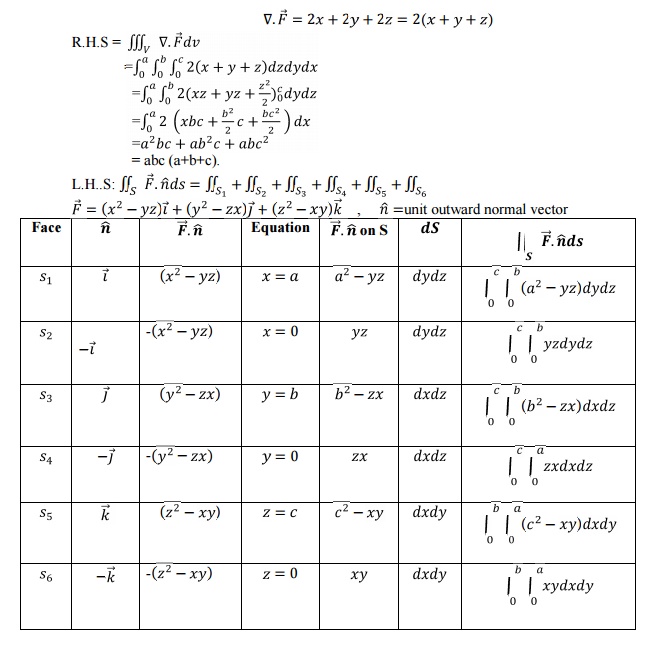
5 Gauss Divergence Theorem:
Statement:
The surface integral of the normal
component of a vector function F over a closed surface S enclosing volume V is equal to the volume
integral of the divergence of F
taken throughout the

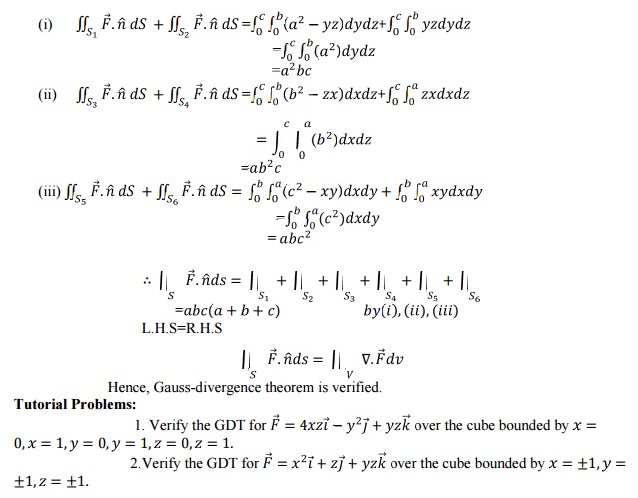
6. Stoke’s Theorem
Statement:
The
surface integral of the normal component of the curl of a vector function F
over an open surface S is equal to the line integral of the tangential
component of F around the closed curve C bounding S.


Hence, Stoke’s theorem is verified.
6.1 Tutorial Problems:
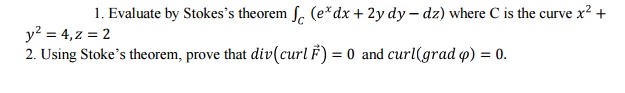
Related Topics