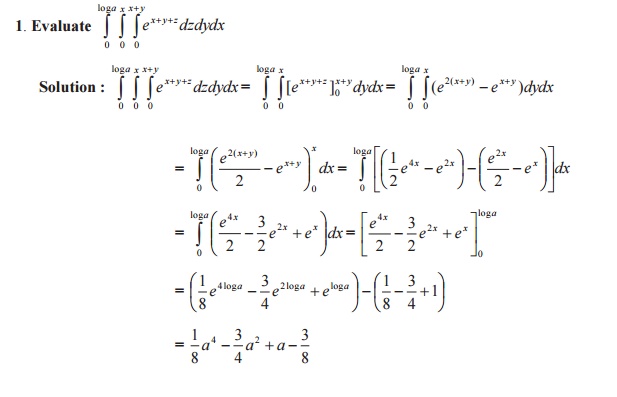Chapter: Mathematics : Multiple Integrals
Multiple Integrals
MULTIPLE
INTEGRALS
Introduction
Evaluation
Of Double Intgrals
Problems
Based On Double Integration In Cartesian Coordinates
Double
Integration In Polar Coordinates
Change
The Order Of Integration
Problems
Based On Area As A Double Integral
Evaluation Of Triple Integrals
INTRODUCTION:
When a unction f(x) is integrated with respect to x between the limits a and b,
get the definite integral
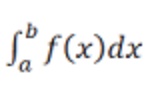
If the integrand is a function f(x,y)
and if it is integrated with respect to x and y repeatedly between the limits x0
and x1 (or x) between the limits y0 and y1 (or
y).
we get a double integral that is denoted
by the symbol
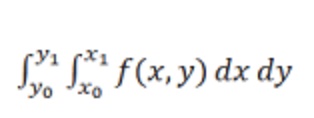
Extending the concept of double integral
one step further, we get the tripe integral
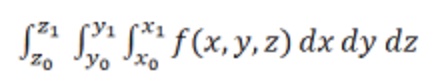
EVALUATION
OF DOUBLE INTGRALS
Before starting on double integrals let’s
do a quick review of the definition of a definite integrals for functions of
single variables. First, when working with the
We think of x's as comimg from the
interval a<x<b. For these integrals we can say that we are integrating
over the interval a<x<b. Note that this does assume that a<b, however,
if we have b<a then we can just use interval b<x<a.
Now, when we derived the definition of
the definite integral we first thought of this as an area problem. We first
asked what the area under the curve was and to do this we broke up the interval
a<x<b into n subintervals of width Del(x) ∆x and choose a point, x1 from
each as shown below.
Each of the rectangles has height of f(x1)
and we could then use the area of each of these rectangles to approximate the
area as follows.
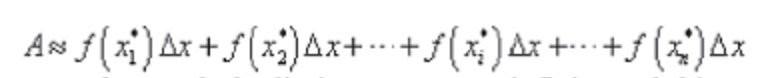
To get the exact area we then took the
limit as n goes to iniinity and this was also the definition of the definite
integral.
we first integrate f(x,y) with respect
to x partially, treating y as a constant temporarily, between x0 and x1. The
resulting function got after the inner integration and substitution of limits
will be a function of y. Then we integrate this function of y with respect to y
between the limits y0 and y1 as usual.
PROBLEMS
BASED ON DOUBLE INTEGRATION IN CARTESIAN COORDINATES
DOUBLE
INTEGRATION IN POLAR COORDINATES:
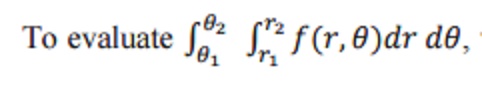, we first integrate w.r.to
r between the limits r1 and r2. Keeping θ1 is fixed and the
resulting expression is integrated w.r.to θ from θ1 to θ2.
In this integral this r1 and
r2 are functions of θ and θ1, θ2 are
constants.
CHANGE
THE ORDER OF INTEGRATION:
The double integral
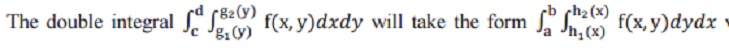
when the order of integration is changed. This
process of converting a given double integral into its equivalent double
integral by changing the order of integration is often called change of order
of integration. To effect the change of order of integration, the region of
integration is identified first, a rough sketch of the region is drawn and then
the new limits are fixed.
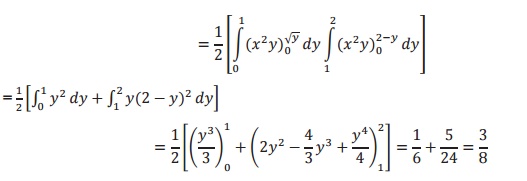
PROBLEMS
BASED ON AREA AS A DOUBLE INTEGRAL:
Area of the region R in Cartesian form
is given by
Area of the region R in polar form is
given by
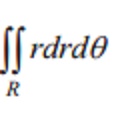
5. Find the area inside the circle
r=asinθ but lying outside the cardiod r=a(1-cosθ)
Solution: Given curves are r=asinθ and r
=a(1-cosθ)
The curves intersect where a sin θ = a
(1-cosθ)
EVALUATION
OF TRIPLE INTEGRALS
To evalute
,
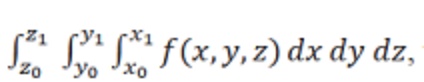we first integrate f(x,y,z) with respect
to x, treating y and x as constants temporarily. The limits x0 and x1
may be constants or unctions of y and z. Then we perform the middle integration
with respect to y, treating function got after
the middle integrtion may be a unction o z only. Finally we perform
the outermost the outermost integration
with respect to z between the constant limits z0 and z1.
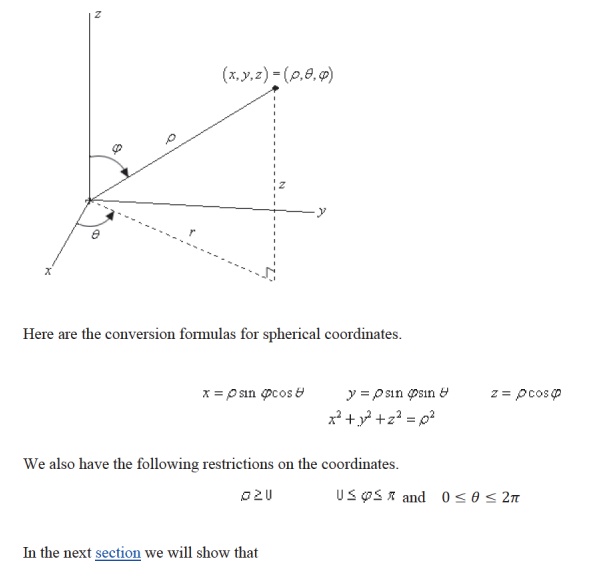
The following sketch shows the relationship
between the Cartesian and spherical coordinate systems.
