Chapter: Mathematics : Functions of several Variables
Functions of several Variables
Functions of several Variables
· Problems based on Partial Derivatives
· Problems based on Euler`s Theorem
· Problems based on Total Derivatives-Differentiation of Implicit Function
· Problems based on Jacobian
· Problems based on Taylor`s and Laurent Series
· Problems based on Maxima and Minima for Functions of Two Variables
· Problems based on Lagrangian Multiplier
Partial Derivatives
Partial Derivatives: Let z=f(x,y) be a function of two Variables x and y, If we keep y as a constant and Vary x alone , then z is a function of x only ,
The derivative of z w.r.to x, treating y as a constant is called the partial derivatives w.r.to x and it is denoted by the symbols
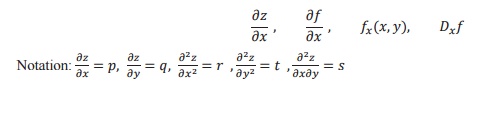
Successive Partial Differentiation:


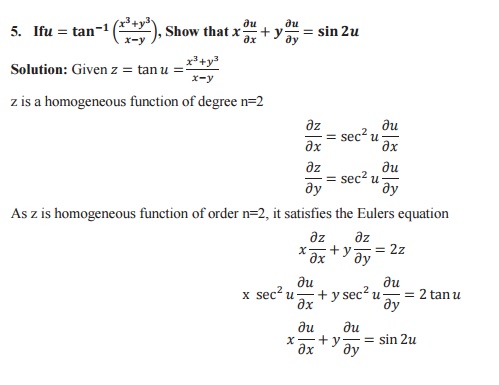
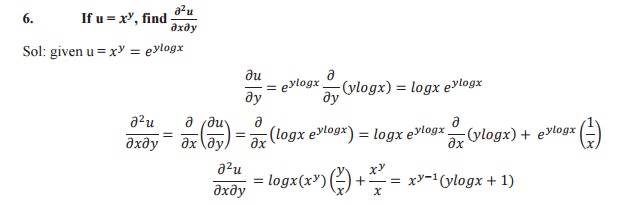
Euler`s Theorem for Homogeneous Function
Euler`s Theorem: If u be a homogeneous function of degree n an x and y then

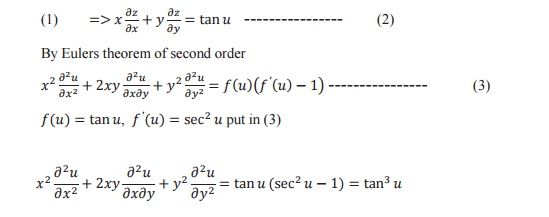

Total Derivatives-Differentiation of Implicit Function
Total Derivative:











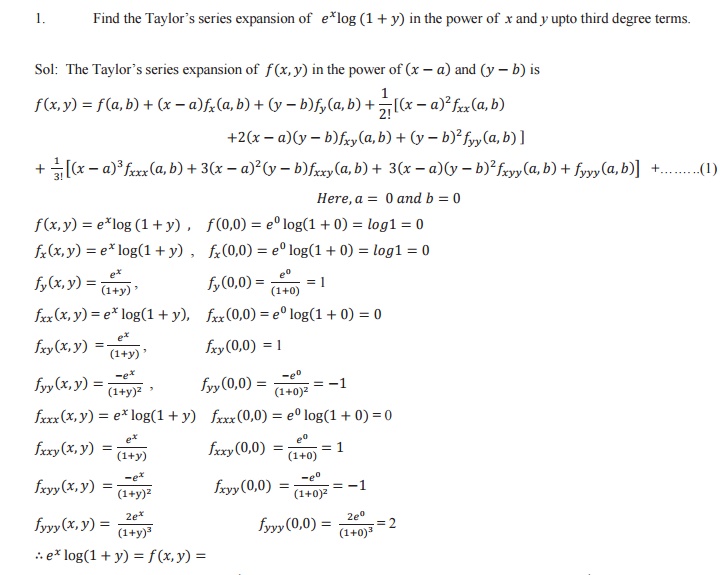
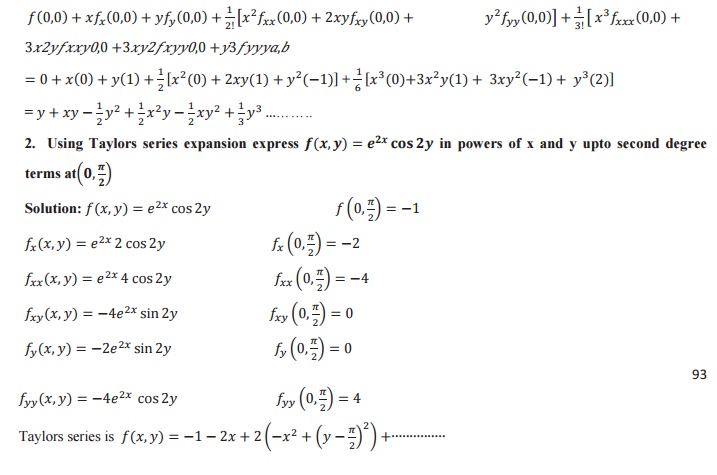

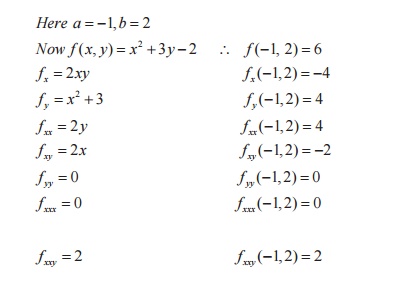

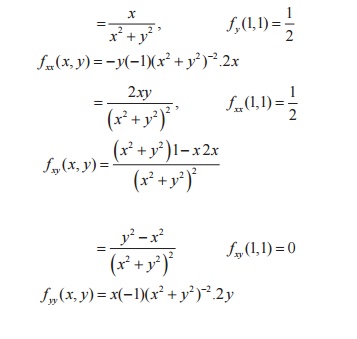
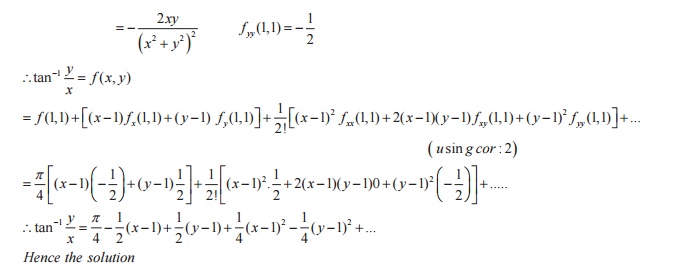
Maxima and Minima and Lagrangian Multiplier
Defn: Maximum Value
if f(a,b) is a maximum value of (x,y) if their exists some neighbourhood of the point (a,b) such that for every point (a+h,b+k) of the neighbourhood
f(a,b)>f(a+h,b+k)
Defn: Minimum Value
if f(a,b) is a maximum value of (x,y) if their exists some neighbourhood of the point (a,b) such that for every point (a+h,b+k) of the neighbourhood
f(a,b)<f(a+h,b+k)
Defn: Extremum Value
if f(a,b) is said to be an extremum value o if f(a,b) it is maximum or minimum
Defn: Lagrangian Multiplier
Suppose we require to find the maximum and minimum values of (x,y,z) where x,y,z are subject to a constraint equation g(x,y,z)=0
We define a function F(x,y,z) = f(x,y,z) + λg(x,y,z) where λ is called Lagrangian Multiplier which is independent of x,y,z.
Problems:



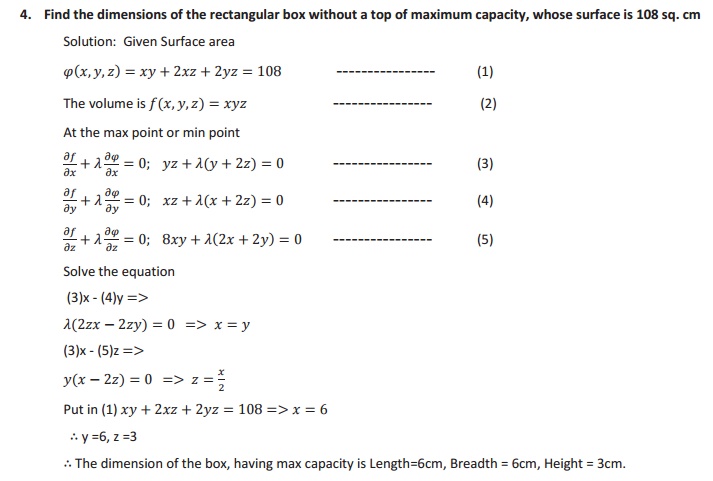





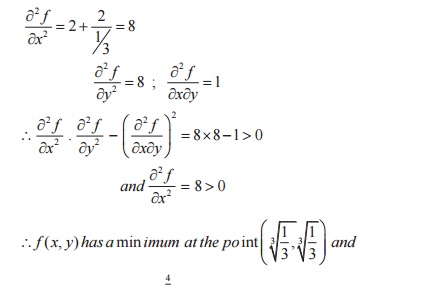






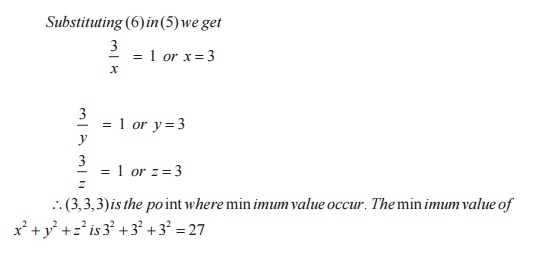

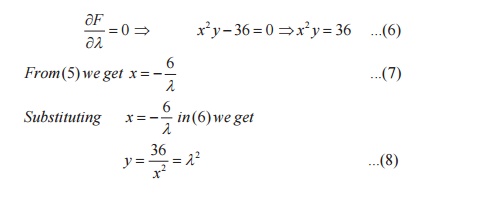


Related Topics