Chapter: Mathematics : Differential Calculus
Differential Calculus
DIFFERENTIAL
CALCULUS
Curvature:
The rate of bending of a curve in any interval is called the curvature of the
curve in that interval.
Curvature
of a circle: The curvature of a circle at any point
on it equals the reciprocal of its radius.
Radius
of curvature: The radius of curvature of a curve at
any point on it is defined as the reciprocal of the curvature

Centre
of curvature: The circle which touches the curve at P
and whose radius is equal to the radius of curvature and its centre is known as
centre of curvature.
Equation of circle of curvature:
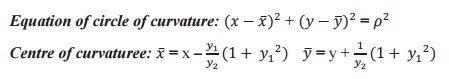
Evolute:
The locus of the centre of curvature is called an evolute
Involute:
If a curve C1 is the evolute of C2 , then C2 is said to be an involute of a curve
C1.
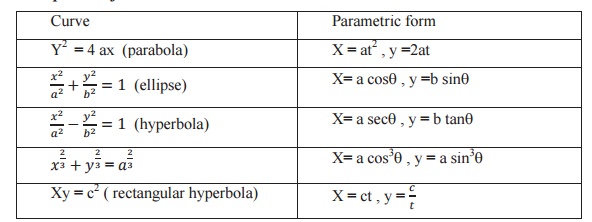
Parametric
equation of some standard curves
Envelope:
A
curve which touches each member of a family of curves is called envelope of
that family curves.
Envelope
of a family of curves: The locus of the ultimate points of
intersection of consecutive members of a family of curve is called the envelope
of the family of curves.
Properties
of envelope and evolute
Property:1:
The normal at any point of a curve is a tangent to its evolute touching at the
corresponding centre of curvature.
Property:2
The difference between the radii of curvature at two points of a curve is equal
to the length of the arc of the evolute between the two corresponding points.
Property:3:
There is one evolute ,but an infinite number of involutes
Property:4
The envelope of a family of curves touches at each of its point. The
corresponding member of that family
Evolute
as the envelope of normals: The normals to a curve form a
family of straight lines.we know that the envelope of the family of these normals
is the locus of the ultimate points of intersection of consecutive normals. But
the centre of curvature of a curve is also the point of consecutive normals.
Hence the envelope of the normals and the locus of the centres of curvature are
the same that is ,the evolute of a curve is the envelope of the normals of the
curve.



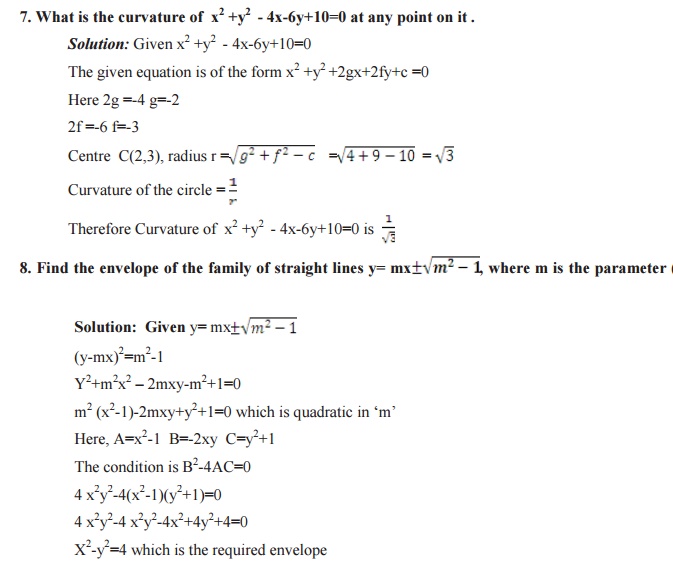




























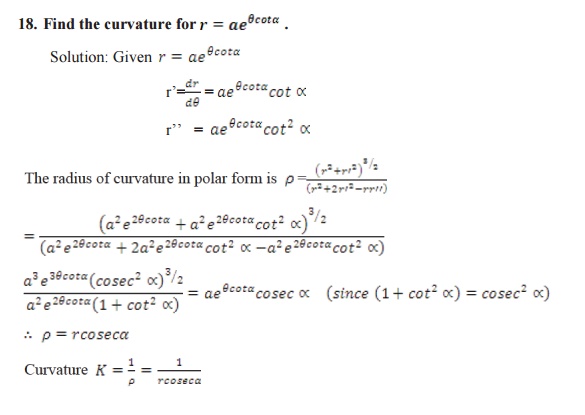









Related Topics