Ordinary Differential Equations

ORDINARY DIFFERENTIAL EQUATIONS

1. Higher Order Linear Differential Equations With Constant Coefficients

2. Method of Variation of Parameters

3. Differential Equations for the Variable Coefficients

4. Simultaneous First Order Linear Equations with Constant Coefficients

ORDINARY DIFFERENTIAL EQUATIONS

1 Introduction:

The study of a differential equation in applied mathematics consists of three phases.

(i) Formation of differential equation from the given physical situation, called modeling.

(ii) Solutions of this differential equation, evaluating the arbitrary constants from the given conditions, and

(iii)Physical interpretation of the solution.

1.1. Higher Order Linear Differential Equations with Constant Coefficients

General form of a linear ifferential equation of the nth order with constant coefficients is

1.2.Note

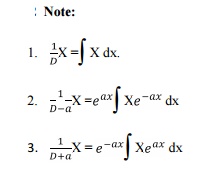
1.3.Solution of the linear differential equation 

Working rule:

i. The general form of the linear differential equation of second order  is

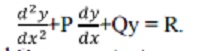
where P and Q are constants and R is a function of x or constant.

ii. Differential operators

The symbol D stands for the operation of differential

1.4. Problems Based On R.H.S Of The Given Differential Equation Is Zero.

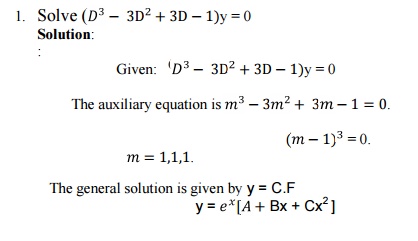
The general solution is given by y = C.F

1.5 Problems Based On P.I.

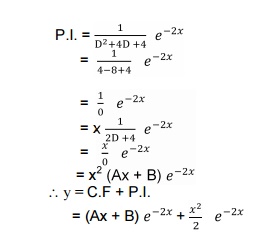
1.6 Problems Based On P.I. =

1.7 Problems Based On R.H.S =

1.8 Problems Based On R.H.S

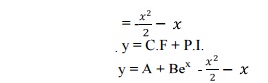
1.9 Problems Based On R.H.S

1.10 Problems Based On

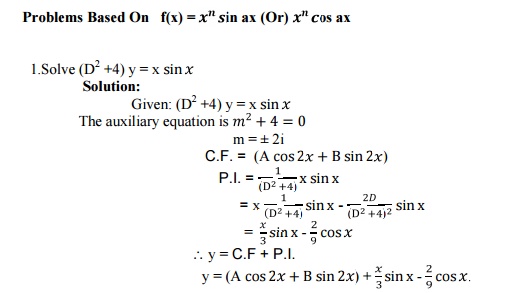
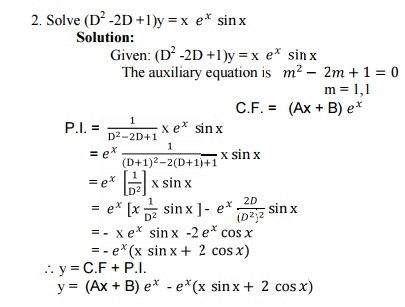
1.11 Problems Based On

1.12 General ODE Problems

1.13 Problems Based On R.H.S

2. Method of Variation of Parameters

This method is very useful in finding the general solution of the second order equation.

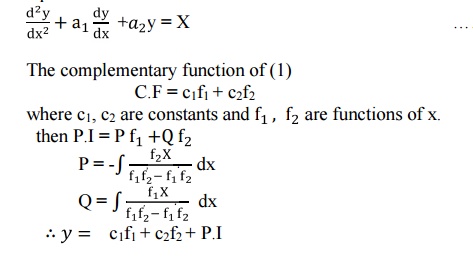
2.1 Problems Based On Method Of Variation Of Parameters

2. Solve (D2 +1) y = cosec x cot x by the method of variation of parameters.

Solution:

Given: (D2 +1) y = cosec x

The auxiliary equation is (m2 +1) = 0       

      m ±i      

2.2. Tutorial Problems

2.3. Differential Equations For The Variable Coefficients  (Cauchy’s Homogeneous Linear Equation)

An equation of the form

3.1 Problems Based On Cauchy' Type 

3.2 Problems Based On Legendre’s Linear Differential Equation

(Equation Reducible To Linear Form )

An equation of the form

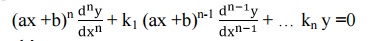
Where k’s are constants and Q is a function of x is called Legendre’s linear differential equations.

Such equations can be reduced to linear equations with constant coefficients by putting

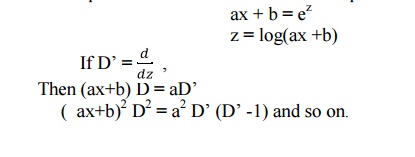
1.Transform the equation

into a differential equation with constant coefficients.

Solution :

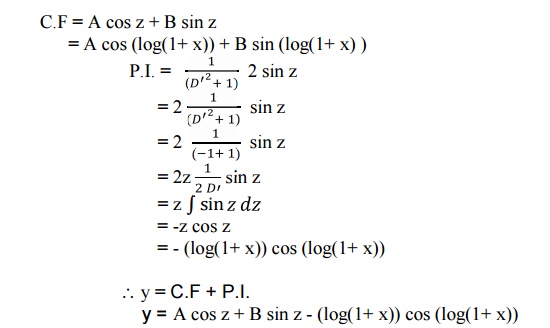
=       -z cos z

=       - (log(1+ x)) cos (log(1+ x))

y= C.F + P.I.

                   y = A cos z + B sin z - (log(1+ x)) cos (log(1+ x))         

3.3.  Tutorial Problems

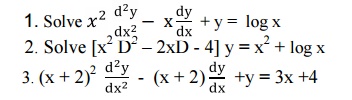
4 Simultaneous First Order Linear Equations With Constant Coefficients

4.1 Simultaneous linear equations

Linear differential equations in which there are two (or) more dependent variables and a single independen Variable. such equations are known as Simultaneous linear equations. Consider the Simultaneous

Equation in two dependent variables x and y and one independent variable.

f1(D) x + g1(D) y = h1(t) … (1)

f2(D) x + g2(D) y = h2(t) … (2)

where f1 ,f2,g1,g2 are polynomials in the operator D.

The number of independent arbitrary constants appearing in the general solution of the system of

Differential equation (1) & (2) is equal to the degree of D in the coefficient determinant       

4.2 Problems Based Simultaneous First Order Linear Equations With Constant Coefficients

4.3.  Tutorial Problems

1. Solve Dx + y = sin 2t ; -x +Dy = cos 2t

2. Solve the simultaneous equations