Chapter: Mathematics (maths) : Laplace Transformation
Laplace Transformation
LAPLACE TRANSFORMATION
1. Laplace transformation-Conditions and existence
2. Transforms of Elementary functions-Basic Properties
3. (a) Transforms of derivatives
(b)Derivatives and integrals of Transforms
(c)Integrals of Transforms
4. Transforms of the unit step functions and impulse function
5. Transforms of periodic functions
6. Inverse Laplace Transform
7. Convolution theorem
8. Initial and final value theorems
9. Solution of linear ODE of Second Order with constant coefficients
LAPLACE TRANSFORM
Introduction
Laplace Transformation named after a Great French mathematician PIERRE SIMON DE LAPLACE (1749-1827) who used such transformations in his researches related to “Theory of Probability”.
The powerful practical Laplace transformation techniques were developed over a century later by the English electrical Engineer OLIVER HEAVISIDE (1850-1925) and were often called “Heaviside -Calculus”.
1 Laplace Transform
Definitions
1. Transformation
A “Transformation” is an operation which converts a mathematical expression to a different but equivalent form
2. Laplace Transformation
Let a function f(t) be continuous and defined for positive values of ‘t’. The Laplace transformation of f(t) associates a function s defined by the equation
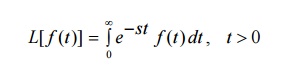
Here, F(s) is said to be the Laplace transform of f(t) and it is written as L[f(t)] or L[f]. Thus F(s) = L(f(t))
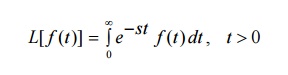
3. Exponential Order
A function f(t) is said to be of exponential order if
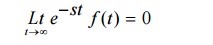
1.1Laplace Transform – Sufficient Conditions For Existence
i) f(t) should be continuous or piecewise continuous in the given closed interval [a, b] where a > 0.
ii) f(t) should be of exponential order.
Example:
1. L[tan t] does not exist since tan t is not piecewise continuous. i.e., tan t has infinite number of infinite
1.2 Problems Based On Laplace Transform – Sufficient Conditions For Existence
1. Show that t2 is of exponential order.
Solution:
Given f(t) = t2
By the definition of exponential order,

![]() Hence t2 is of exponential order.
Hence t2 is of exponential order.
2. Show that the function the following function is not of exponential order f (t ) =et2
Solution:
Given f(t) = et 2
By the definition of exponential order,
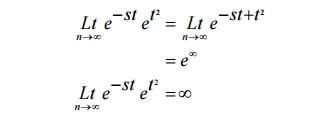
1.3 Define function of class A
A function which is sectionally continuous over any finite interval and is of exponential order is known as a function of class A
2 Transforms Of Elementary Functions- Basic Properties
Important Results
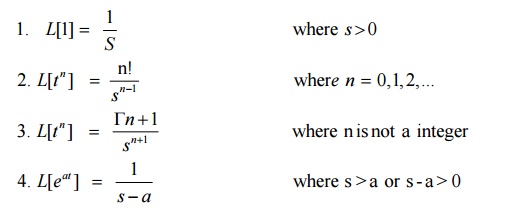
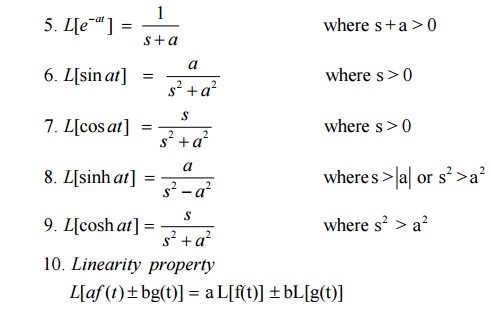
2.1 Problems Based On Transforms Of Elementary Functions- Basic Properties
1. Find L[t5 + e3t + 5e-2t]
Solution:
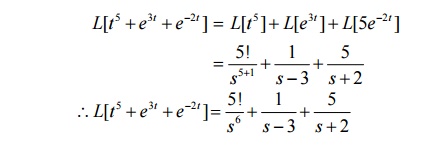
2. Find L[sin 2t+ cos πt – 8cosh 7t +sinh bt]
Solution:

2.2 First Shifting Theorem
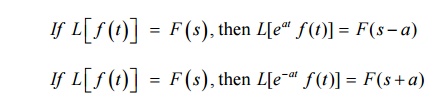
2.3 Second Shifting Theorem
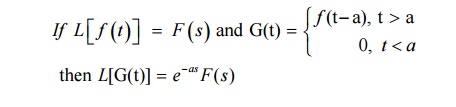
2.4 Problems Based On First And Second Shifting Theorem
1. Find L[tn e-at]
Solution:

2. Find L[eat sinh bt]
Solution
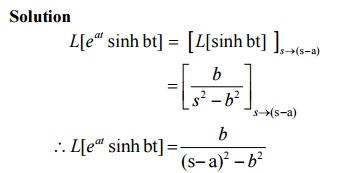
2.5 Tutorial Problems:
1. Find L[cos 4t sin 2t]
2. Find L[sinh22t]
3. Find L[cos(3t-4)
4. Find L[e-tt9]
3 Transforms Of Derivatives And Integrals Of Functions
Properties:
L[ f '( t )] =s L[ f ( t )] -f (0)
L[ f ''(t )] =s2 L[ f (t )] -s f (0) -f'(0)
3.1 Transform of integrals
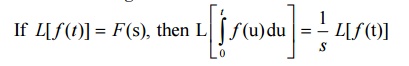
3.2 Derivatives of transform
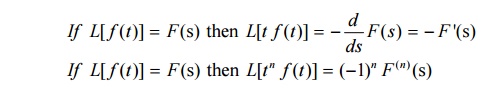
3.3 Problems Based On Derivatives Of Transform
1. Find L[t sin at]
Solution:
We know that

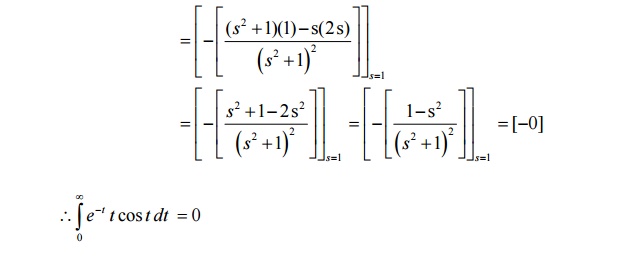

3.4 Tutorial Problems:
1. Find L[t sin2t]
2. Find L[t cos at]
3. Find L[t sin3t cos2t]
3.5 Problems Based On Integrals Of Transform
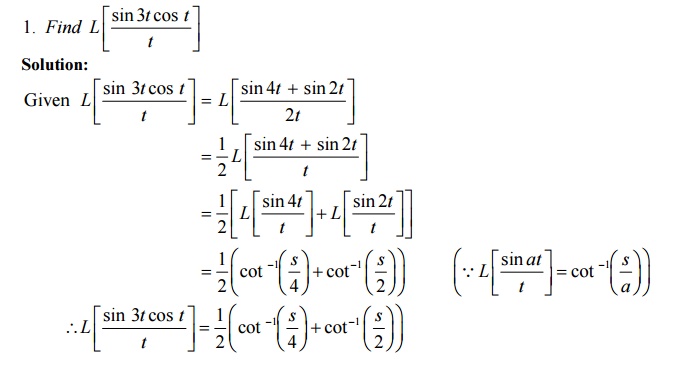
3.6 Tutorial Problems:
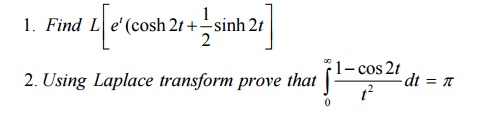
4 Transforms Of Unit Step Function And Impulse Function
4.1 Problems Based On Unit Step Function (Or) Heaviside’s Unit Step Function
1. Define the unit step function.
Solution:
The unit step function, also called Heaviside’s unit function is defined as
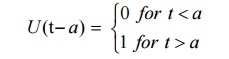
This is the unit step functions at t = a. It can be also denoted by H(t-a).
2. Give the L.T of the unit step function.
Solution:
The L.T. of the unit step function is given by
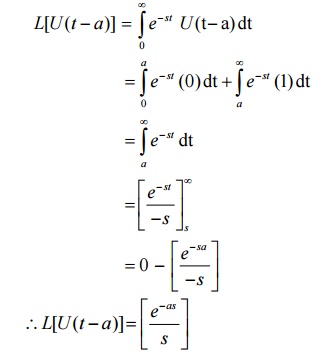
4.2 Tutorial Problems:
1. Give the L.T. of the Dirac Delta function
2. Find the L.T. of t U(t-9).
3. Find L-1[1]
5 Transform Of Periodic Functions
Definition: (Periodic)
A function f(x) is said to be “periodic” if and only if f(x+p) = f(x) is true for some value of p and every value of x. The smallest positive value of p for which this equation is true for every value of x will be called the period of the function.
The Laplace Transformation of a periodic function f(t) with period p given by
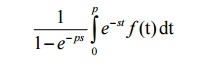
5.1 Problems Based On Transform Of Periodic Functions
1. Find the Laplace Transform of the Half-sine wave rectifier function

5.2 Tutorial Problems:
1. Find the Laplace Transform of triangular wave function
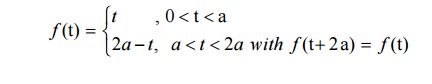
2. Find the Laplace transform of the square wave function (Meoander function) of period ‘a’ defined as

6 Inverse Laplace Transform
a.If L[f(t)] = F(s), then L–1[F(s)] = f(t) where L–1 is called the inverse Laplace transform operator.
b.If F1(s) and F2(s) are L.T. of f(t) and g(t) respectively then
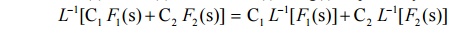
Important Formulas
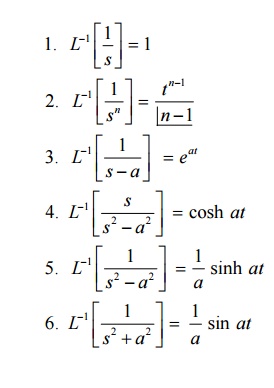
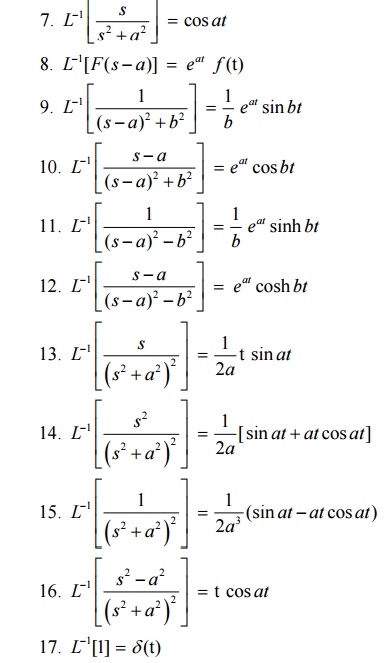
6.1 Problems based on Inverse Laplace Transform
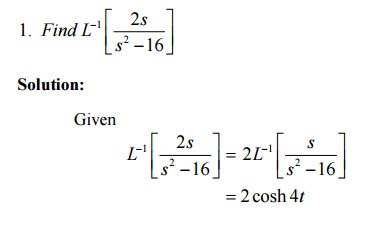

6.2 Inverse Laplace Transforms of derivatives of F(s)
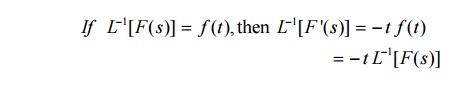
6.3Problems based on Inverse Laplace Transforms of derivatives of F(s)
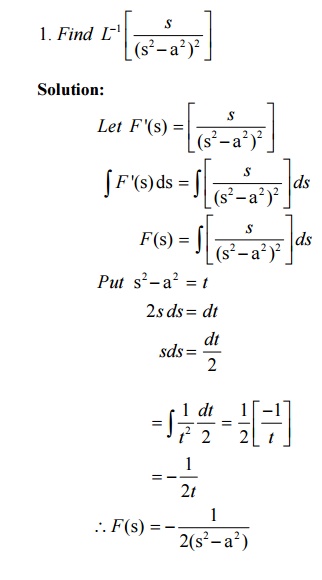
6.4 Inverse Laplace Transform of Integrals

6.5 Problems based on Inverse Laplace Transform of Integrals

6.6 Problems based on Partial fractions method

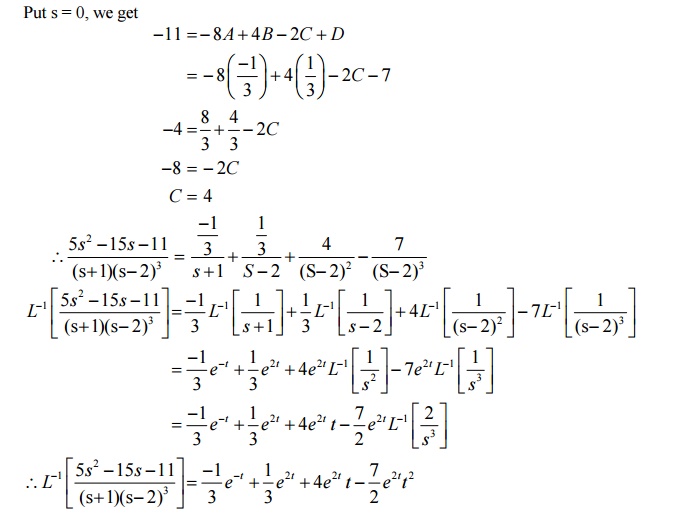
6.7 Second Shifting property

6.8 Problems based on second shifting property

6.9 Tutorial Problems:
a. Find the inverse L.T of Derivatives.

6.10 Change of scale property

6.11 Problems based on Change of scale property
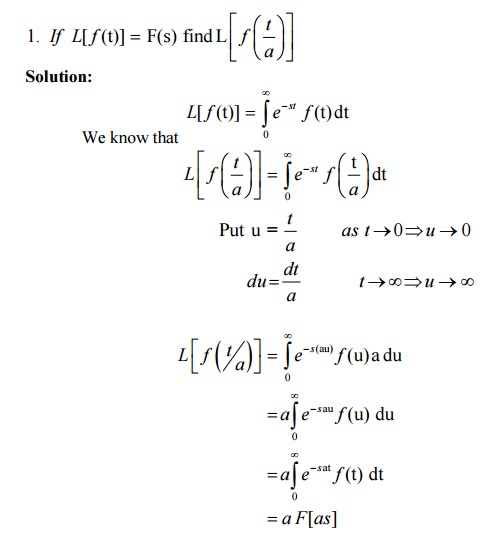
6.12 Tutorial Problems:
1. If L[ f (t)] = F(s) then L[F(t/2) = 2 F(2s)
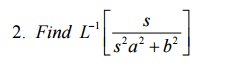
7 Convolution Theorem
If f (t) and g(t) are functions defined for t > = 0,
then L[ f (t ) * g (t )] = L[ f ( t )] L[-g ( t)]
7.1 Problems on Convolution Theorem 1.Define convolution
The convolution of two functions f(t) and g(t) is defined as
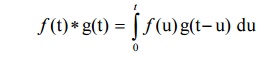
Note: Convolution Integral or Falting integral




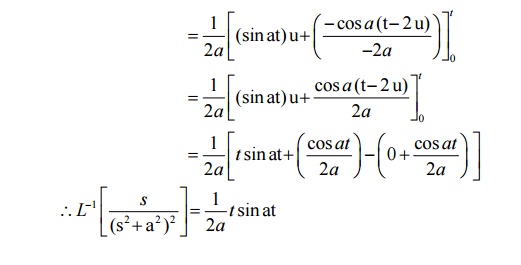
7.2 Tutorial Problems:
Find the inverse Laplace Transform using convolution theorem.
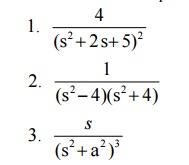
8 Initial and final value theorems
8.1 Initial value theorem
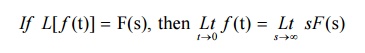
8.2 Final value theorem
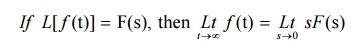
8.3 Problems based on initial value and final value theorems

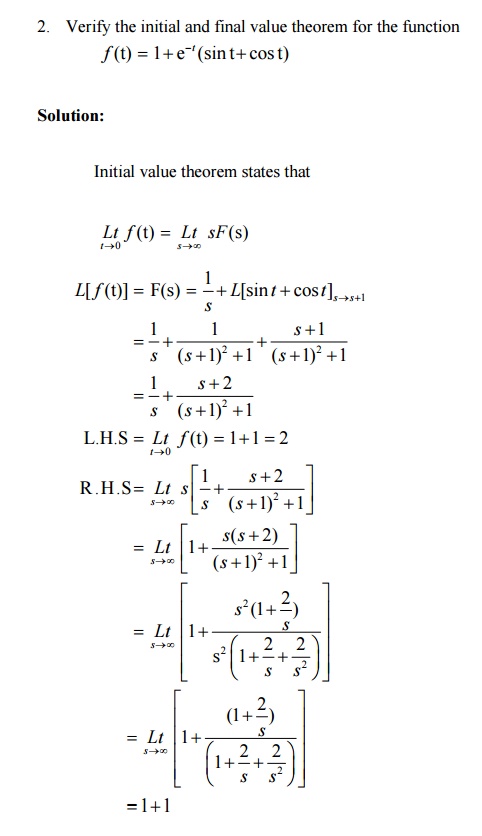

L.H.S = R.H.S
Final value theorem verified.
8.4 Tutorial Problems:
Verify the initial and final value theorems for the functions
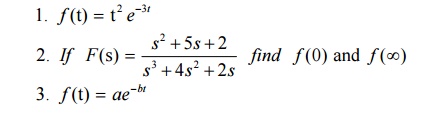
9. Problems based on solution of linear ODE of second order with constant coefficients

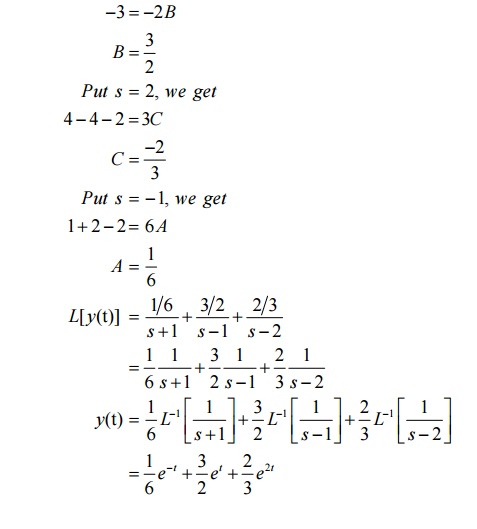
9.2 Tutorial Problems:
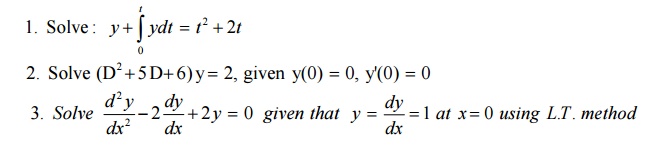
Related Topics