Analytic Functions

ANALYTIC FUNCTIONS

1. Introduction –Function of A Complex Variable

2. Analytic Functions(C-R Equations)

3. Harmonic and Orthogonal Properties Of Analytic Functions

4. Construction of Analytic Functions

5. Conformal Mapping

6. Bilinear Transformation

ANALYTIC FUNCTIONS

1 Introduction: Analytic Functions

1.1 Function of Complex Variable

Many complicated integrals of real functions are solved with the help of complex variable. They are very useful in solving large number of engineering and science problems

1.2 Complex Variable:

1.3  Function of Complex Variable:

z=x+ i y and w=u+ iv are two complex variable. If for each value of z in a given region R of the complex plane there corresponds one or more values of w, then w is called a function of z and it is denoted by w=f(z)=u(x, y)+iv(x, y)where      u(x, y) ,v(x ,y) are real functions of the real variable x and y.

1.4  Single Valued Function

          If for each value of z in R, there is correspondingly only one value of w, the w is called a single valued function of z.

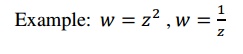
1.5 Multiple  Valued Function

          If for each value of z in R, there is correspondingly more than one value of w, the w is called a multiple valued function of z.

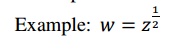
1.6 Neighbourhood of a Point :

          Neighbourhood of a point is a small circular region excluding he points on the boundary with centre at

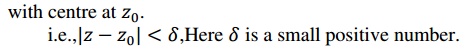
2 Analytic function

2.1 Limit of The Function:

2.2 Continuity:

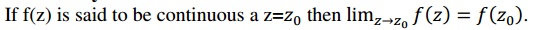
2.3 notes

2.4 Differentiabil ty at the Point

2.5 Note:

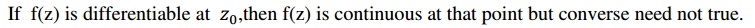
2.6 Analytic (Or) Holomorphic (Or) Regular Function

A function is said to be analytic at a point if its derivative exists not only at the point but also in some neighbourhood of that point.

2.7 Entire Function:

A function which is analytic everywhere in the finite plane is called an entire function.

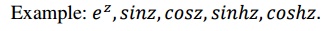
2.8 The Necessary Condition For f(z) To Be Analytic:(Cauchy-Riemann Equations)

i. Cartesian form: The necessary condition for a complex function f(z)=u(x,y)+iv(x,y)

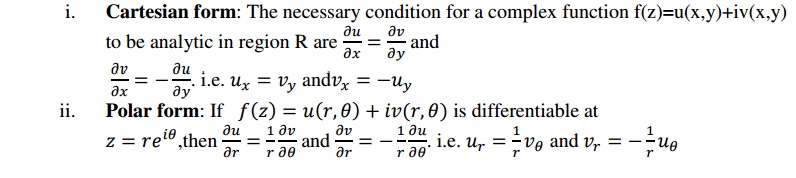
2.9 Problems Based on Analytic Function-Necessary Conditions (C-R Equations)

1.Show that the function f(z)=xy+iy is continuous everywhere but not differentiable anywhere.

Hence f(z) is not differentiable anywhere though it is continuous everywhere

2.   Show that the function f(z)=e^z  is differentiable everywhere in the complex plane.

2.10 Tutorial problems

3 Harmonic and Orthogonal Properties Of Analytic Functions

3.1 Laplace Equation:

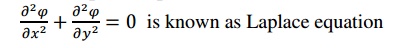
3.2 Properties Of Analytic Functions And Harmonic Conjugate

3.3 Problems Based On Harmonic Conjugate

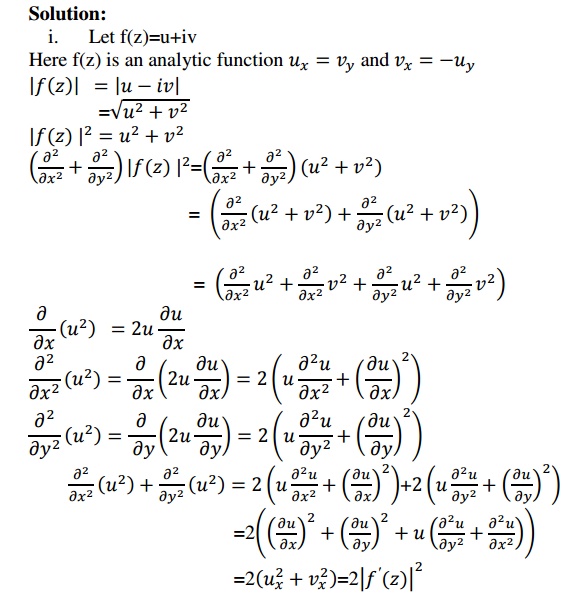
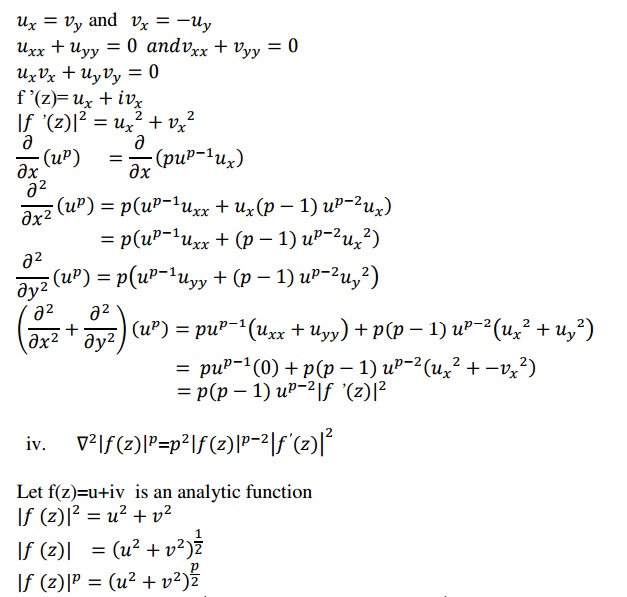
3.3  Problems Based On Harmonic Conjugate

4 Constructions of Analytic Functions (Milne- Thomson Method)

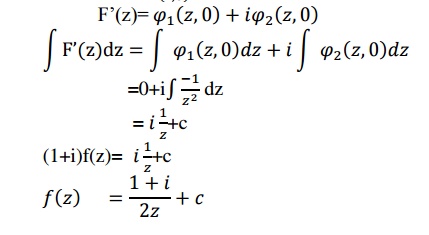
4.5  Tutorial problems

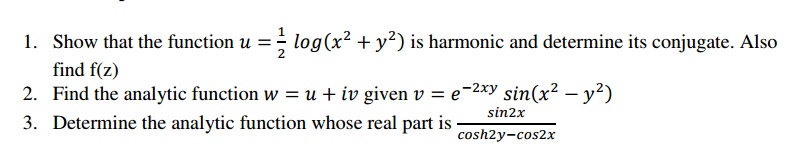
5 Conformal Mapping

5.1 Definition:

The transformation w=f(z) is called as conformal mapping if it preserves angle between every pair of curves through a point, both in magnitude and sense

The transformation w=f(z) is called as Isogonal mapping if it preserves angle between every pair of curves through a point in magnitude but altered in sense

5.2 Standard Transformations

1. Translation:

The transformation  w=C+z  ,where C is a complex constant ,represents a translation

2. Magnification:

The transformation w=Cz ,where C is a real constant ,represents magnification

3. Magnification And Rotation:

The transformation w=Cz,where C is a complex constant ,represents magnification and Rotation

4. Magnification , Rotation And Translation:

The transformation w = Cz + D ,where C,D are complex constant ,represents Magnification, Rotation and Translation

5. Inversion And Reflection:

The transformation w=1/z represents inversion w.r.to the unit circle |z| = 1, followed by reflection in the real axis

5.3 Problems Based on Transformation

1. Find the image of the circle |z| = 1 by the transformation w=z+2+4i

5.4 Tutorial problems

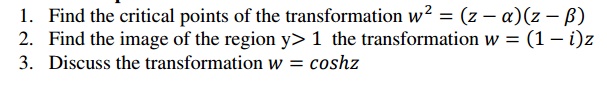
6 Bilinear Transformation

6.1 Definition:

6.2 Note:

x. If one of the point is the point at infinity the quotient of those difference which involve this point is replaced by 1

6.3 Problems based on Bilinear Transformation

6.4  Tutorial problems