Chapter: Mathematics (maths) : Complex Integration
Complex Integration
COMPLEX INTEGRATION
1. Introduction
2. Cauchy’s Theorem
3. Taylor’s and Laurent’s64
4. Singularities
5. Residues
6. Evaluation of real definite Integrals as contour integrals
7. Applications
COMPLEX INTEGRATION
1 Prerequisites
Before starting this topic students should be able to carry out integration of simple real-valued functions and be familiar with the basic ideas of functions of a complex variable. The students should also familiar with line integrals.
2 Introduction
Complex integration is an intuitive extension of real integration. Since a complex number represents a point on a plane while a real number is a number on the real line, the analog of a single real integral in the complex domain is always a path integral. For some special functions and domains, the integration is path independent, but this should not be taken to be the case in general. Given the sensitivity of the path taken for a given integral and its result, parametrization is often the most convenient way to evaluate such integrals.Complex variable techniques have been used in a wide variety of areas of engineering. This has been particularly true in areas such as electromagnetic eld theory, uid dynamics, aerodynamics and elasticity.
3 Cauchy's Theorem
3.1 De nitions
3.1.1Connected Region
A connected region is one which any two points in it can be connected by a curve which lies entirely with in the region.
3.1.2 Simply connected region
A curve which does not cross itself is called a simple closed curve. A region in which every closed curve in it encloses points of the region only is called a simply connected region.
3.1.3 Contour integral
An integral along a simple closed curve is called a contour integral.
3.1.4 Cauchy's Integral Theorem
If a function f(z) is analytic and its derivative f0(z) is continuous at
R
all points inside and on a simple closed curve c, then c f(z)dz = 0:
3.1.5 Cauchy's Integral formula
If f(z) is analytic inside and on a closed curve c of a simply connected region R and if a is any point with in c, then
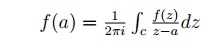
the integration around c being taken in the positive direction.
3.1.6 Cauchy's integral formula for derivative
If a function f(z) is analytic within and on a simple closed curve c and a is any point lying in it, then

3.2 Worked out examples



3.3 Tutorial Problems
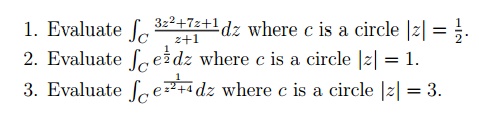
4 Taylor's and Laurent's Series Expansion.
4.1 Taylor's Series.
A function f(z), analytic inside a circle C with center at a, can be expanded in the series
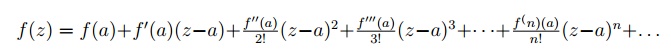
4.2 Laurent's Series.
Let C1; C2 be two concentric circles jz aj = R1 and jz aj = R2 where R2 < R1: Let f(z) be analytic on C1andC2 and in the annular region R between them. Then, for any point z in R,

where the integrals being taken anticlockwise.
4.3 Worked out examples
1. Expand ez in a Taylor's series about z = 0
Solution.

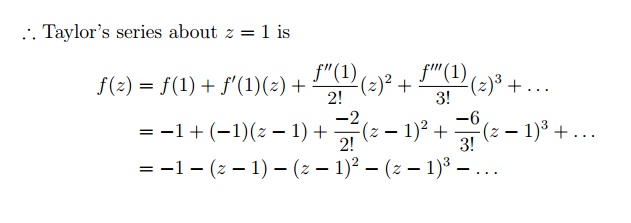

4.4 Tutorial Problems

5 Singularities
5.1 De nitions
5.1.2 Zeros of an analytic function:
If a function f(z) analytic in a region R is zero at a point z = z0 in R then z0 is called a zero of f(z).
5.1.3 Simple Zero:
If f(z0) = 0 and f0(z0) 6= 0 then z = z0 is called a simple zero of f(z) or a zero of the rst order.
5.1.4 Zero of order n:
An analytic function f(z) is said to have a zero of order n if f(z) can be expressed as f(z) = (z z0)m (z) where (z) is analytic and (z0) 6= 0
5.1.5 Singular Points:
A point z = z0 at which a function f(z) fails to be analytic is called a singular point.
5.1.6 Entire function
A function f(z) which is analytic everywhere in the nite plane is called an entire funcction.
5.1.7 Meromorphic function
A function f(z) which is analytic everywhere in the nite plane except at nite number of poles is called a meromorphic function.
5.2 Types of Singularities
5.2.1. Isolated Singularity
A point z = z0 is said to be isolated singularity of f(z) if
1. f(z) is not analytic at z = z0
2. There exist a neighbourhood of z = z0 containing no other singularity.
5.2.2. Removable singularity:
If the principal part of f(z) in Laurent series expansion of f(z) about the point z0 is zero then the point z = z0 is called removable singularity.
5.2.3. Pole:
If we can nd a positive integer n such that limz!a(z a)nf(z) 6= 0 then z = a is called a pole of order n for f(z).
5.2.4. Essential singularity:
If the principal part of f(z) in Laurent series expansion of f(z) about the point z0 contains in nite number of non zero terms then the point z = z0 is called essential singularity.
5.5.3 Worked out Examples

the function f(z) is not de ned at z = 0.
By, L'Hospital rule
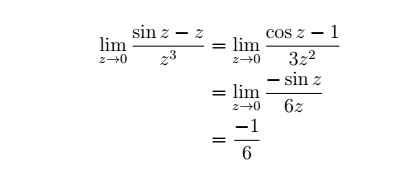
Since the limit exist and is nite, the singularity at z = 0 is a removable singularity.
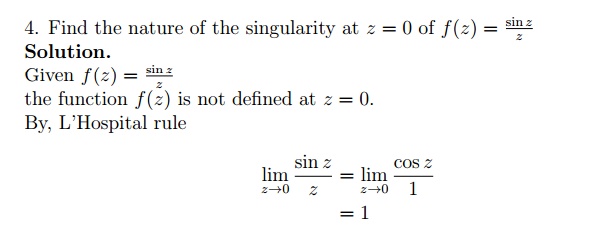
Since the limit exist and is nite, the singularity at z = 0 is a removable singularity.

5.5.4 Tutorial Problems
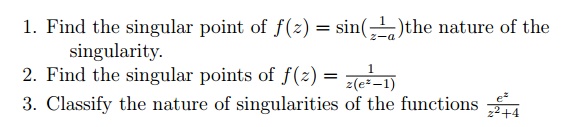
6 Residues
6.1 Definitions:
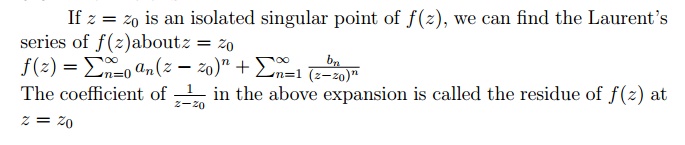
6.1.2 Worked out Examples

6.1.3 Tutorial Problems

6.2 Cauchy Residue Theorem
If f(z) be analytic at all points inside and on a simple closed curve c,
except for a nite number of isolated singularities z1; z2; z3; : : : then
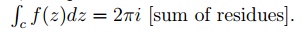
6.2.1Worked out Examples


6.2.2 Tutorial Problems
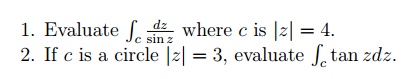
7 Evaluation of real de nite Integrals as contour integrals.
7.1 Contour Integration:
The complex integration along the scro curve used in evaluating the de nite integral is called contour integration. Here we are going to see under three types. They are
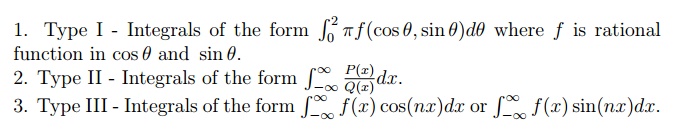
7.2 Type I
7.2.1 Worked out examples
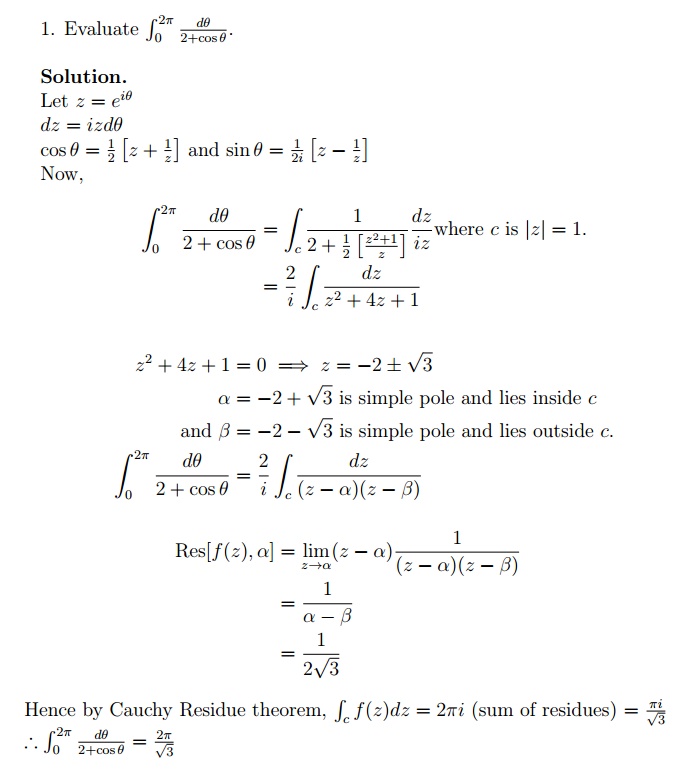

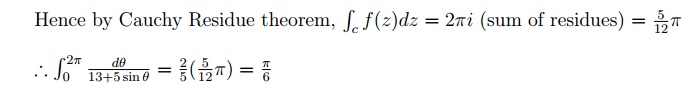
7.2.2 Tutorial Problems
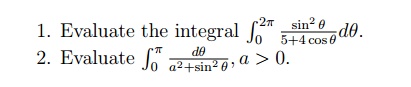
7.3 Type II
7.3.1 Worked out examples

where c consist of the semi circle : jzj = R and the bounding di-ameter [ R; R].
where z = i; 2i are simple poles lie inside and z = I; 2i are simple poles lie outside

the semi-circle becomes very large and the real and imagi-nary parts of any point lying on the semi-circle becomes very large so that

where c is the upper half of the semi circle T with the bounding diam eter [ R; R].
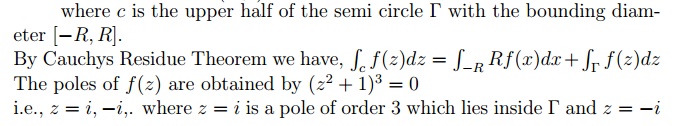
the semi-circle becomes very large and the real and imaginary parts of any point lying on the semi-circle becomes very large so that

7.4.2 Tutorial Problems


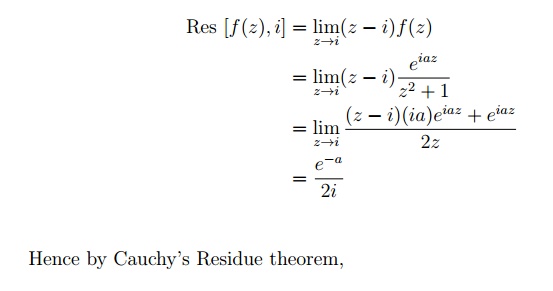




8 Applications:
Blasius Theorem.
The following gure shows a cross-section of a cylinder (not necessarily cir-cular), whose boundary is C,placed in a steady non-viscous ow of an ideal uid; the ow takes place in planes parallel to the xy plane. The cylinder is out of the plane of the paper. The ow of the uid exerts forces and turning moments upon the cylinder. Let X, Y be the components, in the x and y directions respectively, of the force on the cylinder and let M be the anticlockwise moment (on the cylinder) about the origin.
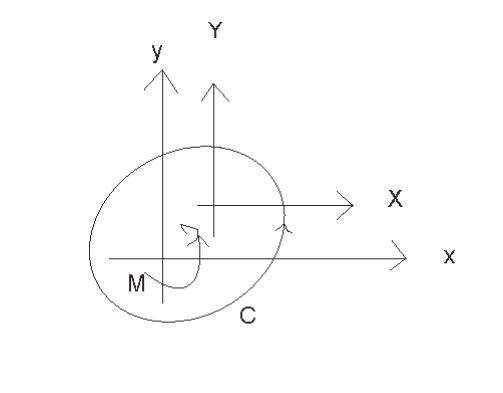

where Re denotes the real part, is the (constant) density of the uid and w = u + iv is the complex potential for the ow both of which are presumed known. We shall nd X; Y and M if the cylinder has a circular cross-section and the boundary is speci ed by jzj = a: Let the ow be a uniform stream with speed U:
Now, using a standard result, the complex potential describing this situation is:
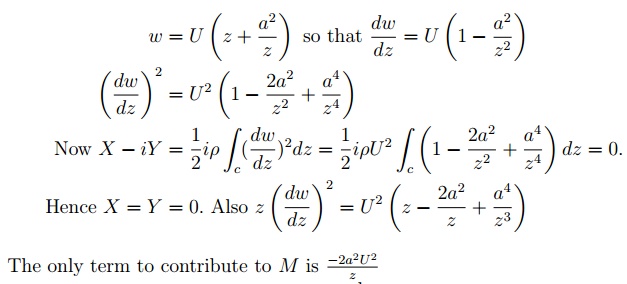
Again using the Key Point above this leads to 4 a2U2i and this has zero real part. Hence M = 0, also. The implication is that no net force or moment acts on the cylinder. This is not so in practice. The discrepancy arises from neglecting the viscosity of the uid.



Related Topics