Chapter: Mathematics (maths) : Two Dimensional Random Variables
Two Dimensional Random Variables
TWO DIMENSIONAL RANDOM VARIABLES
·
Introduction
·
Joint distribution
·
Marginal and Conditional Distribution
·
Covariance
·
Correlation Coefficient
·
Linear Regression
·
Transformation of random variables
Introduction
In the
previous chapter we studied various aspects of the theory of a single R.V. In
this chapter we extend our theory to include two R.V's one for each coordinator
axis X and Y of the XY Plane.
DEFINITION : Let S be the sample space. Let X
= X(S) & Y = Y(S) be two functions each
assigning a real number to each outcome s ∈ S. hen
(X, Y) is a two dimensional random variable.
1 Types of random variables
1. Discrete
R.V.’s
2. Continuous
R.V.’s
Discrete R.V.’s (Two Dimensional Discrete R.V.’s)
If the
possible values of (X, Y) are finite, then (X, Y) is called a two dimensional
discrete R.V. and it can be represented by (xi, y), i = 1,2,….,m.
In the
study of two dimensional discrete R.V.’s we have the following 5 important
terms.
• Joint
Probability Function (JPF) (or) Joint Probability Mass Function.
• Joint
Probability Distribution.
• Marginal
Probability Function of X.
• Marginal
Probability Function of Y.
• Conditional
Probability Function.
1.1 Joint Probability Function of
discrete R.V.’s X and Y
The
function P(X = xi, Y = yj) = P(xi, yj)
is called the joint probability function for discrete random variable X and Y
is denote by pij.
Note
1. P(X = xi,
Y = yj) = P[(X = xi)∩(Y = yj)]
= pij
2. It should
satisfies the following conditions
(i) pij
≥ ∀ i, j (ii) ΣjΣi pij = 1
1.2
Marginal Probability Function of X
If the joint probability
distribution of two random variables X and Y is given then the marginal
probability function of X is given by
Px(xi) = pi (marginal probability function of Y)
Conditional
Probabilities
The conditional probabilities
function of X given Y = yj is given by

SOLVED PROBLEMS ON MARGINAL DISTRIBUTION
Example:2.1.1
From the
following joint distribution of X and Y find the marginal distributions.


3 CONTINUOUS RANDOM VARIABLES
• Two dimensional continuous R.V.’s
If (X, Y)
can take all the values in a region R in the XY plans then (X, Y) is called
two-dimensional continuous random variable.
• Joint
probability density function :



4 REGRESSION
* Line of
regression
The line
of regression of X on Y is given by

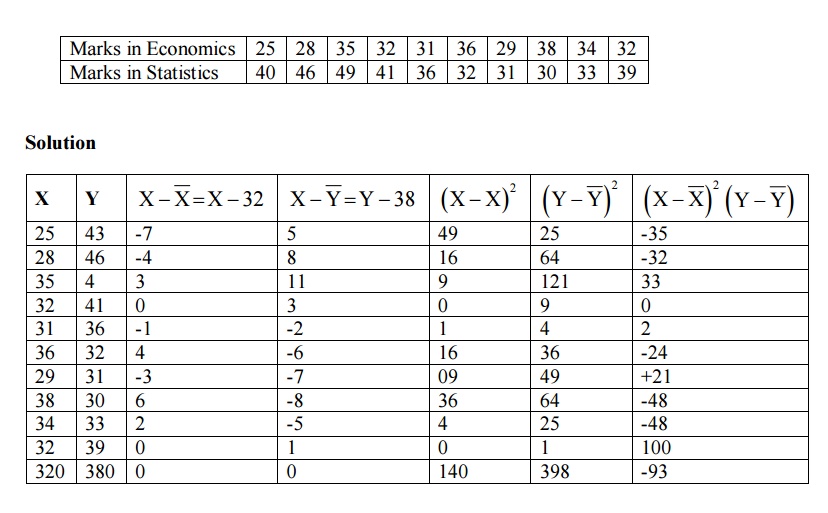
Example:2.4.1
1. From
the following data, find
(i) The two
regression equation
(ii) The
coefficient of correlation between the marks in Economic and Statistics.
(iii) The most
likely marks in statistics when marks in Economic are 30.


5 COVARIANCE
Def : If X and Y are random variables,
then Covariance between X and Y is defined as
Cov (X,
Y) = E(XY) – E(X) . E(Y)
Cov (X,
Y) = 0 [If
X & Y are independent]
6 CORRELATION
Types of
Correlation
• Positive
Correlation
(If two
variables deviate in same direction)
• Negative
Correlation
(If two
variables constantly deviate in opposite direction)
7 KARL-PEARSON’S COEFFICIENT OF CORRELATION
Correlation
coefficient between two random variables X and Y usually denoted by r(X, Y) is
a numerical measure of linear relationship between them and is defined as

SOLVED PROBLEMS ON CORRELATION
Example :2.6.1
Calculated
the correlation coefficient for the following heights of fathers X and their
sons Y

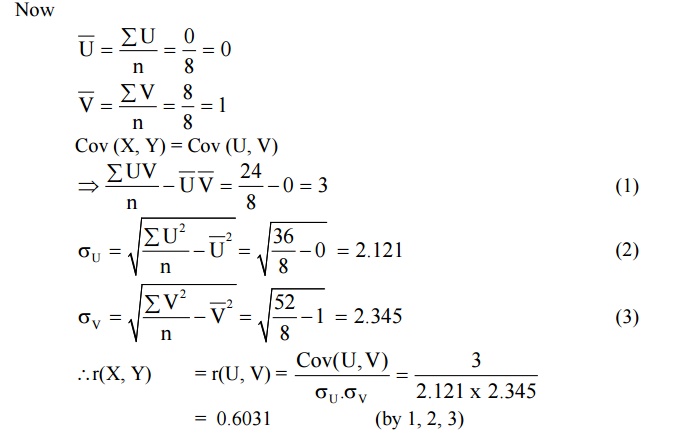

8 TRANSFORMS OF TWO DIMENSIONAL RANDOM VARIABLE
Formula:
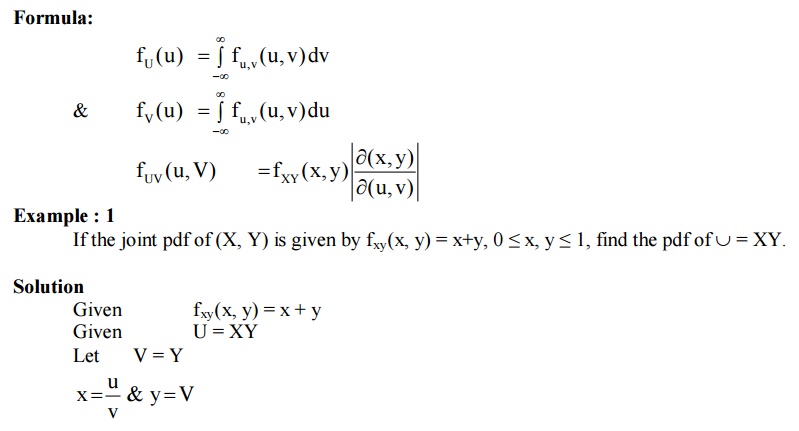
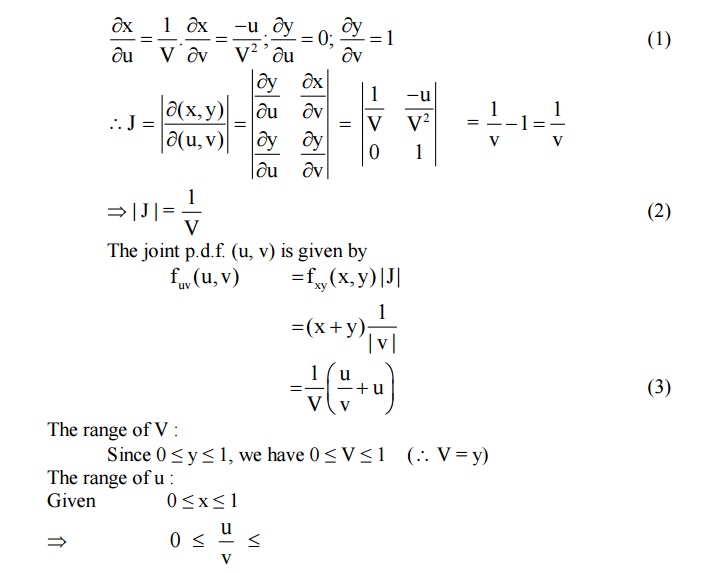
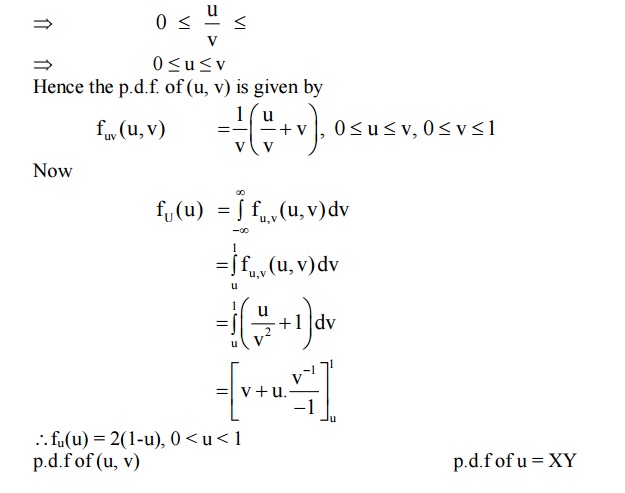

TUTORIAL QUESTIONS
1. The jpdf
of r.v X and Y is given by f(x,y)=3(x+y),0<x<1,0<y<1,x+y<1 and 0
otherwise. Find the marginal pdf of X and Y and ii) Cov(X,Y).
2. Obtain
the correlation coefficient for the following data:
|
X: |
68 |
64 |
75 |
50 |
64 |
80 |
75 |
40 |
55 |
64 |
|
Y: |
62 |
58 |
68 |
45 |
81 |
60 |
48 |
48 |
50 |
70 |
3.The two
lines of regression are 8X-10Y+66=0, 4X-18Y-214=0.The variance of x is 9 find
i) The mean value of x and y. ii) Correlation coefficient between x and y.
4. If X1,X2,…Xn
are Poisson variates with parameter λ=2, use the central limit theorem to find
P(120≤Sn≤160) where Sn=X1+X2+…Xn and n=75.
5. If the
joint probability density function of a two dimensional random variable (X,Y)
is
given by
f(x, y) = x2 + ,
0<x<1,0<y<2= 0, elsewhere Find (i) P(X>1/2)(ii) P(Y<X) and (iii)
![]()
P(Y<1/2/
X<1/2).
6. Two random variables X and Y have
joint density Find Cov (X,Y).
7. If the equations of the two lines
of regression of y on x and x on y are respectively 7x-16y+9=0; 5y-4x-3=0, calculate the coefficient of correlation.
Example
1
The j.d.f of the random
variables X and Y is given
f (x, y) = 8xy, 0 <x <1, 0 y< x
otherwise 0,
Find (i) fX(x) (ii) fY(y)
(iii) f(y/x)
Solution
We know that
(i) The marginal pdf of ‘X’ is
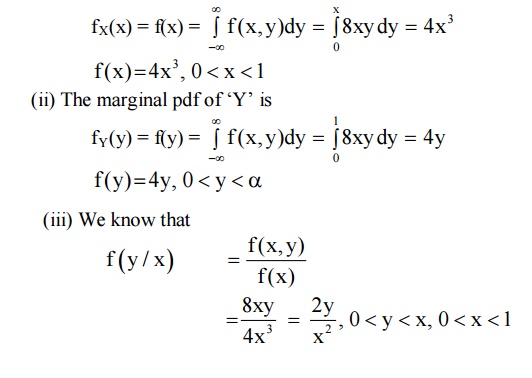

Related Topics