Chapter: Mathematics (maths) : Two Dimensional Random Variables
Important Short Objective Questions and Answers: Two Dimensional Random Variables
Two Dimensional Random Variables
1.Define
Two-dimensional Random variables.
Let S be the sample space associated
with a random experiment E. Let X=X(S) and Y=Y(S) be two functions each
assigning a real number to each s∈S.
Then (X,Y) is called a two dimensional random variable.
2.The following table gives the joint
probability distribution of X and Y. Find the mariginal density functions of X
and Y.
Y /X 1 2 3
1 0.1 0.1 0.2
2 0.2 0.3 0.1

3. If f (x, y)= kxye−(x2 + y2 ) , x ≥ , y0 ≥ 0 is the joint pdf, find k .

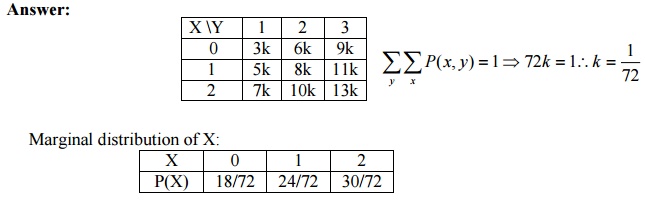
5. The joint p.m.f of (X,Y) is given by P(x,
y) = k(2x + 3y), x = ,1,;02y = ,13,.2.Find the marginal probability
distribution of X.
Answer:
6. If X and Y are independent RVs with
variances 8and 5.find the variance of 3X+4Y. Answer:
Given Var(X)=8 and Var(Y)=5
To find: var(3X-4Y)
We know that Var(aX - bY)=a2Var(X)+b2Var(Y)
var(3X- 4Y)=32Var(X)+42Var(Y) =(9)(8)+(16)(5)=152
7.Find the value of k
if f (x,
y) = k(1−
x)(1−
y)
for0 < x,
y < 1
is to be joint density function.
Answer:
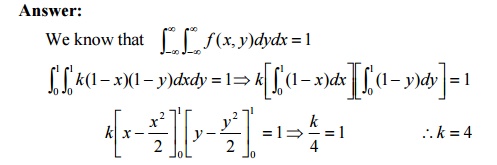
8. If X and Y are random variables
having the joint p.d.f


11. The joint
p.d.f of two random variables X and Y is given by
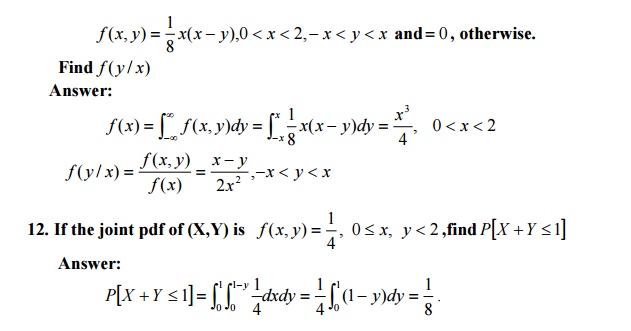
13. If the joint pdf of (X,Y) is f (x, y) = 6e−2x−3y , x ≥ , y0 ≥ ,
find0 the conditional density of Y given
X.
Answer:
Given f (x, y)
= 6e−2x−3y , x ≥ , y0 ≥ ,
0
The Marginal
p.d.f of X:
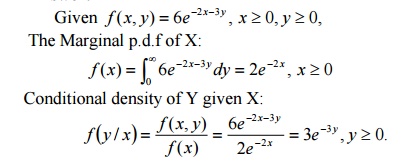
14.Find the probability distribution
of (X+Y) given the bivariate distribution of (X,Y).
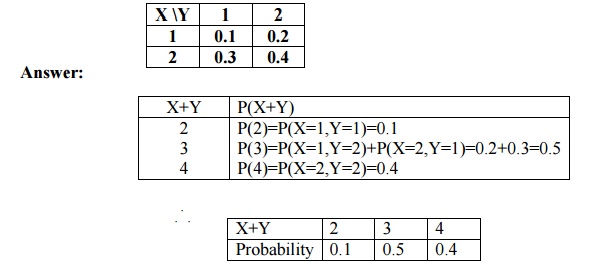
15. The joint p.d.f of (X,Y) is given by
f (x, y)
= 6e−(x+ y) , 0 ≤ x, y ≤ ∞.Are X and Y independent?
Answer:
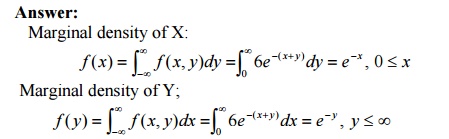
∞ ⇒ f (x)
f (y) = f (x,
y)
X and Y are independent.
16. The joint p.d.f of a bivariate R.V
(X,Y) is given by

17.
Define Co – Variance:
If X and Y are two two r.v.s then co –
variance between them is defined as Cov (X, Y) = E {X – E (X)} {Y – E (Y)}
(ie)
Cov (X, Y) = E (XY) – E(X) E (Y)
18.State
the properties of Co – variance;
1. If
X and Y are two independent variables, then Cov (X,Y) = 0. But the
Converse need not be true
2.Cov (aX, bY) = ab Cov (X,Y)
3.Cov (X + a,Y +b) = Cov (X,Y)
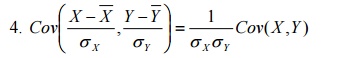
5.Cov(aX+b,cY+d)=acCov(X,Y)
6.Cov
(X+Y,Z) = Cov ( X,Z) + Cov (Y,Z)
7. Cov(aX +
bY,cX + dY) =
acσ X
2 + bdσY
2 + (ad +
bc)Cov(X ,Y) whereσ X 2
=
Cov(X
, X ) = var(X
)andσY
2 =
Cov(Y,Y)
=
var(Y)
19.Show that Cov(aX+b,cY+d)=acCov(X,Y)
Answer:
Take
U= aX+b and V= cY+d
Then E(U)=aE(X)+b and E(V)= cE(Y)+d
U-E(U)= a[X-E(X)] and V-E(V)=c[Y-E(Y)]
Cov(aX+b,cY+d)=
Cov(U,V)=E[{U-E(U)}{V-E(V)}] = E[a{X-E(X)} c{Y-E(Y)}] =ac
E[{X-E(X)}{Y-E(Y)}]=acCov(X,Y)
20.If X&Y are independent R.V’s
,what are the values of Var(X1+X2)and Var(X1-X2)
Answer:
Var(X1 ±
X2 =) Var(X1 +)
Var(X2 )(Since X andY are independent RV then Var(aX ±
bX) = a2Var(X) +
b2Var(X) )
21.If
Y1& Y2 are independent R.V’s ,then covariance (Y1,Y2)=0.Is
the converse of the above statement true?Justify your answer.
Answer:
The converse is not true . Consider
X
- N(0,1)and Y = X2 sin ceX −
N( 1,),0
E(X
) = ; 0E(X
3 ) =
E(XY)
=
0sin
ce all odd moments vanish.
∴cov(XY)
=
E(XY) − E(X )E(Y)
=
E(X 3 ) −
E(X )E(Y) =
0
∴cov(XY)
=
0 but X &Y areindependent
22.Show that cov2
(X ,Y) ≤
var(X
) var(Y)
Answer:
cov(X ,Y) =
E(XY) − E(X )E(Y)
We know that [E(XY)]2
≤
E(X 2 )E(Y 2 )
cov2
(X ,Y) = [E(XY)]2
+
[E(X
)]2
[E(Y)]2
−
2E(XY)E(X )E(Y)
≤ E(X
)2 E(Y)2 +
[E(X
)]2
[E(Y)]2
−
2E(XY)E(X
)E(Y)
≤ E(X
)2 E(Y)2 +
[E(X
)]2
[E(Y)]2
−
E(X
2 )E(Y)2 −
E(Y
2 )E(X )2
= {E(X 2 ) − [E(X )]2 }{E(Y 2 ) − [E(Y)]2 }≤ var(X )
var(Y)
23.If X and Y are independent random
variable find covariance between X+Y and X-Y. Answer:
cov[X
+
Y, X − Y ]=
E[(X
+
Y)(X − Y)]−
[E(X
+
Y)E(X − Y)]
= E[X
2 ] −
E[Y
2 ] −
[E(X
)]2
+
[E(Y)]2
= var(X
) −
var(Y)
24.X
and Y are independent random variables with variances 2 and 3.Find the variance
3X+4Y.
Answer:
Given
var(X) = 2, var(Y) = 3
We
know that var(aX+Y) = a2var(X)
+ var(Y)
And var(aX+bY) = a2var(X) + b2var(Y)
var(3X+4Y)
= 32var(X) + 42var(Y) = 9(2) + 16(3) = 66
25.
Define correlation
The correlation between two RVs X and Y
is defined as
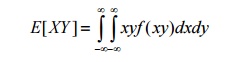
26.
Define uncorrelated
Two RVs are uncorrelated with each
other, if the correlation between X and Y is equal to the product of their means.
i.e.,E[XY]=E[X].E[Y]


33.
State the equations of the two regression lines. what is the angle between
them? Answer:
Regression lines:
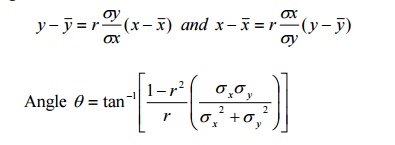
34. The
regression lines between two random variables X and Y is given by 3X
+
Y = 10 and3X +
4Y = 12 .Find the correlation between X
and Y.
Answer:
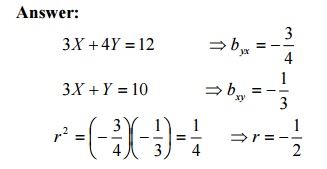
35.Distinguish between correlation and regression.
Answer:
By correlation we mean the casual relationship
between two or more variables. By regression we mean the average relationship between two or more variables.

standard normal distribution as n → ∞ provided
the m.g.f of xi exist.
37.The
lifetime of a certain kind of electric bulb may be considered as a RV with mean
1200 hours and S.D 250 hours. Find the probability that the average life time
of exceeds 1250 hours using central limit theorem.
Solution:
Let X denote the life time of the 60 bulbs.
Then µ = E(X)= 1200 hrs. and Var(X)=(S.D)2=
σ2=(250)2hrs.

38.Joint
probability distribution of (X, Y)
Let (X,Y) be a two dimensional discrete
random variable. Let P(X=xi,Y=yj)=pij. pij
is called the probability function of (X,Y) or joint probability distribution.
If the following conditions are satisfied
1.pij
≥
0 for all i and j
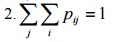
The set of triples (xi,yj,
pij) i=1,2,3……. And j=1,2,3……is called the Joint probability distribution
of (X,Y)
39.Joint
probability density function
If (X,Y) is a two-dimensional continuous RV such
that
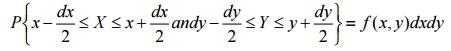
Then
f(x,y) is called the joint pdf of (X,Y) provided the following conditions
satisfied.
f (x, y)
≥
0
for all (x, y)∈(−∞,∞)
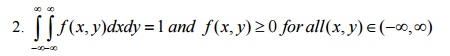
40.Joint
cumulative distribution function (joint cdf)
If (X,Y) is a two dimensional RV then F(x,
y) = P(X ≤
x,Y ≤ y) is called
joint cdf of (X,Y) In the discrete case,
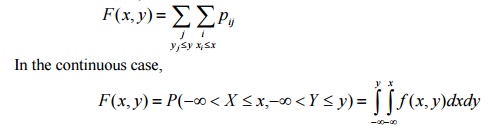
41.Marginal probability
distribution(Discrete case )
Let (X,Y) be a two
dimensional discrete RV and pij=P(X=xi,Y=yj)
then
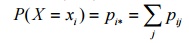
is
called the Marginal probability function.
The collection of pairs
{xi,pi*} is called the Marginal probability distribution
of X.
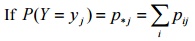
then the collection of pairs {xi,p*j} is called the Marginal probability distribution of Y.
42.Marginal density function (Continuous
case )
Let f(x,y) be the joint
pdf of a continuous two dimensional RV(X,Y).The marginal density
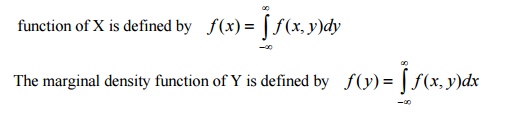
43.Conditional
probability function
If
pij=P(X=xi,Y=yj) is the Joint probability
function of a two dimensional discrete RV(X,Y)
then the conditional probability function X given
Y=yj is defined by
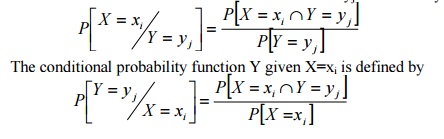
The conditional probability function Y given X=xi
is defined by
44.Conditional
density function
Let f(x,y) be the joint pdf of a continuous two
dimensional RV(X,Y).Then the Conditional
density function of X given Y=y is defined by f (X Y) = fXY (x, y) /fY (y) ,where f(y)=marginal

45.Define statistical properties
Two jointly distributed RVs X and Y are
statistical independent of each other if and only if the joint probability
density function equals the product of the two marginal probability density
function
i.e.,
f(x,y)=f(x).f(y)
46.The joint p.d.f of (X,Y) is given by f
(x,
y) = e−(x+
y) 0 ≤
x,
y ≤ ∞ .Are X and Y are
independent?
Answer:
Marginal densities:
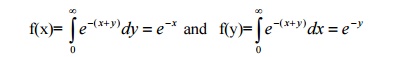
X
and Y are independent since f(x,y)=f(x).f(y)
47.Define Co – Variance :
If X and Y are two two r.v.s then co –
variance between them is defined as Cov (X, Y) = E {X – E (X)} {Y – E (Y)}
(ie) Cov (X, Y) = E (XY) – E(X) E (Y)
48.
State the properties of Co – variance;
1. If
X and Y are two independent variables, then Cov (X,Y) = 0. But the
Converse need not be true
2.Cov (aX, bY) = ab Cov (X,Y)
3.Cov (X + a,Y +b) = Cov (X,Y)
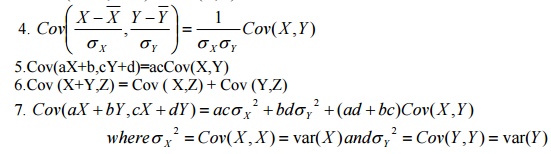
49.Show that Cov(aX+b,cY+d)=acCov(X,Y)
Answer:
Take
U= aX+b and V= cY+d
Then E(U)=aE(X)+b and E(V)= cE(Y)+d
U-E(U)= a[X-E(X)] and V-E(V)=c[Y-E(Y)]
Cov(aX+b,cY+d)= Cov(U,V)=E[{U-E(U)}{V-E(V)}] =
E[a{X-E(X)} c{Y-E(Y)}] =ac E[{X-E(X)}{Y-E(Y)}]=acCov(X,Y)
Related Topics