Chapter: Mathematics (maths) : Random Processes
Random Processes
RANDOM PROCESSES
· Introduction
· Classification
· stationary processes
· Markov processes
· Poisson processes
· Discrete parameter Markov chains
· Chapman Kolmogorov Equation
· Limiting distribution
· Random Telegraph processes
Introduction
In previews pages, we discussed about random variables. Random variable is a function of the possible outcomes of a experiment. But, it does not include the concept of time. In the real situations, we come across so many time varying functions which are random in nature. In electrical and electronics engineering, we studied about signals.
Generally, signals are classified into two types.
(i) Deterministic
(ii) Random
Here both deterministic and random signals are functions of time. Hence it is possible for us to determine the value of a signal at any given time. But this is not possible in the case of a random signal, since uncertainty of some element is always associated with it. The probability model used for characterizing a random signal is called a random process or stochastic process.
RANDOM PROCESS CONCEPT
A random process is a collection (ensemble) of real variable {X(s, t)} that are functions of a real variable t where s ∈ S, S is the sample space and t ∈T. (T is an index set).
REMARK
i) If t is fixed, then {X(s, t)} is a random variable.
ii) If S and t are fixed {X(s, t)} is a number.
iii) If S is fixed, {X(s, t)} is a signal time function.
NOTATION
Here after we denote the random process {X(s, t)} by {X(t)} where the index set T is assumed to be continuous process is denoted by {X(n)} or {Xn}.
A comparison between random variable and random process

Random Variable
A function of the possible outcomes of an experiment is X(s)
Outcome is mapped into a number x.
Random Process
A function of the possible outcomes of an experiment and also time i.e, X(s, t)
Outcomes are mapped into wave from which is a fun of time 't'.
CLASSIFICATION OF RANDOM PROCESSES
We can classify the random process according to the characteristics of time t and the random variable X = X(t) t & x have values in the ranges –∞< t <∞ and –∞< x <∞.
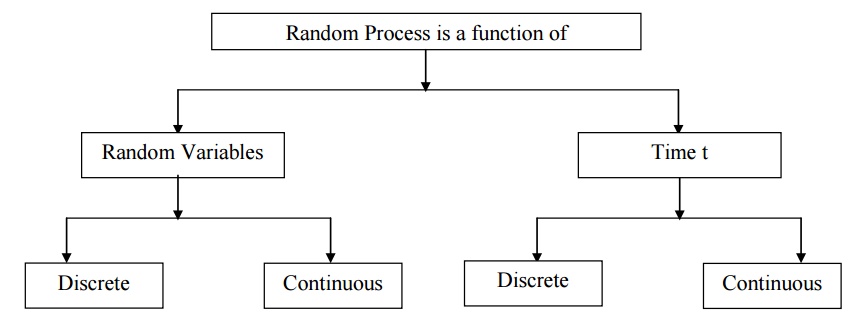
1 CONTINUOUS RANDOM PROCESS
If 'S' is continuous and t takes any value, then X(t) is a continuous random variable.
Example
Let X(t) = Maximum temperature of a particular place in (0, t). Here 'S' is a continuous set and t ≥ 0 (takes all values), {X(t)} is a continuous random process.
2 DISCRETE RANDOM PROCESS
If 'S' assumes only discrete values and t is continuous then we call such random process {X(t) as Discrete Random Process.
Example
Let X(t) be the number of telephone calls received in the interval (0, t). Here, S = {1, 2, 3, …}
T = {t, t ≥ 0}
∴ {X(t)} is a discrete random process.
3 CONTINUOUS RANDOM SEQUENCE
If 'S' is a continuous but time 't' takes only discrete is called discrete random sequence. Example: Let Xn denote the outcome of the nth toss of a fair die.
Here S = {1, 2, 3, 4, 5, 6} T = {1, 2, 3, …}
∴ (Xn, n = 1, 2, 3, …} is a discrete random sequence.
CLASSIFICATION OF RANDOM PROCESSES BASED ON ITS SAMPLE
FUNCTIONS Non-Deterministic Process
A Process is called non-deterministic process if the future values of any sample function cannot be predicted exactly from observed values.
Deterministic Process
A process is called deterministic if future value of any sample function can be predicted from past values.
1 STATIONARY PROCESS
A random process is said to be stationary if its mean, variance, moments etc are constant. Other processes are called non stationary.
1. 1st Order Distribution Function of {X(t)}
For a specific t, X(t) is a random variable as it was observed earlier.
F(x, t) = P{X(t) ≤ x} is called the first order distribution of the process {X(t)}.
1st Order Density Function of {X(t)}

2nd Order distribution function of {X(t)}
F (x 1 , x 2 ; t 1 , t 2 ) = P {X (t 1 ) ≤ x 1 ; X (t 2 ) ≤ x2 }is the point distribution of the random variables X(t1) and X(t2) and is called the second order distribution of the process {X(t)}.
2nd order density function of {X(T)}

2 First - Order Stationary Process
Definition
A random process is called stationary to order, one or first order stationary if its 1st order density function does not change with a shift in time origin.
In other words,
f X (x 1 , t 1 ) = f X (x 1 , t 1 + C)must be true for any t1 and any real number C if {X(t1)} is to be a first order stationary process.
Example :3.3.1
Show that a first order stationary process has a constant mean.
Solution
Let us consider a random process {X(t1)} at two different times t1 and t2.

Mean process {X(t1)} = mean of the random process {X(t2)}.
Definition 2:
If the process is first order stationary, then Mean = E(X(t)] = constant
4 Second Order Stationary Process
A random process is said to be second order stationary, if the second order density function stationary.
f (x 1 , x 2 ; t 1 , t 2 ) = f (x 1 , x 2 ; t 1 + C, t 2 + C )∀x 1 , x2 and C.
E (X12 ), E (X 22 ), E (X1 , X2 )denote change with time, where
X = X(t1); X2 = X(t2).
5 Strongly Stationary Process
A random process is called a strongly stationary process or Strict Sense Stationary
Process (SSS Process) if all its finite dimensional distribution are invariance under translation of time 't'.
fX(x1, x2; t1, t2) = fX(x1, x2; t1+C, t2+C)
fX(x1, x2, x3; t1, t2, t3) = fX(x1, x2, x3; t1+C, t2+C, t3+C) In general
fX(x1, x2..xn; t1, t2…tn) = fX(x1, x2..xn; t1+C, t2+C..tn+C) for any t1 and any real number C.
6 Jointly - Stationary in the Strict Sense
{X(t)} and Y{(t)} are said to be jointly stationary in the strict sense, if the joint distribution of X(t) and Y(t) are invariant under translation of time.
Definition Mean:

7Auto Correlation of a Random Process
Let X(t1) and X(t2) be the two given numbers of the random process {X(t)}. The auto correlation is
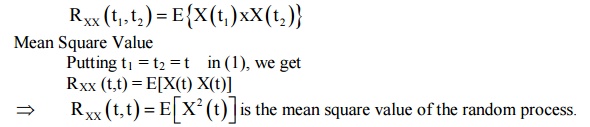
8 Auto Covariance of A Random Process

Where CXX (t1, t2) denotes the auto covariance.
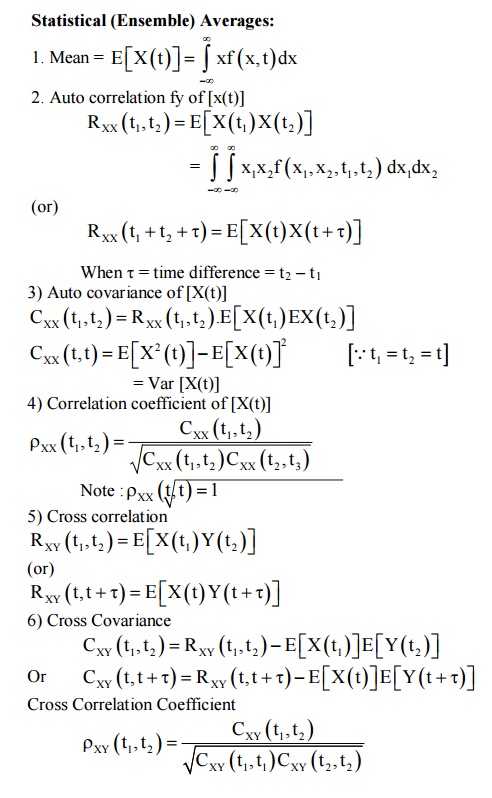
FIRST ORDER STRICTLY STATIONARY PROCESS
Stationary Process (or)
Strictly Stationary Process (or) Strict Sense Stationary Process [SSS Process]
A random process X(t)
is said to be stationary in the strict sense, it its statistical
characteristics do not change with time.
Stationary Process:
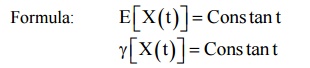
1) Consider the RP X(t)
= Cos (w0t +θ) where θis
uniformly distributed in the interval -π
to π.
Check whether X(t) is stationary or not? Find the first and Second moments of
the process.
Given
X(t) = cos (W0t + θ)
Where θis
uniformly distributed in (-π, π)

To prove (i)
X(t) is SSS process
(ii)
E[X(t)] = Constant
(iii)
Var [X(t)] = Constant
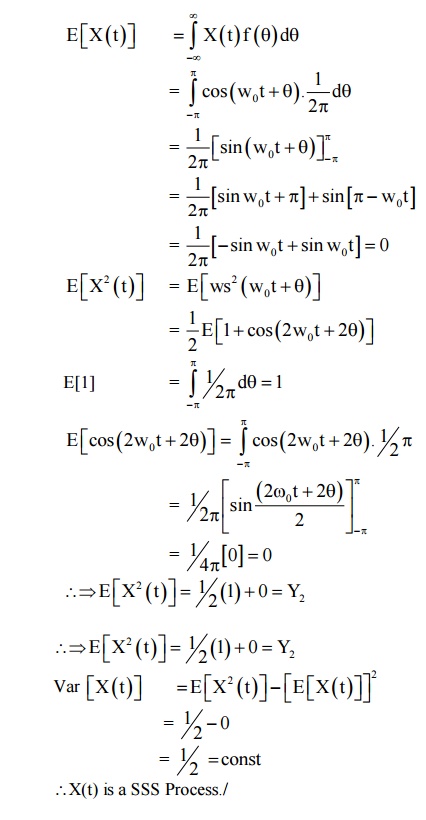
S.T
the RP X(t): Acos (w 0t +θ
is not stationary if A and w0 are constants and θis
uniformly distributed random variable in
(0, π).
In X(t) = Acos (w 0t +θ
In 'θ'uniformly
distributed

∴N(t)
is not a stationary process.
SECOND ORDER AND WIDE SENSE STATIONARY
PROCESS
A Process is said to be second order
stationary, if the second order density function statistics.
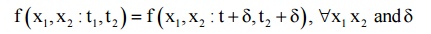
If a random process X(t) is WSS then it must also be
covariance stationary. In X(t) is WSS
i)
E[X(t)] = µ= a const.
(ii) R(t1, t2) = a fy of (t 1 - t2) The
auto covariance fn is gn by

Which depends only on the time
difference. Hence X(t) is covariance stationary.
If X(t) is a wide sense stationary
process with auto correlation R ()τ =Ae−α(),
determine the second order moment of the
random variable X(8) - X(5).
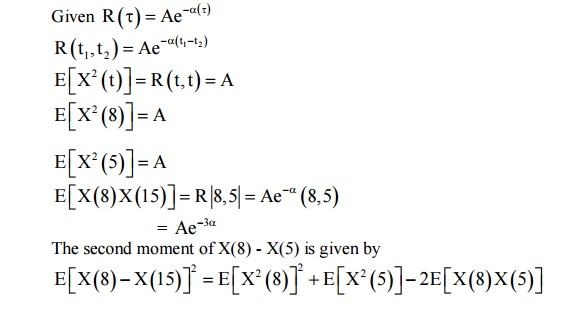
The
second moment of X(8) - X(5) is given by
= A
+ A - 2Ae-3α
= 2A(1–e–3α)


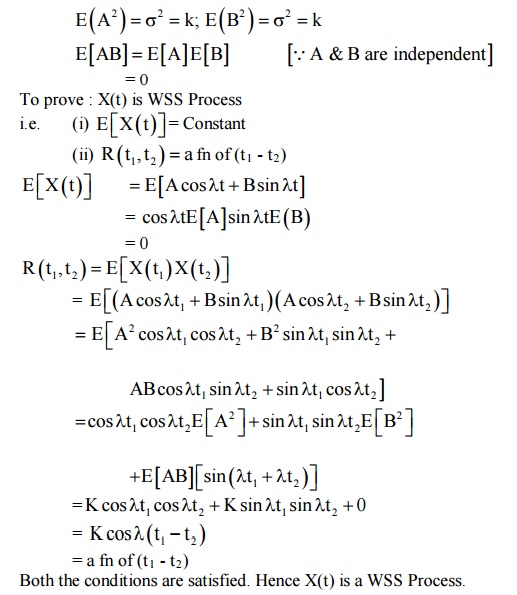

CROSS CORRELATION
The cross correlation of the two random process {X(t)} and {Y(t)} is defined by RXY (t1, t2) = E[X(t1) Y (t2)]
WIDE - SENSE STATIONARY (WSS)
A random process {X(t)} is called a weakly stationary process or covariance stationary process or wide-sense stationary process if
i) E{X(t)} = Constant
ii) E[X(t) X(t+τ] = Rxx(τ) depend only on τ when τ = t2 - t1.
REMARKS :
SSS Process of order two is a WSS Process and not conversely.
EVOLUTIONARY PROCESS
A random process that is not stationary in any sense is called as evolutionary process.
SOLVED PROBLEMS ON WIDE SENSE STATIONARY PROCESS
Example:3.6.1
Given an example of stationary random process and justify your claim.
Solution:
Let us consider a random process X(t) = A as (wt + θ) where A &ω are custom and 'θ' is uniformlydistribution random Variable in the interval (0, 2π).
Since 'θ' is uniformly distributed in (0, 2π), we have


Hence Poisson process is not a stationary process.
Ergodic Process are
processes for which time and ensemble (statistical) averages are
interchangeable the concept of ergodicity deals with the equality of time and
statistical average.
Time
Average

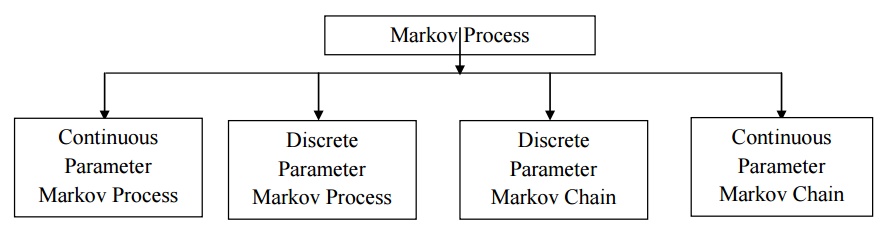
MARKOV
PROCESS - MARKOV CHAINS
1
Markov Process
A
random process X(t) is said to be Markov Process, it
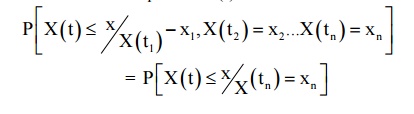
2
Markov Chain
A
discrete parameter Markov Process is called Markov Chain.


Example
:3.4.1
An Engineering
analysing a series of digital signals generated by a testing system observes
that only 1 out of 15 highly distorted signals followed a highly distorted
signal with no recognizable signal, where as 20 out of 23 recognizable signals
follow recognizable signals with no highly distorted signals b/w. Given that
only highly distorted signals are not recognizable. Find the fraction of
signals that are highly distorted.
π1= The fraction of signals that are recognizable [R]
π2 =
The fraction of signals that are highly distorted [D]






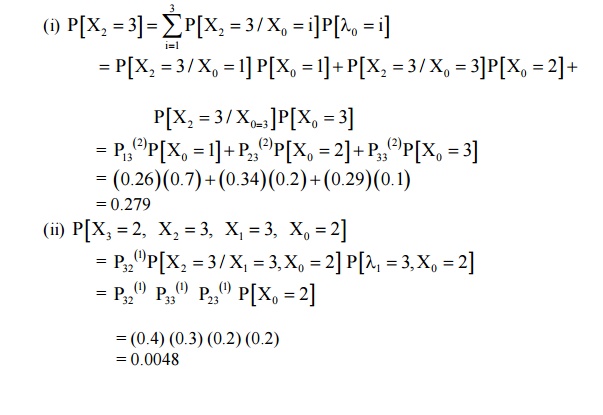
TYPE 5
A training process is
considered as two State Markov Chain. If it rain, it is considered to be state
0 & if it does not rain the chain is in stable 1. The tmp of the Markov
Chain is defined as
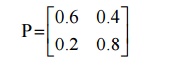
i. Find the Prob. That it will rain for 3
days from today assuming that it is raining
today.
ii. Find also the
unconditional prob. That it will rain after 3 days with the initial Prob. Of
state ) and state 1 as 0.4 & 0.6 respectively.


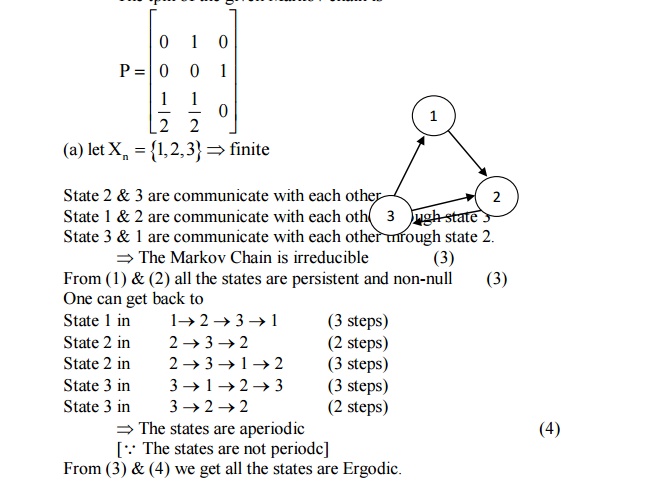
Three boys A, B, C are
throwing a ball each other. A always throws the ball to B & B always throws
the ball to C but C is just as like to throw the ball to B as to A. State that
the process is Markov Chain. Find the tpm and classify the status.
ERGODIC RANDOM PROCESS
Time Average
The time average of a random process {X(t)} is defined as
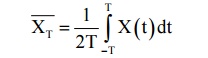
Ensemble Average
The ensemble average of a random process {X(t)} is the expected value of the random variable X at time t
Ensemble Average = E[X(t)]
Ergodic Random Process
{X(t)} is said to be mean Ergodic

Mean Ergodic Theorem
Let {X(t)} be a random process with constant mean µ and let XT be its time average. Then {X(t)} is mean ergodic if
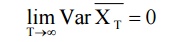
Correlation Ergodic Process
The stationary process {X(t)} is said to be correlation ergodic if the process {Y(t)} is mean ergodic where
Y(t) = X(t) X(t+λ)

MARKOV PROCESS
Definition
A random process {X(t)} is said to be markovian if
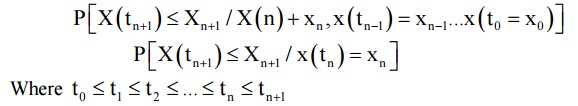
Examples of Markov Process
1.The probability of raining today depends only on previous weather conditions existed for the last two days and not on past weather conditions.
2.A different equation is markovian.
Classification of Markov Process
MARKOV CHAIN
Definition
We define the Markov Chain as follows
If P{Xn = an/Xn-1 = an-1, Xn-2 = an-2, … X0 = a0}
⇒P{Xn = an / Xn-1 = an-1} for all n. the process {Xn}, n = 0, 1, 2… is called as Markov Chains.
1.a1, a2, a3, … an are called the states of the Markov Chain.
2.The conditional probability P{X n = aj | X n −1 = ai} = Pij (n −1, n) is called the one step
transition probability from state a i to state a j at the nth step. 3.The tmp of a Markov chain is a stochastic matricx
i) Pij≥ 0
ii) ΣPij = 1 [Sum of elements of any row is 1]
Poisson Process
The Poisson Process is a continuous parameter discrete state process which is very useful model for many practical situations. It describe number of times occurred. When an experiment is conducted as a function of time.
Property Law for the Poisson Process
Let λ be the rate of occurrences or number of occurrences per unit time and Pn(t) be the probability of n occurrences of the event in the interval (0, t) is a Poisson distribution with parameter λt.
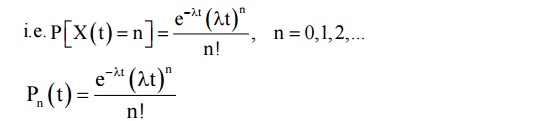

SEMI RANDOM TELEGRAPH SIGNAL PROCESS
If N(t) represents the number of occurrence of a specified event in (0, t) and X(t) = (–)N(t), then {X(t)} is called a semi-random telegraph signal process.
1 RANDOM TELEGRAPH SIGNAL PROCESS
Definition
A random telegraph process is a discrete random process X(t) satisfying the following:
i. X(t) assumes only one of the two possible values 1 or –1 at any time 't'
ii. X(0) = 1 or –1 with equal probability 1/2
iii. The number of occurrence N(t) from one value to another occurring in any interval of length 't' is a Poisson process with rate λ, so that the probability of exactly 'r' transitions is
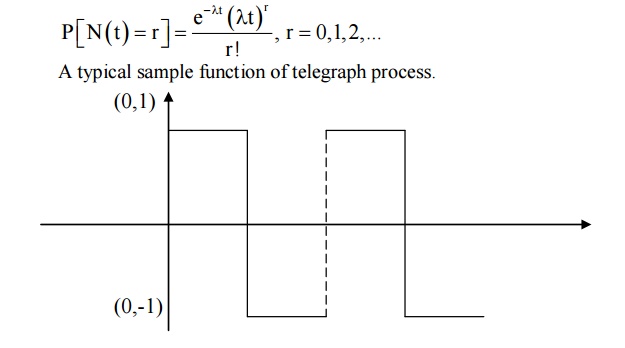
Note: The process is an example for a discrete random process.
* Mean and Auto Correlation P{X(t) = 1} and P{X(t) = 1" for any t.
POISSON BINOMIAL PROCESS
If X(t) represents the
no. of occurrences of certain even in (0, t), then the discrete random process
{X(t)} is called the Poisson process, provided the following postulate are
satisfied.
i.
P[1 occurrence in (t, t+∆t)
= λ∆t
ii.
P[0 occurrence in (t, t+∆t)
= 1 - λ∆t
iii.
P[2 occurrence in (t, t+∆t)
= 0
X(t) is independent of the no. of
occurrences of the event in any interval prior and after the interval (0, t)
v. The Prob. That the
events occurs a specified no. of times in (t0, t0+t) depends only on t, but not
on t0.
Prob. Law for the Poisson Process {X(t)}

BINOMIAL PROCESS
Let Xn, n = 1, 2, 3, … be a Bernoulli
Process and Sn denote the No. of the
successes in the 1st n Bernoulli trails i.e., S

Example:3.7.1
Suppose that customers arrive at a bank
according to a Poisson Process with mean rate of 3 per minute. Find the Prob.
That during a time interval of 2 minutes (i) exactly 4 customer arrive(ii)Greater
than 4 customer arrive (iii) Fewer than 4 customer arrive.

Example:3.7.2
If customers arrive at a counter in
accordance with a Poisson process with a mean rate of 2 per minute, find the
Prob. that the interval 6/w two consecutive arrivals is (i) more than 1 minute
(ii) B/W 1 & 2 minute (iii) 4 minutes or less
λ= 2
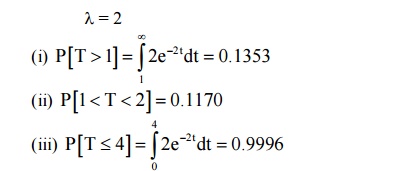
TUTORIAL QUESTIONS
1.. The t.p.m of a Marko cain with three states 0,1,2 is P and the initial state distribution is Find (i)P[X2=3] ii)P[X3=2, X2=3, X1=3, X0=2]
2. Three boys A, B, C are throwing a ball each other. A always throws the ball to B and B always throws the ball to C, but C is just as likely to throw the ball to B as to A. S.T. the process is Markovian. Find the transition matrix and classify the states
3. A housewife buys 3 kinds of cereals A, B, C. She never buys the same cereal in successive weeks. If she buys cereal A, the next week she buys cereal B. However if she buys P or C the next week she is 3 times as likely to buy A as the other cereal. How often she buys each of the cereals?
4. A man either drives a car or catches a train to go to office each day. He never goes 2 days in a row by train but if he drives one day, then the next day he is just as likely to drive again as he is to travel by train. Now suppose that on the first day of week, the man tossed a fair die and drove to work if a 6 appeared. Find 1) the probability that he takes a train on the 3rd day. 2). The probability that he drives to work in the long run.


Related Topics