Important Short Objective Question and Answers: Random Variables

Random Variable

1.. Define Random Variable (RV).

A random variable is a function X: S → R that assigns a real number X(S) to every element s ∈ S , where S is the sample space corresponding to a random experiment E.

Ex: Consider an experiment of tossing an unbiased coin twice. The outcomes of the experiment are HH, HT, TH,TT.let X denote the number of heads turning up. Then X has the values 2,1,1,0. Here X is a random variable which assigns a real number to every outcome of a random experiment.

2. Define Discrete Random Variable.

If X is a random variable which can take a finite number or countably infinite number of pvalues, X is called a discrete RV.

Ex. Let X represent the sum of the numbers on the 2 dice, when two dice are trown.

3. Define Continuous Random Variable.

If X is a random variable which can take all values (i.e., infinite number of values) in an interval, then X is called a continuous RV.

Ex. The time taken by a lady who speaks over a telephone.

4. Define One-dimensional Random Variables.

If a random variable X takes on single value corresponding to each outcome of the experiment, then the random variable is called one-dimensional random variables.it is also called as scalar valued RVs.

Ex:

In coin tossing experiment, if we assume the random variable to be appearance of tail, then the sample space is{H,T} and the random variable is{1,0}.which is an one-dimensional random variables.

5. State the Properties of expectation.

If X and Y are random variables and a,b are constants, then 1.E(a)=a

Proof:

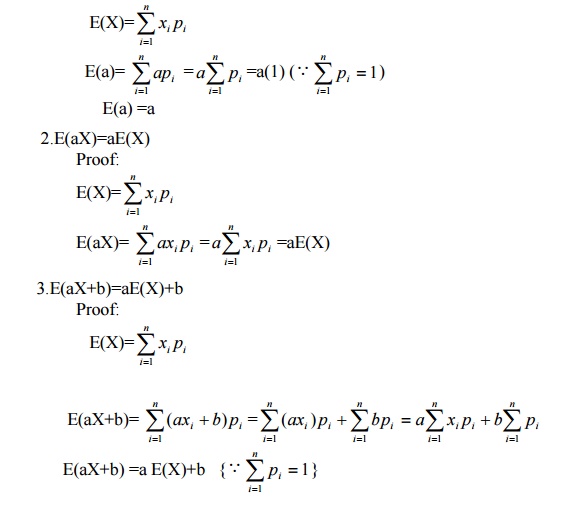
4.E(X+Y)=E(X)+E(Y)                                                                                          

5. E(XY)=E(X).E(Y), if X and Y are random variables.

6. A RV X has the following probability function

1) Determine the

2) Find P(X<3), P(X ≥ 3), P(0<X<5).

Solution:

a+3a+5a+7a+9a+11a+13a+15a+17a=1 81a = 1

a = 1/81

2)   P(X<3) = P(X=0) + P(X=1) +P(X=2) 

= a+3a+5a

=9a =9/81=1/9

P(X ≥ 3) = 1- P(X<3) =1-1/9 = 8/9

P(0<X<5) = P(X=1) + P(X=2) + P(X=3) +P(X=4)

3a+5a+7a +9a =24a= 24/81

7.If X is a continuous RV whose PDF is given by

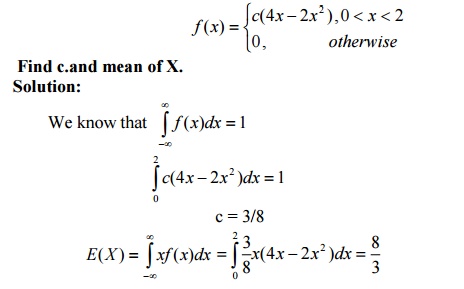
8. A continuous RV X that can assume any value between x = 2 and x = 5 has a density function given by f (x) = k(1+ x).Fnd P(X<4).

Solution:

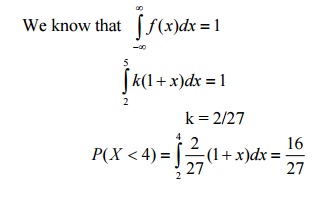
9. A RV X has the density function

12. Determine the Binomial distribution whose mean is 9 and whose SD is 3/2

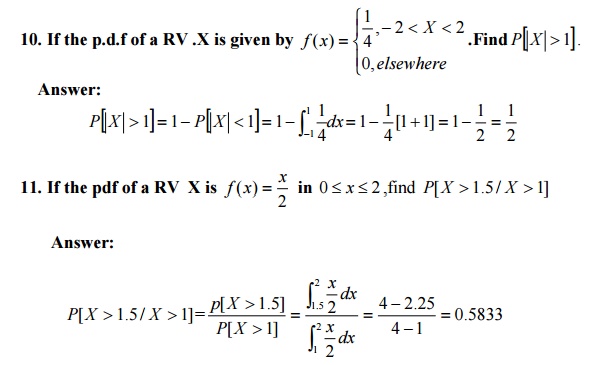
13. Find the M.G.F of a Binomial distribution

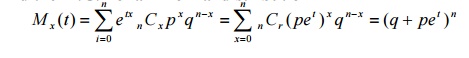
14. The mean and variance of the Binomial distribution are 4 and 3 respectively. Find P(X=0).

mean = np = 4,     Variance = npq = 3

15.     For a Binomial distribution mean is 6 and standard deviation is Rt(2) . Find the first two terms of the distribution.

18. If a R.V X takes the values -1,0,1 with equal probability find the M.G.F of X.

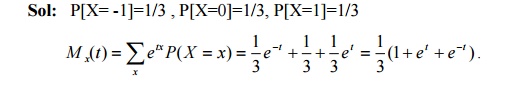
19. A die is thrown 3 times. If getting a 6 is considered as success find the probability of atleast 2 success.

20. Find p for a Binimial variate X if n=6,and 9P(X=4)=P(X=2).

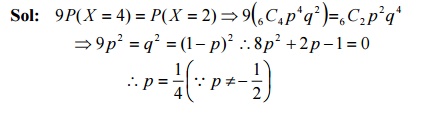
21. Comment on the following

“The mean of a BD is 3 and variance is 4” For B.D, Variance< mean

∴The given statement is wrongs

22.  Define poisson distribution 

A discrete RV X is said to follow Poisson Distribution with parameter λ if its

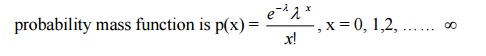
23. If X is a Poisson variate such that P(X=2)=9P (X = 4) + 90 P(X=6), find the variance

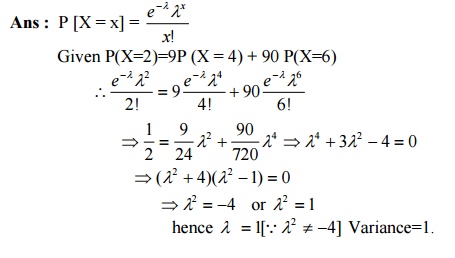
24.  It is known that 5% of the books bound at a certain bindery have defective bindings. find the probability that 2 of 100 books bound by this bindery will have defective bindings. 

Ans : Let X denote the number of defective bindings.

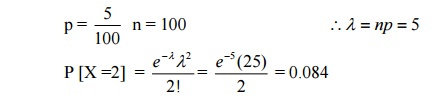
25. Find λ , if X follows Poisson Distribution such that P(X=2)=3P(X=3).

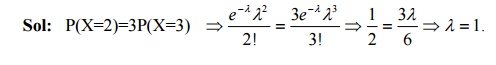
26. If X is a Poisson variate such that P(X = 1) =        3/10 and P(X = 2) =      1/5

Find P(X = 0) and P(X = 3) .

27. For a Poisson Variate X , E(X 2 ) = 6 .What is E(X).

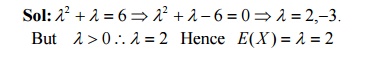
28.A Certain Blood Group type can be find only in 0.05% of the people. If the population of a randomly selected group is 3000.What is the Probability that atleast a people in the group have this rare blood group.

Sol: p=0.05% =0.0005  n=3000       ∴λ = np = 1.5       

P(X ≥ 2) = 1− P(X < 2) = 1− P(X = 0) − P(X = 1)         

29. If X is a poisson variate with mean λ show that E[X2] = λ E[X+1]

E[X2] = λ2 + λ

E (X+1) = E[X] + 1

E[X 2 ] = λE[X +1]

30. Find the M.G.F of Poisson Distribution.

Ans :

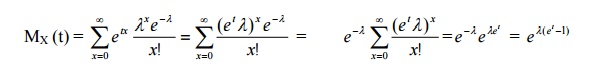
31. A discrete RV X has M.G.F Mx(t) = e2(et −1) . Find E (X), var (X) and P(X=0)

Ans :MX(t) = e2(et −1) ⇒ X follows Poisson Distribution ∴λ = 2

Mean = E (X) = λ = 2               

Var (X) = λ = 2

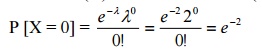
32. If the probability that a target is destroyed on any one shot is 0.5, what is the probability that it would be destroyed on 6th attempt?

Ans : Given p = 0.5 q = 0.5 By Geometric distribution

P [X =x] = qx p, x = 0,1,2………

since the target is destroyed on 6th attempt x = 5 ∴Required probability = qx p = (0.5)6 = 0.0157

33. Find the M.G.F of Geometric distribution

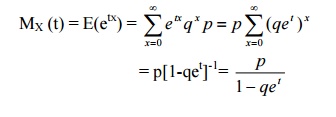
34. Find the mean and variance of the distribution P[X=x]=2-x, x=1,2,3….

Solution:

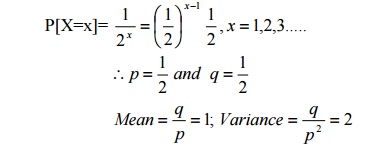
35. Find the expected value and the variance of the number of times one must throw a die

until the outcome 1 has occurred 4 times.

Solution:

X follows the negative bionomial distribution with parameter r = 4 and p=1/6

E(X)= mean = r P = rqQ = r (1-p) (1/p)= 20. (p=1/Q and q=P/Q) Variance = rPQ = r(1-p)/p2 = 120.

36.  If a boy is throwing stones at a target, what is the probability that his 10th throw is his 5th hit, if the probability of hitting the target at any trial is ½? 

Solution:

Since 10th throw should result in the 5th successes ,the first 9 throws ought to have resulted in 4 successes and 5 faliures.

n = 5,r = 5, p = 1/2 = q

∴Required probability = P(X=5)= (5+5-1)C5 (1/2)5 (1/2)5

=9C4 (1/210) = 0.123

37. Find the MGF of a uniform distribution in (a, b)?

Ans :

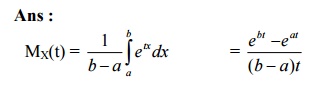
38. Find the MGF of a RV X which is uniformly distributed over (-2, 3)

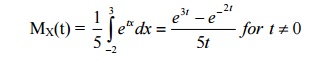
39. The M.G.F of a R.V X is of the form Mx (t) = (0.4et + 0.6)8 what is the M.G.F of 

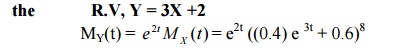
40. If X is uniformly distributed with mean 1 and variance 4/3 find P(X<0)

Ans :Let X follows uniform distribution in (a,b) mean

∴a+b = 2 

(b-a)2 = 16 ⇒ b - a = ± 4

Solving we get a=-1 b=3

41. A RV X has a uniform distribution over (-4, 4) compute P(|X|>2)

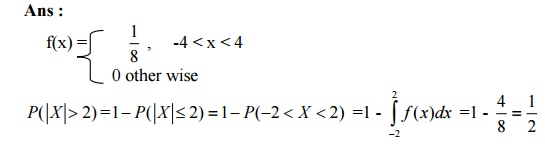
52.What are the properties of Normal distribution 

(i) The normal curve is symmetrical when p = q or p ≈ q. 

(ii)             The normal curve is single peaked curve.

(iii) The normal curve is asymptotic to x-axis as y decreases rapidly when x increases numerically.

(iv) The mean, median and mode coincide and lower and upper quartile are equidistant from the median.

(v)The curve is completely specified by mean and standard deviation along with the value yo. 

53.Write any four properties of normal distribution. 

Sol:  (1) The curve is Bell shaped

(2)Mean, Median, Mode coincide 

(3)All odd moments vanish 

 (4)x - axis is an asymptote of the normal curve 

54.If X is a Normal variate with mean30 and SD 5.Find P [26<X<40].

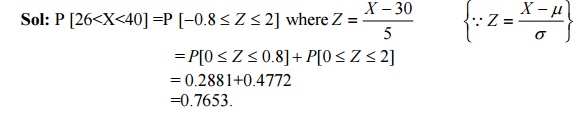
55. If X is normally distributed RV with mean 12 and SD 4.Find P [X ≤ 20].

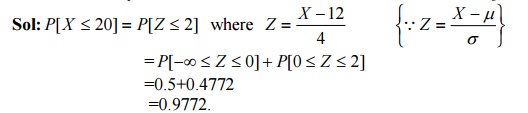
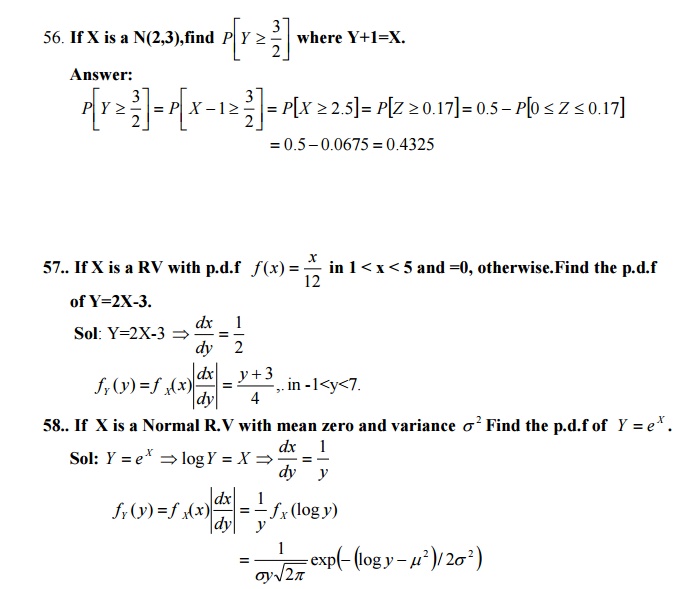
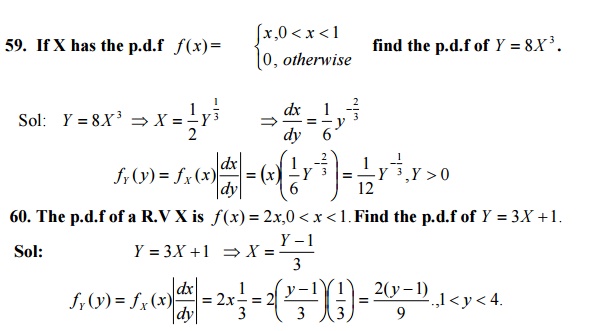
Moment generating functions

1. Define nth Moments about Origin

The nth moment about origin of a RV X is defined as the expected value of the nth power of X.

For discrete RV X, the nth moment is defined as E(X n ) = ∑ xi n pi = µn′,n ≥ 1