Chapter: Electrical and electronics : Circuit Theory : Resonance and Coupled Circuits
The step response of series RLC circuit
Details
about the step response of series RLC circuit
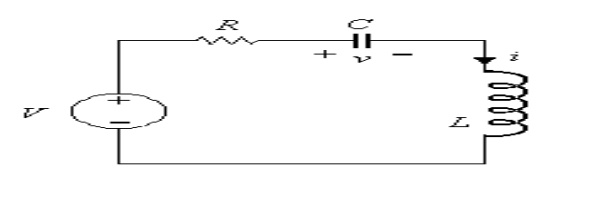
In series RLC circuit, there are two energy storing
element which are L and C, such a circuit give rise to second order
differential equation and hence called second order circuit.
Consider a series RLC circuit shown in Figure. The
switch is closed at t = 0 and a step voltage of V volts gets applied to
circuit.
Apply KVL after
switching we get
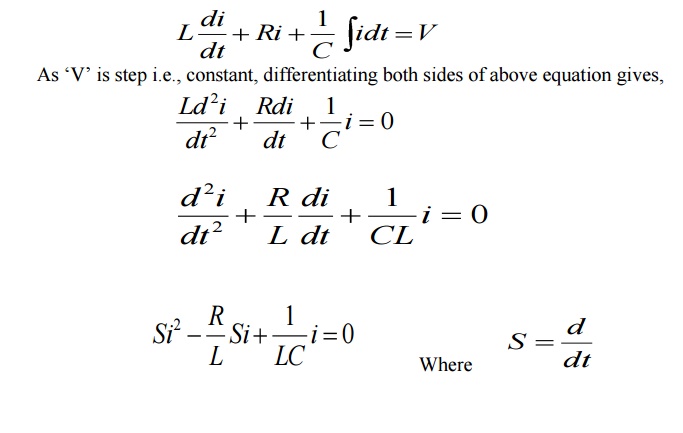
This is called characteristic equation or auxiliary
equation of series RLC circuits.
The response of the
circuit depends on the nature of the roots of characteristic equation. The two
roots are,
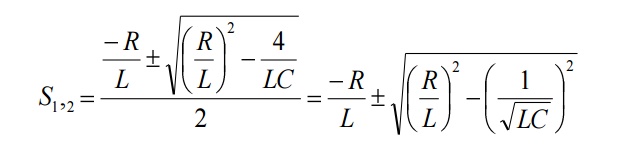
Let us define some
quantities to find the response according to the nature of roots.
Critical resistance :-
This is the value of
resistance which reduces square root term to zero, giving real, equal and
negative roots.
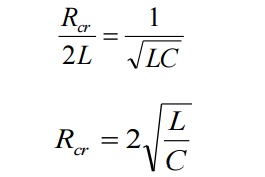
Damping Ratio (ξ):-
The ratio is the indication of
opposition from the circuit to cause oscillations in its response more the
value of this ratio, less are the chances of oscillations in the response. It
is the ratio of actual resistance in the circuit to critical resistance.
It is denoted
by zeta(ξ),
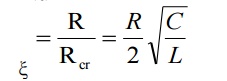
3. Natural:
(ω)
If the damping is made
zero then the response oscillates with natural frequency without any
opposition. Such a frequ Frequency of oscillations,.Itisgivenby denoted as ω
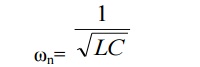
Using these values, the
roots of equation are
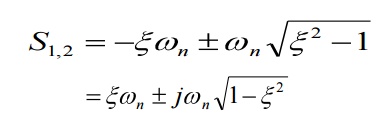
Thus the response is totally dependent
on the Let n α = ξ ω
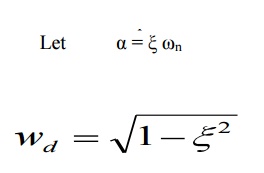
Where wd = actual frequency of oscillations (i.e)
damped frequency when ξ = 0,
wd = ωn (i.e.) natural frequency.
The general solution of
characteristic equation is
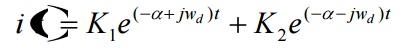
Related Topics