The Stable Marriage Problem

The Stable Marriage Problem

In this section, we consider an interesting version of bipartite matching called the stable marriage problem. Consider a set Y = {m₁, m₂, . . . , m_n} of n men and a set X = {w₁, w₂, . . . , w_n } of n women. Each man has a preference list ordering the women as potential marriage partners with no ties allowed. Similarly, each woman has a preference list of the men, also with no ties. Examples of these two sets of lists are given in Figures 10.11a and 10.11b. The same information can also be presented by an n × n ranking matrix (see Figure 10.11c). The rows and columns of the matrix represent the men and women of the two sets, respectively. A cell in row m and column w contains two rankings: the first is the position (ranking) of w in the m’s preference list; the second is the position (ranking) of m in the w’s preference list. For example, the pair 3, 1 in Jim’s row and Ann’s column in the matrix in Figure 10.11c indicates that Ann is Jim’s third choice while Jim is Ann’s first. Which of these two ways to represent such information is better depends on the task at hand. For example, it is easier to specify a match of the sets’ elements by using the ranking matrix, whereas the preference lists might be a more efficient data structure for implementing a matching algorithm.

A marriage matching M is a set of n (m, w) pairs whose members are selected from disjoint n-element sets Y and X in a one-one fashion, i.e., each man m from

        is paired with exactly one woman w from X and vice versa. (If we represent

and X as vertices of a complete bipartite graph with edges connecting possible marriage partners, then a marriage matching is a perfect matching in such a graph.)

A pair (m, w), where m ∈ Y, w ∈ X, is said to be a blocking pair for a marriage matching M if man m and woman w are not matched in M but they prefer each other to their mates in M. For example, (Bob, Lea) is a blocking pair for the marriage matching M = {(Bob, Ann), (Jim, Lea), (Tom, Sue)} (Figure 10.11c) because they are not matched in M while Bob prefers Lea to Ann and Lea prefers Bob to Jim. A marriage matching M is called stable if there is no blocking pair for it; otherwise, M is called unstable. According to this definition, the marriage matching in Figure 10.11c is unstable because Bob and Lea can drop their designated mates to join in a union they both prefer. The stable marriage problem is to find a stable marriage matching for men’s and women’s given preferences.

Surprisingly, this problem always has a solution. (Can you find it for the instance in Figure 10.11?) It can be found by the following algorithm.

Stable marriage algorithm

Input: A set of n men and a set of n women along with rankings of the women by each man and rankings of the men by each woman with no ties allowed in the rankings

Output: A stable marriage matching

Step 0 Start with all the men and women being free.

Step 1 While there are free men, arbitrarily select one of them and do the following:

Proposal The selected free man m proposes to w, the next woman on his preference list (who is the highest-ranked woman who has not rejected him before).

Response If w is free, she accepts the proposal to be matched with m. If she is not free, she compares m with her current mate. If she prefers m to him, she accepts m’s proposal, making her former mate free; otherwise, she simply rejects m’s proposal, leaving m free.

Step 2 Return the set of n matched pairs.

Before we analyze this algorithm, it is useful to trace it on some input. Such an example is presented in Figure 10.12.

Let us discuss properties of the stable marriage algorithm.

THEOREM The stable marriage algorithm terminates after no more than n² iterations with a stable marriage output.

PROOF The algorithm starts with n men having the total of n² women on their ranking lists. On each iteration, one man makes a proposal to a woman. This reduces the total number of women to whom the men can still propose in the future because no man proposes to the same woman more than once. Hence, the algorithm must stop after no more than n² iterations.

Let us now prove that the final matching M is a stable marriage matching. Since the algorithm stops after all the n men are one-one matched to the n women, the only thing that needs to be proved is the stability of M. Suppose, on the contrary, that M is unstable. Then there exists a blocking pair of a man m and a woman w who are unmatched in M and such that both m and w prefer each other to the persons they are matched with in M. Since m proposes to every woman on his ranking list in decreasing order of preference and w precedes m’s match in M, m must have proposed to w on some iteration. Whether w refused m’s proposal or accepted it but replaced him on a subsequent iteration with a higher-ranked match, w’s mate in M must be higher on w’s preference list than m because the rankings of the men matched to a given woman may only improve on each iteration of the algorithm. This contradicts the assumption that w prefers m to her final match in M.

The stable marriage algorithm has a notable shortcoming. It is not “gender neutral.” In the form presented above, it favors men’s preferences over women’s preferences. We can easily see this by tracing the algorithm on the following instance of the problem:

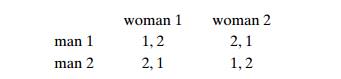
The algorithm obviously yields the stable matching M = {(man 1, woman 1), (man 2, woman 2)}. In this matching, both men are matched to their first choices, which is not the case for the women. One can prove that the algorithm always yields a stable matching that is man-optimal: it assigns to each man the highest-ranked woman possible under any stable marriage. Of course, this gender bias can be reversed, but not eliminated, by reversing the roles played by men and women in the algorithm, i.e., by making women propose and men accept or reject their proposals.

There is another important corollary to the fact that the stable marriage algorithm always yields a gender-optimal stable matching. It is easy to prove that a man (woman)-optimal matching is unique for a given set of participant preferences. Therefore the algorithm’s output does not depend on the order in which the free men (women) make their proposals. Consequently, we can use any data structure we might prefer—e.g., a queue or a stack—for representing this set with no impact on the algorithm’s outcome.

The notion of the stable matching as well as the algorithm discussed above was introduced by D. Gale and L. S. Shapley in the paper titled “College Admissions and the Stability of Marriage” [Gal62]. I do not know which of the two applications mentioned in the title you would consider more important. The point is that stability is a matching property that can be desirable in a variety of applications. For example, it has been used for many years in the United States for matching medical-school graduates with hospitals for residency training. For a brief history of this application and an in-depth discussion of the stable marriage problem and its extensions, see the monograph by Gusfield and Irwing [Gus89].

Exercises 10.4

Consider an instance of the stable marriage problem given by the following ranking matrix:

For each of its marriage matchings, indicate whether it is stable or not. For the unstable matchings, specify a blocking pair. For the stable matchings, indicate whether they are man-optimal, woman-optimal, or neither. (Assume that the Greek and Roman letters denote the men and women, respectively.)

            Design a simple algorithm for checking whether a given marriage matching is stable and determine its time efficiency class.

            Find a stable marriage matching for the instance given in Problem 1 by apply-ing the stable marriage algorithm

            in its men-proposing version.

            in its women-proposing version.

Find a stable marriage matching for the instance defined by the following ranking matrix:

            Determine the time-efficiency class of the stable marriage algorithm

            in the worst case.

            in the best case.

            Prove that a man-optimal stable marriage set is always unique. Is it also true for a woman-optimal stable marriage matching?

            Prove that in the man-optimal stable matching, each woman has the worst partner that she can have in any stable marriage matching.

            Implement the stable-marriage algorithm given in Section 10.4 so that its running time is in O(n²). Run an experiment to ascertain its average-case efficiency.

            Write a report on the college admission problem (residents-hospitals assign-ment) that generalizes the stable marriage problem in that a college can accept “proposals” from more than one applicant.

            Consider the problem of the roommates, which is related to but more difficult than the stable marriage problem: “An even number of boys wish to divide up into pairs of roommates. A set of pairings is called stable if under it there are no two boys who are not roommates and who prefer each other to their actual roommates.” [Gal62] Give an instance of this problem that does not have a stable pairing.

SUMMARY

The iterative-improvement technique involves finding a solution to an op-timization problem by generating a sequence of feasible solutions with improving values of the problem’s objective function. Each subsequent so-lution in such a sequence typically involves a small, localized change in the previous feasible solution. When no such change improves the value of the objective function, the algorithm returns the last feasible solution as optimal and stops.

Important problems that can be solved exactly by iterative-improvement algorithms include linear programming, maximizing the flow in a network, and matching the maximum possible number of vertices in a graph.

The simplex method is the classic method for solving the general linear programming problem. It works by generating a sequence of adjacent extreme points of the problem’s feasible region with improving values of the objective function.

The maximum-flow problem asks to find the maximum flow possible in a network, a weighted directed graph with a source and a sink.

The Ford-Fulkerson method is a classic template for solving the maximum-flow problem by the iterative-improvement approach. The shortest-augmenting-path method implements this idea by labeling network vertices in the breadth-first search manner.

The Ford-Fulkerson method also finds a minimum cut in a given network.

A maximum cardinality matching is the largest subset of edges in a graph such that no two edges share the same vertex. For a bipartite graph, it can be found by a sequence of augmentations of previously obtained matchings.