Symmetric and Asymmetric Components

Symmetric and Asymmetric Components

Any tensor can be resolved into symmetric and asymmetric components where symmetry or asymmetry is with respect to the diagonal. That is,

each of which have quite a different physical effect.

Asymmetric Transformation

Consider first the displacement due to an asymmetric tensor such as:

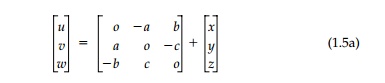
It can be shown to produce a rotation ?= tan^-1 Rt(a² + b² + c² ) 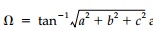  around an axis      whose direction ratios are a, b, and c plus a dilation (a change in size, but not shape). To illustrate, consider the unit square in the x, y plane with b = c = 0

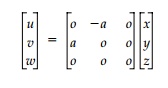
As shown in Figure 1.3, all points rotate in the xy plane an angle ?= tan ^-1 a around the z axis positive in that the rotation vector is in the positive z direction by the right-hand screw rule. Thus the rotation is independent of orientation of the axes in the xy plane and therefore 'invariant.' That is ?_xy=?_ab and the sym-bol ?_z for the rotation vector is sensible although ?_xy is more common in the literature. For 'small' rotations, ?_z = a and the isotropic dilation ( -1 + 1/cos a) is negligible.

Similarly, b and c represent rotation around the y and x axes, respectively. Therefore, the asymmetric displacement tensor can be rewritten

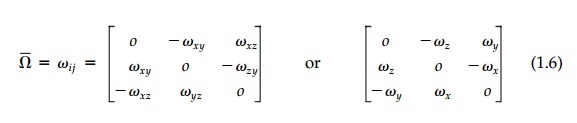
The rotation is not a tensor of second order, but a vector ?Bar = ?_xi + ?_yj + ?_zk made up of three invariant scalar magnitudes in the subscripted directions.

Symmetric Transformation

The symmetric component of a linear displacement tensor can similarly be understood by simple physical examination of the individual elements. Con-sider first the diagonal terms a, b, and c in the symmetric tensor:

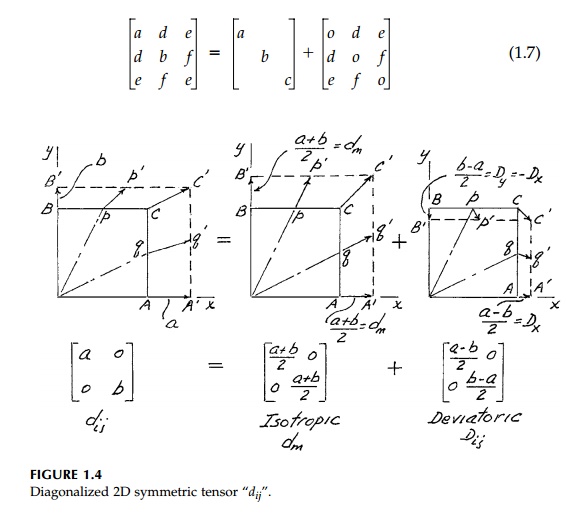
Clearly they produce expansion (contraction if negative) in the xyz directions proportional to the distance from the origin. The 2D case is shown in Figure 1.4, which also illustrates how the effect of the diagonal terms can be further decomposed into two components that are distinctly different physically. In 3D:

where the isotropic component producing pure volume change and no distortion is actually a scalar (tensor of order zero) in which dm =          a + b + c     / 3. The so-called deviatoric component terms:

sum to zero and produce pure distortion and secondary volume change.* For 'small' displacements, the volume change, ?V, is simply 3d_m and the deviatoric volume change is negligible. The subscript, o, is to emphasize the linear superposition is valid for large displacements only if the components are successively applied to the original position vector (base lengths) as is customary in engineering.

Returning to Figure 1.4, it might appear that since individual points (or lines) such as p, q, or c rotate, the deviatoric component is rotational. This is not true and, in fact, symmetric transformations are also called irrotational (and reciprocal). This is illustrated in Figure 1.5 where the diagonal deviatoric transformation components, D_ij, of Figure 1.4 are applied to the second quadrant as well as

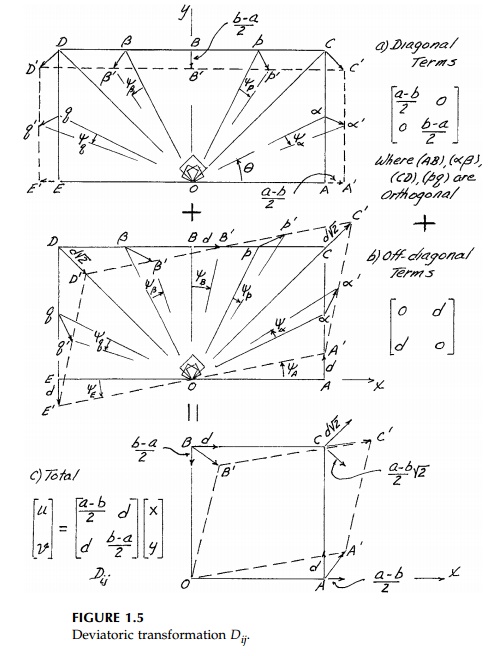
the first (plotted at twice the scale for clarity). The lower two quadrants would be similar.

Thus, line rotations are compensating and there is no net rotation of any pair of orthogonal directions (such as xy, pq, ??, or CD) or for any reflected pair of lines. Any square element, since it is bounded by orthogonal lines, does not rotate either and, for small displacements, its volume will not change. It will undergo pure distortion (change in shape). Certain lines (directions) do not rotate in themselves (in this case, xy) and are termed principal directions while those 45 o from them (OC and OD), undergo the maximum compensating angle change.* The angle change itself (in radians) is called the shear and is consid-ered positive if the 90 o angle at the origin decreases.

Now consider the off-diagonal symmetric terms. The 2D case is shown in Figure 1.5b. Again there is distortion of the shape and, therefore, the off-diagonal symmetric terms are also deviatoric (shear). In this case the lines that do not rotate (principal) are the C-D orthogonal pair and maximum rotation is in the x-y orientation. Thus, again, the maximum and minimum are 45 o apart, just as they were for the diagonal deviatoric terms. In fact, it is easy to show that the diagonal and the off-diagonal terms produce the identical physical effect 45 o out

of phase if b-a/2=d. With either set of deviatoric terms, diagonal or off-diagonal, the element expands in one direction while it contracts an equal amount at right angles. If the element boundaries are not in the principal directions, they rotate in compensating fashion and square shapes become rhomboid. The combined effects on an element of the total deviatoric component is shown in Figure 1.5c. Any isotropic component would simply expand or contract the element.

Extension to 3D is straightforward conceptually, but difficult to draw. The components of the general 3D symmetric transformation will be reviewed in terms of strain and fully defined in terms of stress in the next pages.