Finite Linear Transformation

Finite Linear Transformation

When a body is loaded, the original coordinates of all the points move to a new position. The movement of each point A, B, or C to A'B'C' in Figure 1.1 is the movement of the position vectors r₁ , r₂ , and (r_{1 Bar}  r₂ Bar) where we assume a common origin. A linear transforation is defined as one that transforms vec-tors according to the rules.*

where [a] is the 'finite linear transformation tensor.' Also,

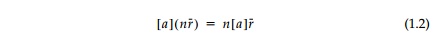
and:

a.  straight lines remain straight

b.  parallel lines remain parallel

c.   parallel planes remain parallel

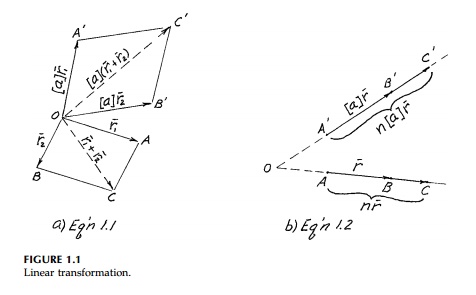
Equations (1.1) and (1.2) are illustrated in Figures 1.1(a) and (b) where n is some constant.

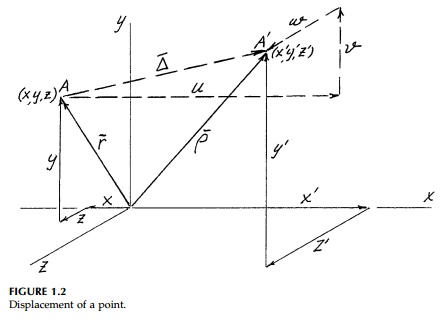
Consider a point A, with Cartesian coordinates x, y, z, which can be thought of as a position or radius vector from the origin as in Figure 1.2. This vector can be written

On linear transformation, this point moves to a new position A' with new coordinates x', y', z'. This transformation can be written in various forms as

Of these, a and b are the most cumbersome and time consuming to use but they are graphic. They emphasize that we are simply dealing with simulta-neous equations. Moreover, they are global and, if linear, the coefficients [a] which are the components of a real, physical transformation tensor must be constant and not themselves functions of x, y, z since if any of the coefficients involve x, y, or z, the equations would have cross products or powers of x, y, z and be nonlinear. Tensor or indicial notation is the most efficient, but only after years of writing out the implied equations does one get a physical feel for this powerful shorthand.

Instead of transforming coordinates of a point (position vectors), it is usu-ally more fruitful in mechanics to talk about how much the coordinates change (i.e., the movement of the tip of the position vector). In fact, it will turn out that if we can find the movement or displacement of all the points of a body, we can easily determine all the strains and usually the stresses caus-ing them. As seen in Figure 1.2, the displacement vector Del Bar of point A moving to A' has components in the x, y, z directions, which are usually called u, v, w in engineering. That is,