Principal or Eigen value Representation

Principal or Eigen value Representation

Under a general linear transformation, all points in a body are displaced such that while straight lines remain straight, most rotate while they also change in length. However, as we have seen, certain directions (lines) 'transform upon themselves' (or parallel to themselves if not from the origin) without rotation and the general tensor must reduce to the special, simple scalar form:

For a nontrivial solution to Equation (1.9), the determinant of the coeffi-cients must equal zero. Expanding this determinant gives 'the characteristic equation'*

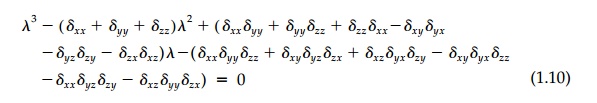
The three roots (real or imaginary-some of which may be equal) are called 'eigenvalues' each with its own eigenvector or characteristic direction. Once the roots are determined, they each can be substituted back into Equation (1.9) to find the corresponding direction r_i = x_ii + y_ij + z_ik.

There are a number of remarkable aspects to this characteristic equation. Perhaps the most important is the invariant nature of the coefficients. The three roots (?₁, ?₂, ?₃) diagonalize the general transformation for one special orientation of axes. However, the choice of initial coordinate system is com-pletely arbitrary. Thus the coefficients must be invariant. That is:

The overriding importance of these invariant directions will become appar-ent when we discuss the strain and stress tensors.

For the general displacement transformation tensor, ?_ij, with a rotation

component, the invariant directions given by the eigenvectors r₁ Bar, r₂ Bar, r₃ Barfor each root ?₁, ?₂, ?₃ need not be orthogonal. However, for the symmetric, d_ij, component (nonrotational), the roots are real and the three invariant directions are orthogonal. They are called principal (principal values and prin-cipal directions perpendicular to principal planes). The search for this principal representation, which diagonalizes a symmetric tensor to the prin-cipal values and reduces the invariants to their simplest forms, is crucial to a physical understanding of stress, strain, or any other second-order tensor.

To summarize this brief introduction of linear transformations, we have seen that:

a.  Under linear transformation, geometric shapes retain their basic identity: straight lines remain straight, parallel lines remain paral-lel, ellipses stay elliptic, and so forth.

b.  However, such linear transformations may involve:

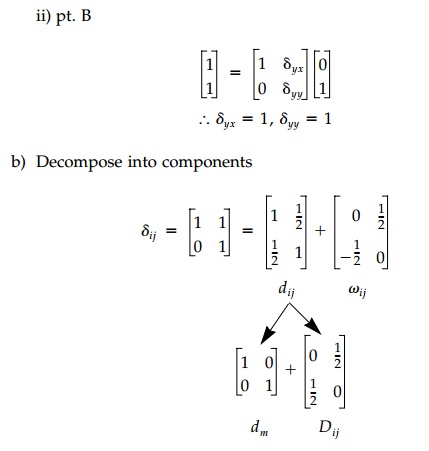
(i)  Volume change (isotropic effect), d_m,

(ii)  Distortion due to compensating angle change (shear or devi-atoric effect), D_ij, and

(iii) Rotation, ?_ij.

c.  These three effects can be seen separately if the general tensor _ij is decomposed into component parts: ?_ij = d_m = D_ij + ?_ij as illus-trated in Example 1.1.

d.  The invariant 'tensor' quality of a linear transformation is expressed in the coefficients of the characteristic equation, which remain constant for any coordinate system even while the nine individual elements change. Since nature knows no man-made coordinate system, we should expect the fundamental 'laws' or phenomena of mechanics (which deals with tensors of various orders) to involve these invariant and not the individual coordinate-dependent elements.

e.   The roots of this characteristic equation with their orientation in space (i.e., eigenvalues and eigenvectors, which reduce the tensor to its diagonal form) are called 'principal.' If the tensor is sym-metric (i.e., no rotation), the principal directions are orthogonal.

Example 1.1

Using the general definition [Equation (1.4)], determine the linear displace-ment tensor that represents the transformation of the triangular shape ABC into AB'C' as shown below and sketch the components.