Symmetric Key Distribution Using Symmetric Encryption

SYMMETRIC KEY DISTRIBUTION USING SYMMETRIC ENCRYPTION

For symmetric encryption to work, the two parties to an exchange must share the same key, and that key must be protected from access by others. Furthermore, fre- quent key changes are usually desirable to limit the amount of data compromised if an attacker learns the key. Therefore, the strength of any cryptographic system rests with the key distribution technique, a term that refers to the means of deliver- ing a key to two parties who wish to exchange data without allowing others to see the key. For two parties A and B, key distribution can be achieved in a number of ways, as follows:

1.                                       A can select a key and physically deliver it to  B.

2.                                       A third party can select the key and physically deliver it to A and  B.

3.                                       If A and B have previously and recently used a key, one party can transmit the new key to the other, encrypted using the old key.

4.                                       If A and B each has an encrypted connection to a third party C, C can deliver a key on the encrypted links to A and B.

Options 1 and 2 call for manual delivery of a key. For link encryption, this is a reasonable requirement, because each link encryption device is going to be exchang- ing data only with its partner on the other end of the link. However, for end-to-end encryption over a network, manual delivery is awkward. In a distributed system, any given host or terminal may need to engage in exchanges with many other hosts and terminals over time. Thus, each device needs a number of keys supplied dynamically. The problem is especially difficult in a wide-area distributed system.

The scale of the problem depends on the number of communicating pairs that must be supported. If end-to-end encryption is done at a network or IP level, then a key is needed for each pair of hosts on the network that wish to communicate. Thus, if there are N hosts, the number of required keys is [N(N - 1)]/2 . If encryption is done at the application level, then a key is needed for every pair of users or processes that require communication. 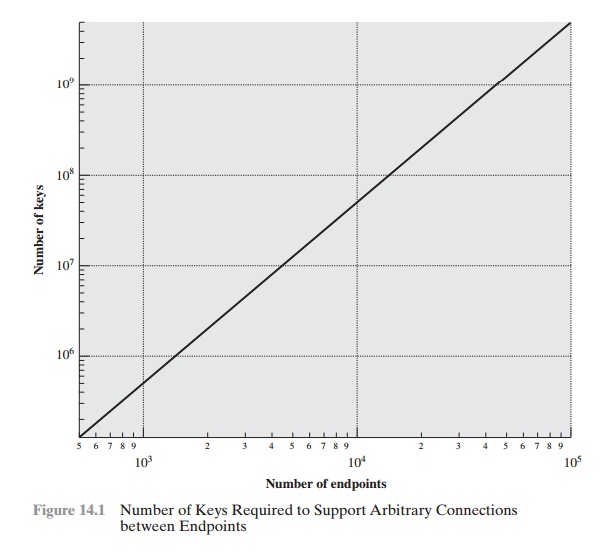Thus, a network may have hundreds of hosts but thousands of users and processes. Figure 14.1 illustrates the magnitude of the

key distribution task for end-to-end encryption.1 A  network using   node-level

encryption with 1000 nodes would conceivably need to distribute as many as half a million keys. If that same network supported 10,000 applications, then as many as 50 million keys may be required for application-level encryption.

Returning to our list, option 3 is a possibility for either link encryption or end- to-end encryption, but if an attacker ever succeeds in gaining access to one key, then all subsequent keys will be revealed. Furthermore, the initial distribution of poten- tially millions of keys still must be made.

For end-to-end encryption, some variation on option 4 has been widely adopted. In this scheme, a key distribution center is responsible for distributing keys to pairs of users (hosts, processes, applications) as needed. Each user must share a unique key with the key distribution center for purposes of key distribution.

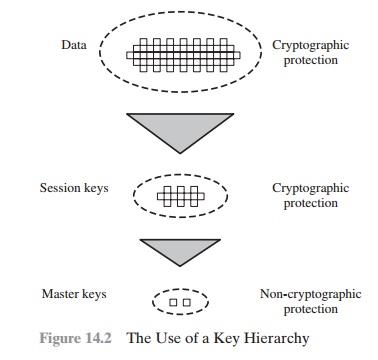
The use of a key distribution center is based on the use of a hierarchy of keys. At a minimum, two levels of keys are used (Figure 14.2). Communication between end systems is encrypted using a temporary key, often referred to as a session key. Typically, the session key is used for the duration of a logical connection, such as a frame relay connection or transport connection, and then discarded. Each session key is obtained from the key distribution center over the same networking facilities used for end-user communication. Accordingly, session keys are transmitted in encrypted form, using a master key that is shared by the key distribution center and an end system or user.

For each end system or user, there is a unique master key that it shares with the key distribution center. Of course, these master keys must be distributed in some fashion. However, the scale of the problem is vastly reduced. If there are N entities that wish to communicate in pairs, then, as was mentioned, as many as [N(N - 1)]/2 session keys are needed at any one time. However, only N master keys are required, one for each entity. Thus, master keys can be distributed in some noncryptographic way, such as physical delivery.

A Key  Distribution Scenario

The key distribution concept can be deployed in a number of ways. A typical sce- nario is illustrated in Figure 14.3, which is based on a figure in [POPE79]. The sce- nario assumes that each user shares a unique master key with the key distribution center (KDC).

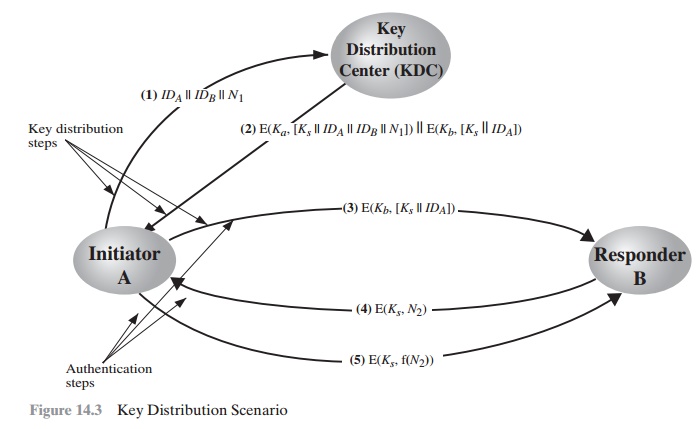
Let us assume that user A wishes to establish a logical connection with B and requires a one-time session key to protect the data transmitted over the connection. A has a master key, Ka, known only to itself and the KDC; similarly, B shares the master key Kb with the KDC. The following steps occur.

1.                                       A issues a request to the KDC for a session key to protect a logical connection to B. The message includes the identity of A and B and a unique identifier, N1, for this transaction, which we refer to as a nonce. The nonce may be a time- stamp, a counter, or a random number; the minimum requirement is that it dif- fers with each request. Also, to prevent masquerade, it should be difficult for an opponent to guess the nonce. Thus, a random number is a good choice for a nonce.

2.                                       The KDC responds with a message encrypted using Ka. Thus, A is the only one who can successfully read the message, and A knows that it originated at the KDC. The message includes two items intended for A:

•                                      The one-time session key, Ks, to be used for the session

•                                      The original request message, including the nonce, to enable A to match this response with the appropriate request

Thus, A can verify that its original request was not altered before reception by the KDC and, because of the nonce, that this is not a replay of some previous request.

In addition, the message includes two items intended for B:

•                                      The one-time session key, Ks, to be used for the session

•                                      An identifier of A (e.g., its network address), IDA

These last two items are encrypted with Kb (the master key that the KDC shares with B).They are to be sent to B to establish the connection and prove A’s identity.

3.                                       A stores the session key for use in the upcoming session and forwards to B the information that originated at the KDC for B, namely, E(Kb,[Ks || IDA]). Because this information is encrypted with Kb, it is protected from eavesdrop- ping. B now knows the session key (Ks), knows that the other party is A (from IDA), and knows that the information originated at the KDC (because it is encrypted using Kb).

At this point, a session key has been securely delivered to A and B, and they may begin their protected exchange. However, two additional steps are desirable:

4.                                       Using the newly minted session key for encryption, B sends a nonce, N2, to A.

5.                                       Also, using Ks, A responds with f(N2) , where f is a function that performs some transformation on N2 (e.g., adding one).

These steps assure B that the original message it received (step 3) was not a replay.

Note that the actual key distribution involves only steps 1 through 3, but that steps 4 and 5, as well as step 3, perform an authentication function.

Hierarchical Key Control

It is not necessary to limit the key distribution function to a single KDC. Indeed, for very large networks, it may not be practical to do so. As an alternative, a hierarchy of KDCs can be established. For example, there can be local KDCs, each responsible for a small domain of the overall internetwork, such as a single LAN or a single building. For communication among entities within the same local domain, the local KDC is responsible for key distribution. If two entities in different domains desire a shared key, then the corresponding local KDCs can communicate through a global KDC. In this case, any one of the three KDCs involved can actually select the key. The hierarchical concept can be extended to three or even more layers, depending on the size of the user population and the geographic scope of the internetwork.

A hierarchical scheme minimizes the effort involved in master key distribu- tion, because most master keys are those shared by a local KDC with its local enti- ties. Furthermore, such a scheme limits the damage of a faulty or subverted KDC to its local area only.

Session Key Lifetime

The more frequently session keys are exchanged, the more secure they are, because the opponent has less ciphertext to work with for any given session key. On the other hand, the distribution of session keys delays the start of any exchange and places a burden on network capacity. A security manager must try to balance these competing considerations in determining the lifetime of a particular session key.

For connection-oriented protocols, one obvious choice is to use the same ses- sion key for the length of time that the connection is open, using a new session key for each new session. If a logical connection has a very long lifetime, then it would be prudent to change the session key periodically, perhaps every time the PDU (protocol data unit) sequence number cycles.

For a connectionless protocol, such as a transaction-oriented protocol, there is no explicit connection initiation or termination. Thus, it is not obvious how often one needs to change the session key. The most secure approach is to use a new ses- sion key for each exchange. However, this negates one of the principal benefits of connectionless protocols, which is minimum overhead and delay for each transac- tion. A better strategy is to use a given session key for a certain fixed period only or for a certain number of transactions.

A Transparent Key Control  Scheme

The approach suggested in Figure 14.3 has many variations, one of which is described in this subsection. The scheme (Figure 14.4) is useful for providing end-to- end encryption at a network or transport level in a way that is transparent to the end users. The approach assumes that communication makes use of a connection-ori- ented end-to-end protocol, such as TCP. The noteworthy element of this approach is a session security module (SSM), which may consist of functionality at one protocol layer, that performs end-to-end encryption and obtains session keys on behalf of its host or terminal.

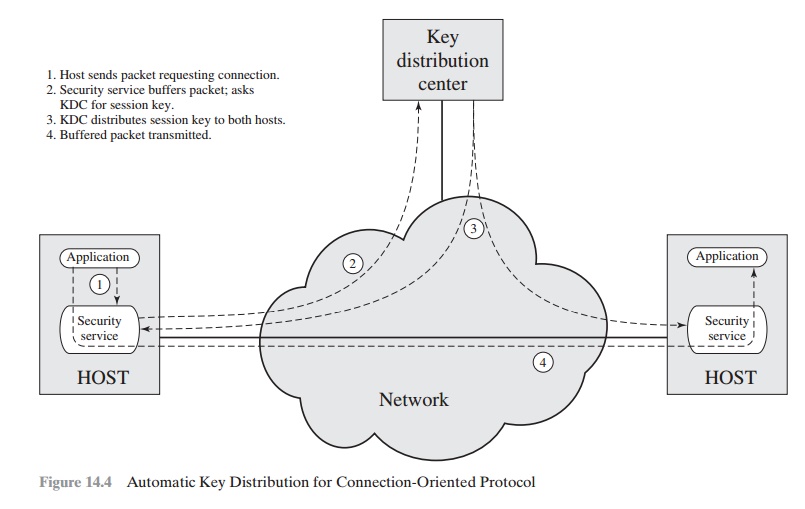
The steps involved in establishing a connection are shown in Figure 14.4. When one host wishes to set up a connection to another host, it transmits a connec- tion-request packet (step 1). The SSM saves that packet and applies to the KDC for permission to establish the connection (step 2). The communication between the SSM and the KDC is encrypted using a master key shared only by this SSM and the KDC. If the KDC approves the connection request, it generates the session key and delivers it to the two appropriate SSMs, using a unique permanent key for each SSM (step 3). The requesting SSM can now release the connection request packet, and a connection is set up between the two end systems (step 4). All user data exchanged between the two end systems are encrypted by their respective SSMs using the one- time session key.

The automated key distribution approach provides the flexibility and dynamic characteristics needed to allow a number of terminal users to access a number of hosts and for the hosts to exchange data with each other.

Decentralized Key Control

The use of a key distribution center imposes the requirement that the KDC be trusted and be protected from subversion. This requirement can be avoided if key distribution is fully decentralized. Although full decentralization is not practical for larger networks using symmetric encryption only, it may be useful within a local context.

A decentralized approach requires that each end system be able to communi- cate in a secure manner with all potential partner end systems for purposes of ses- sion key distribution. Thus, there may need to be as many as [n(n - 1)]/2 master keys for a configuration with n end systems.

A session key may be established with the following sequence of steps (Figure 14.5).

1.                                       A issues a request to B for a session key and includes a nonce, N1.

2.                                       B responds with a message that is encrypted using the shared master key. The response includes the session key selected by B, an identifier of B, the value f(N1), and another nonce, N2.

3.                                       Using the new session key, A returns f(N2) to B.

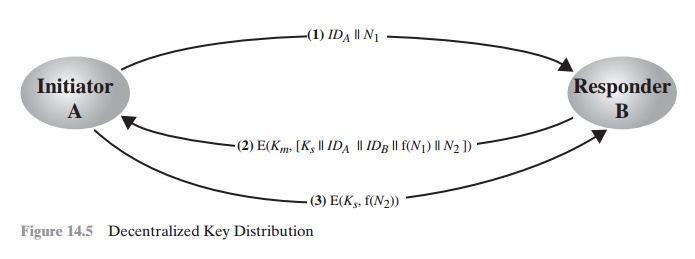
Thus, although each node must maintain at most (n - 1) master keys, as many session keys as required may be generated and used. Because the messages trans- ferred using the master key are short, cryptanalysis is difficult. As before, session keys are used for only a limited time to protect them.

Controlling Key Usage

The concept of a key hierarchy and the use of automated key distribution techniques greatly reduce the number of keys that must be manually managed and distributed. It also may be desirable to impose some control on the way in which automatically distributed keys are used. For example, in addition to separating mas- ter keys from session keys, we may wish to define different types of session keys on the basis of use, such as

•                           Data-encrypting key, for general communication across a network

•                           PIN-encrypting key, for personal identification numbers (PINs) used in elec- tronic funds transfer and point-of-sale applications

•                           File-encrypting key, for encrypting files stored in publicly accessible   locations

To illustrate the value of separating keys by type, consider the risk that a master key is imported as a data-encrypting key into a device. Normally, the mas- ter key is physically secured within the cryptographic hardware of the key distrib- ution center and of the end systems. Session keys encrypted with this master key are available to application programs, as are the data encrypted with such session keys. However, if a master key is treated as a session key, it may be possible for an unauthorized application to obtain plaintext of session keys encrypted with that master key.

Thus, it may be desirable to institute controls in systems that limit the ways in which keys are used, based on characteristics associated with those keys. One simple plan is to associate a tag with each key ([JONE82]; see also [DAVI89]). The pro- posed technique is for use with DES and makes use of the extra 8 bits in each 64-bit DES key. That is, the eight non-key bits ordinarily reserved for parity checking form the key tag. The bits have the following interpretation:

•                           One bit indicates whether the key is a session key or a master key.

•                           One bit indicates whether the key can be used for encryption.

•                           One bit indicates whether the key can be used for decryption.

•                           The remaining bits are spares for future use.

Because the tag is embedded in the key, it is encrypted along with the key when that key is distributed, thus providing protection. The drawbacks of this scheme are

1.                                       The tag length is limited to 8 bits, limiting its flexibility and  functionality.

2.                                       Because the tag is not transmitted in clear form, it can be used only at the point of decryption, limiting the ways in which key use can be controlled.

A more flexible scheme, referred to as the control vector, is described in [MATY91a and b]. In this scheme, each session key has an associated control vector

consisting of a number of fields that specify the uses and restrictions for that session key. The length of the control vector may vary.

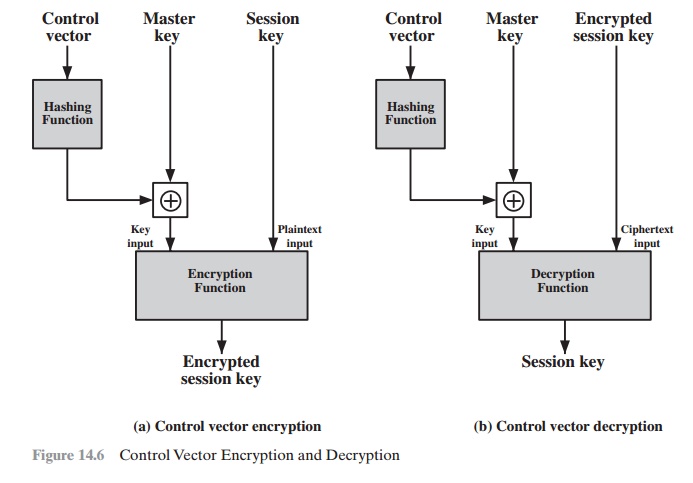
The control vector is cryptographically coupled with the key at the time of key generation at the KDC. The coupling and decoupling processes are illustrated in Figure 14.6. As a first step, the control vector is passed through a hash function that produces a value whose length is equal to the encryption key length. Hash functions are discussed in detail in Chapter 11. In essence, a hash function maps values from a larger range into a smaller range with a reasonably uniform spread. Thus, for example, if numbers in the range 1 to 100 are hashed into numbers in the range 1 to 10, approximately 10% of the source values should map into each of the target values.

The hash value is then XORed with the master key to produce an output that is used as the key input for encrypting the session key. Thus,

Hash value = H = h(CV)

Key input = Km Ⓧ H

Ciphertext = E([Km Ⓧ H], Ks)

where Km is the master key and Ks is the session key. The session key is recovered in plaintext by the reverse operation:

D([Km Ⓧ H], E([Km Ⓧ H], Ks))

When a session key is delivered to a user from the KDC, it is accompanied by the control vector in clear form. The session key can be recovered only by using both the master key that the user shares with the KDC and the control vector. Thus, the linkage between the session key and its control vector is maintained.

Use of the control vector has two advantages over use of an 8-bit tag. First, there is no restriction on length of the control vector, which enables arbitrarily com- plex controls to be imposed on key use. Second, the control vector is available in clear form at all stages of operation. Thus, control of key use can be exercised in multiple locations.