Symmetric Key Distribution Using Asymmetric Encryption

SYMMETRIC KEY DISTRIBUTION USING ASYMMETRIC ENCRYPTION

Because of the inefficiency of public key cryptosystems, they are almost never used for the direct encryption of sizable block of data, but are limited to relatively small blocks. One of the most important uses of a public-key cryptosystem is to encrypt secret keys for distribution. We see many specific examples of this in Part Five. Here, we discuss general principles and typical  approaches.

Simple Secret Key  Distribution

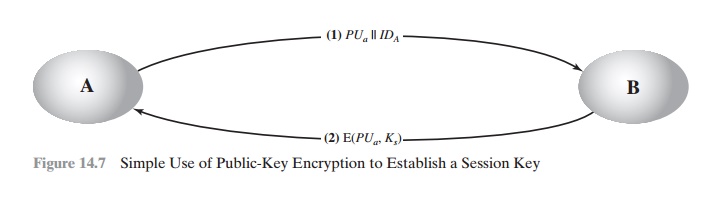
An extremely simple scheme was put forward by Merkle [MERK79], as illustrated in Figure 14.7. If A wishes to communicate with B, the following procedure is employed:

1.                                       A generates a public/private key pair {PUa, PRa} and transmits a message to B consisting of PUa and an identifier of A, IDA.

2.                                       B generates a secret key, Ks, and transmits it to A, which is encrypted with A’s public key.

3.                                       A computes D(PRa, E(PUa, Ks)) to recover the secret key. Because only A can decrypt the message, only A and B will know the identity of Ks.

4.                                       A discards PUa and PRa and B discards PUa.

A and B can now securely communicate using conventional encryption and the session key Ks. At the completion of the exchange, both A and B discard   Ks.

Despite its simplicity, this is an attractive protocol. No keys exist before the start of the communication and none exist after the completion of communication. Thus, the risk of compromise of the keys is minimal. At the same time, the communication is secure from eavesdropping.

The protocol depicted in Figure 14.7 is insecure against an adversary who can intercept messages and then either relay the intercepted message or substitute another message (see Figure 1.3c). Such an attack is known as a man-in-the-middle attack [RIVE84]. In this case, if an adversary, E, has control of the intervening com- munication channel, then E can compromise the communication in the following fashion without being detected.

1.                                       A generates a public/private key pair {PUa, PRa} and transmits a message intended for B consisting of PUa and an identifier of A, IDA.

2.                                       E intercepts the message, creates its own public/private key pair {PUe, PRe} and transmits PUe || IDA  to B.

3.                                       B generates a secret key, Ks, and transmits E(PUe, Ks) .

4.                                       E intercepts the message and learns Ks by computing D(PRe, E(PUe, Ks)).

5.                                       E transmits E(PUa, Ks) to A.

The result is that both A and B know Ks and are unaware that Ks has also been revealed to E. A and B can now exchange messages using Ks. E no longer actively interferes with the communications channel but simply eavesdrops. Knowing Ks, E can decrypt all messages, and both A and B are unaware of the problem. Thus, this simple protocol is only useful in an environment where the only threat is eavesdropping.

Secret Key Distribution with Confidentiality and Authentication

Figure 14.8, based on an approach suggested in [NEED78], provides protection against both active and passive attacks. We begin at a point when it is assumed that A and B have exchanged public keys by one of the schemes described subsequently in this chapter. Then the following steps occur.

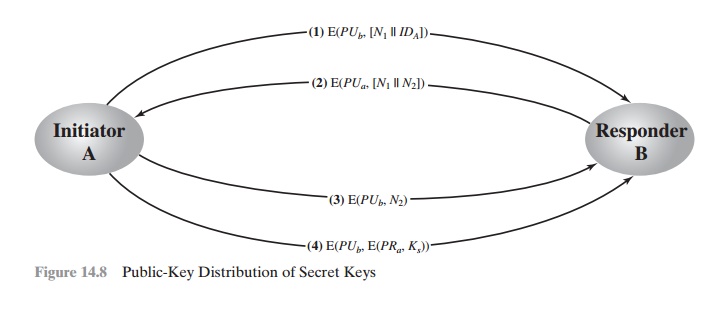
1.                                       A uses B’s public key to encrypt a message to B containing an identifier  of A(IDA) and a nonce (N1), which is used to identify this transaction uniquely.

B sends a message to A encrypted with PUa and containing A’s nonce (N1) as ell as  a  new nonce generated by B (N2). Because  only  B  could have (N2). Because  only  B  could have decrypted message (1), the presence of N1 in message (2) assures A that the correspondent is B.

2.                                       A returns N2, encrypted using B’s public key, to assure B that its correspondent is A.

A selects a secret key Ks and sends M = E(PUb, E(PRa, Ks)) to B. Encryption of this message with B’s public key ensures that only B can read it; encryption

with A’s private key ensures that only A could have sent it.

3.                                       B computes D(PUa, D(PRb, M)) to recover the secret key.

4.                                       The result is that this scheme ensures both confidentiality and authentication in the exchange of a secret key.

A Hybrid Scheme

Yet another way to use public-key encryption to distribute secret keys is a hybrid approach in use on IBM mainframes [LE93]. This scheme retains the use of a key distribution center (KDC) that shares a secret master key with each user and distributes secret session keys encrypted with the master key. A public key scheme is used to distribute the master keys. The following rationale is provided for using this three-level approach:

•                           Performance: There are many applications, especially transaction-oriented applications, in which the session keys change frequently. Distribution of ses- sion keys by public-key encryption could degrade overall system performance because of the relatively high computational load of public-key encryption and decryption. With a three-level hierarchy, public-key encryption is used only occasionally to update the master key between a user and the KDC.

•                           Backward compatibility: The hybrid scheme is easily overlaid on an existing KDC scheme with minimal disruption or software  changes.

The addition of a public-key layer provides a secure, efficient means of distrib- uting master keys. This is an advantage in a configuration in which a single KDC serves a widely distributed set of users.