Subtraction of Integers

Subtraction of Integers

Let us learn subtraction of integers using number line.

Let us try to subtract integers using the number line activity we studied earlier. We should follow the same instructions as before but whenever we need to subtract, we turn towards the negative side.

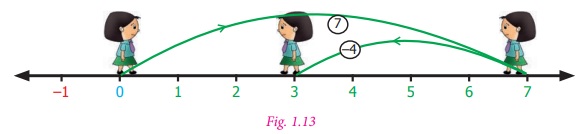
To subtract (+4) from (+7)

We start at zero facing positive direction. Moves 7 units forward to represent +7 then turn towards the negative side for the operation of subtraction and move +4 units forward to represent +4. We reach the integer +3. So, (+7) − (+4) = +3 .

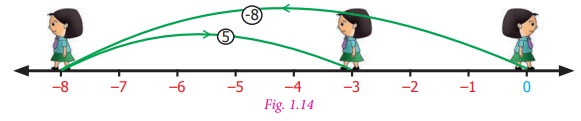
Let us find (−8) − (−5).

We start at zero facing positive direction. Move 8 units backward to represent (–8). Then turn towards the negative side and move 5 units backwards. We reach –3. We have (−8) −(−5) = (–3).

Now, let us learn subtraction of integers in another way.

Observe the following patterns :

7−2=5; 7−1=6; 7−0=7

What will happen if we extend this to negative integers?

7−(−1)= 8; 7 −(−2) = 9; 7 −(−3) = 10

We shall see some more patterns.

20−2 =18; 20−1=19; 20−0 = 20; 20−(−1)= 21; 20 −(−2) = 22

We can see from the above patterns that while subtracting consecutive negative integers from 7 and 20 the difference increase consecutively.

It is clear that subtraction of negative integers gives increase in the difference. For example 7-(-2) =9. Hence, subtraction of -2 is equivalent to addition of 2, which is the additive inverse of -2. That is, 7+2 =9.

So, to subtract a negative integer from an integer we add the additive inverse of the integer which is to be subtracted.

For example, subtract (-5) from 7.

7 − (-5)

To subtract (-5) we can add additive inverse of (-5) that is 5 with 7

Therefore, 7 – (–5) = 12

Try these

1. Do the following by using number line.

(i) (–4)–(+3) ;

(–4) – (+3) = –7

(ii) (–4)–(–3)

(–4) – (–3) = –4 + 3 = –1

2. Find the values and compare the answers.

(i) (–6)–(–2) and (–6)+2

 (–6) – (–2), –6 + 2 = –4

–6 + 2 = –4

(–6) – (–2) = (–6) + 2

They are equal

(ii) 35–(–7) and 35 + 7

35 – (–7) = 35 + 7 = 42

35 + 7 = 42

35 – (–7) = 35 + 7

They are equal 

(iii) 26 –(+10) and 26 + (–10)

26 – (+10) = 26 – 10 = 16

26+ (–10) = 26– 10 = 16

26 – (+10) = 26 + (–10)

They are euqal

3. Put the suitable symbol <, > or = in the boxes.

(i) −10 − 8 ___ −10 +8

(ii) (−20) + 10 ___ (−20) − (−10)

(iii) (−70) − (−50) ___  (−70) −50

(iv) 100 − (+100) ___  100 − (−100)

(v) −50 −30  ___  −100 + 20

(i) – 10 – 8 < – 10 + 8

(ii) (–20) + 10  = –20 – (–10)

(iii) (–70) – (–50)  > (–70) – 50

(iv) 100 – (+100)  < 100– (–100)

(v) –50 – 30 = –100 + 20

Note

Every subtraction statement has a corresponding addition statement. For example, 8 − 5 = 3 is a subtraction statement. This can be seen as the addition statement 3 + 5 = 8 In the same way, (−8) − (−5) = −3 is a subtraction statement which can be written as the addition statement ( −8) = ( −3) + ( −5) .

Example 1.10

Subtract the following using the number line.

(i) –3 – (–2) (ii) +6 – (–5)

Solution

(i) –3 – (–2)

To subtract –2 from –3 using number line,

Therefore, –3 – (–2) = –3 + 2 = –1

(ii) +6 – (–5)

To subtract –5 from 6 using number line,

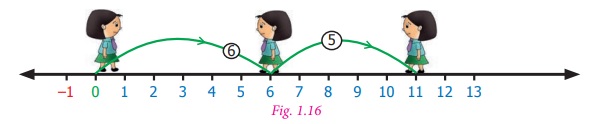
Therefore, +6 – (–5) = +6 + 5 = 11.

Now, let us see how to subtract negative integers using additive inverse.

Example 1.11

(i) Subtract ( −40) from 70

(ii) Subtract ( −12) from ( −20)

Solution

(i) 70 − ( −40)

= 70 + (additive inverse of −40 )

= 70 + 40

= 110.

(ii) ( −20) − ( −12)

= ( −20) + (additive inverse of ( −12) )

= (−20)+12

 = – 8

Example 1.12

Find the value of : (i) ( −11) − ( −33) (ii) (−90) − ( −50)

Solution

(i) ( −11) − ( −33)

= (−11)+ (+33)

= 22

(ii) (−90) − ( −50)

= −90 −(−50)

= −90+50

= −40

Example 1.13

Chitra has ₹ 150. She wanted to buy a bag which costs ₹ 225. How much money does she need to borrow from her friend?

Solution

Amount with Chitra = ₹ 150

Cost of bag = ₹ 225

Amount to be borrowed = ₹ 225 − ₹ 150

= ₹75

Example 1.14

What is the balance in Chezhiyan’s account as a result of a purchase for ₹ 1079, if he had an opening balance of ₹ 5000 in his account?

Solution

Opening balance = ₹ 5000

Debit amount = ₹ 1079 (−)

Balance amount = ₹ 3921

Example 1.15

The temperature at Srinagar was −3°C on Friday. If the temperature decreases by 1°C next day, then what is the temperature on that day?

Solution

The temperature at Srinagar was −3°C on Friday. If the temperature decreases by 1°C then, temperature on the next day = −3°C – 1°C = −4°C

Example 1.16

A submarine is at 300 feet below the sea level. If it ascends to 175 feet, what is its new position?

Solution

Initial position of submarine = 300 feet below

 = -300 feet

Distance ascended by submarine = 175 feet

 = + 175 feet

New position of submarine = (−300) + (+175)

= −125

That is, the submarine is 125 feet below the sea level.