Properties of Addition

Properties of Addition

In class VI, we have studied that the collection of whole numbers is closed under the addition operation. The sum of two whole numbers is always a whole number. Does this property hold for the collection of integers also?

Complete the given table and check whether the sum of two integers is an integer or not?

We observe that in all the above cases the sum of two integers is an integer. Since addition of integers is an integer, we say that integers are closed under addition. This property is known as "closure property" of integers on addition.

Therefore, for any two integers a, b; a+b is also an interger.

We observe one more property of integers. The order in which we add two integers does not matter. For example, 12 + ( −13) is the same as ( −13) + (12) . Also ( −7) + ( −5) is the same as ( −5) + (−7) .

This property is known as “commutative property” of integers.

Therefore, for any two integers a, b; a+b = b+a.

What happens when we add three integers? For example, will ( −7) + ( −2) + (−9) give the same value when they are added in any way of grouping.

Let us check by grouping the integers as [(–7)+(–2)]+ (–9) and (–7) + [(–2) + (–9)].

First let us find the value of [(–7)+(–2)]+ (–9).

[(–7)+(–2)]+ (–9) = (–9) + (–9) = –9 – 9 = –18

Let us illustrate this with the number line : [( −7) + ( −2)] + ( −9) can be represented as

[ (−7)+ (−2) ] + (−9) = (−18)

 Then we will find the value of (–7) + [(–2) + (–9)]

(–7) + [(–2) + (–9)] = (–7) + (–11) = –7 – 11 = –18

(–7) + [(–2) + (–9)] can be represented on the number line as below.

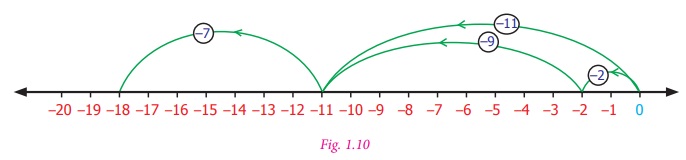
(–7) + [(–2) + (–9)] = (–18)

We reach the same number –18 in both the cases. Hence, regrouping of integers does not change the value of the sum. This property is known as “associative property” under addition.

Therefore, for any three integers a, b, c; a+(b+c) = (a+b)+c

The collection of integers has positive, negative integers and zero. Have you noticed that zero is neither positive nor negative integer. What happens when we add zero to an integer?

For example, we observe that 7+0=7, (–3)+0 = (–3), (–27)+0 = (–27),  (–79)+0 = (–79), 0+(–69) = (–69), 0+(–85) = (–85).

From the above it is clear that whenever zero is added to an integer, we get the same integer. Due to this property, zero is called the identity with respect to addition or "additive identity" of the collection of integers.

Therefore, for any integers a, a+0 = a = 0+a

The additive identity zero separates the number line into positive and negative integers. We have +1 and–1,+5 and –5,–15 and +15, etc. on opposite sides of the number line that are equidistant from zero. Such integers on either side of zero are called “opposites” of each other. In fact, we find that the “opposites” added together always give the value zero.

For example, ( −15) +15 = 0 , 21 + ( −21) = 0 . This property of integers is named as “additive inverse”. (–15) is the additive inverse of 15 because their sum is zero. In the same way, 21 is the additive inverse of  −21 . Either of the pair of opposites is known as the "additive inverse" of the other.

Therefore, for any integer a, –a is the additive inverse.

a+ (–a) = 0 = (–a)+a

Try these

1. Fill in the blanks:

(i) 20 + ( −11) = (–l l) + 20

(ii) (−5) + (−8) = (−8) + (–5)

(iii) (−3) +12 = 12 + (−3)

2. Say true or false.

(i) ( −11) + ( −8) = ( −8) + ( −11) (True)

(ii) −7 + 2 = 2 + ( −7) (True)

(iii) ( −33) + 8 = 8 + ( −33) (True)

(iv) 11 + (–3) = –3 + (11) (True)

(v) –3 + (–9) = –9 + (–3) (True)

3. Verify the following:

(i) [( −2) + ( −9)] + 6 = ( −2) + [(−9) + 6]

[–11] + 6 = –2 + [–3]

–5 = –5 verified

(ii) [7 + ( −8)] + ( −5) = 7 + [(−8) + ( −5)]

[7–8] + (–5) = 7 + [–8 + –5]

–1 + –5 = 7 – 13

–6 = –6

verified

(iii) [(−11)+ 5] + (−14) = (−11)+ [5 + (−14)]

(–6) + (–14) = (–l l) + (–9)

–20 = –20

verified

(iv) ( −5) + [( −32) + ( −2)] = [( −5) + ( −32)] + ( −2)

 –5 + (–34) = (–37) + (–2)

–39 = –39

verified

4. Find the missing integers:

(i) 0 + (–95) = –95

(ii) −611 + 0 = −611

(iii) –79 + 0 = –79

(iv) 0 + ( −140) = –140

5. Complete the following:

(i) −603 + 603 = 0

(ii) 9847 + ( −9847) = 0

(iii) 1652 + (–1652) = 0

(iv) −777 + 777 = 0

(v) –5281 + 5281 = 0

Example 1.7

(i) Are 120 + 51 and 51 + 120 equal?

(ii) Are ( −5) + [( −4) + ( −3)] and [( −5) + ( −4)] + ( −3) equal?

Solution

(i) When we add, 120 + 51 = 171 ; 51 + 120 = 171

In both the cases we get same answer. This means that integers can be added in any order. Hence, addition of integers is commutative.

(ii) ( −5) + [( −4) + ( −3)] and [( −5) + ( −4)] + ( −3)

In (–5) +[(–4) +(–3)], (–4) and (–3) are added first and their result is then added with (–5).

 (–5) +[(–4) +(–3)] = –12

Whereas in [( −5) + ( −4)] + ( −3) , (–4) and (–3) are added first and then the result is added with (–5)

 [(–5) +(–4)] + (–3) = – 12

In both the cases, we get −12

That is ( −5) + [( −4) + ( −3)] = [( −5) + (−4)] + (−3)

So, addition is associative.

Example 1.8

Find the missing integers (i) 0 + ( −2345) = ______ (ii) 23479 + _____ = 0

Solution

(i) 0 +  (−2345) = − 2345

(ii) 23479 + (−23479) = 0

Therefore, additive inverse of 23479 is –23479

Example 1.9

Mention the property for the following equations:

(i) (−45)+ (−12) = −57

(ii) (−15)+ 7 = (7)+ (−15)

(iii) −10+3= −7

(iv) (−7)+ (−5) = (−5)+ (−7)

(v) (−7)+ [(−4)+ (−3)] = [(−7)+ (−4)] + (−3)

(vi) 0 + (−7245) = −7245

Solution

(i) Closure Property

(ii) Commutative Property

(iii) Closure Property

(iv) Commutative Property

(v) Associative Property

(vi) Additive Identity