Statistical Evaluation of Measurement Data

STATISTICAL EVALUATION OF MEASUREMENT DATA

Out of the various possible errors, the random errors cannot be determined in the ordinary process of measurements. Such errors are treated mathematically.

The mathematical analysis of the various measurements is called statistical analysis of the data’.

For such statistical analysis, the same reading is taken number of times, generally u sing different observers, different instruments & by different ways of measurement. The statistial aalysis helps to determine analytically t he uncertainty of the final test results.

Arithmetic mean &median:

When the n umber of readings of the same measurement are taken, the most likely value from the set of measured value is the arithmetic mean of the number of readings taken.

The arithmetic mean value can be mathematically obtained as,

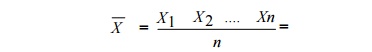
This mean is very close to true value, if number of readings is very large.

But when the number of readings is large, calculation of mean value is complicated. In such a case, a median value is obtained which is obtained which is a close approximation to the arithmetic mean value. For a set of µ Q¶ measurements X1, X2, X3.Xn written down in the ascending order of magnitudes, the median value is given by,

Xmedian = X (n+1)/2

Average deviation:

The deviation tells us about the departure of a given reading from the arithmetic mean of the data set

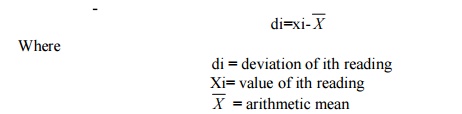
The average deviation is defined as the sum of the absolute values of deviations divided by the number of readings. This is also called mean deviation