Chapter: Electrical and electronics : Circuit Theory : Network Reduction and Network Theorems for DC And AC Circuits
Star Delta Conversion
STAR DELTA CONVERSION:
In many circuit applications, we encounter components connected together in one of two ways to form a three-terminal network: the ŌĆĢDelta or (also the ŌĆĢStar (also known as the ŌĆĢY) configuration
Problem 1: A star-connected load consists of three identical coils each of resistance 30 ╬® and inductance 127.3 mH. If the line current is 5.08 A, calculate the line voltage if the supply frequency is 50 Hz.
Inductive reactance XL =2ŽĆfL
=2ŽĆ(50) (127.3├Ś10ŌłÆ3) =40 ╬®
Impedance of each phase Zp =ŌłÜ(R2 + X2L) =ŌłÜ(302 +402) =50 ╬® For a star connection IL =Ip =VpZp
Hence phase voltage Vp =IpZp = (5.08)(50)=254V Line voltage VL =ŌłÜ3Vp =ŌłÜ3(254) =440V
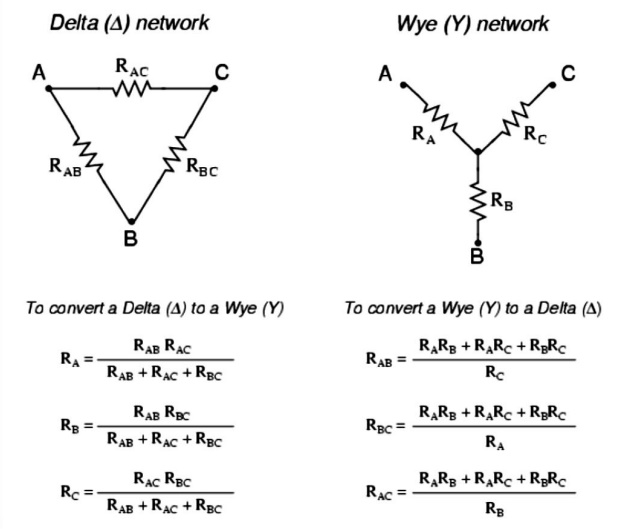
Problem 2: A 415V, 3-phase, 4 wire, star-connected system supplies three resistive loads as shown in Figure Determine (a) the current in each line and (b) the current in the neutral conductor.
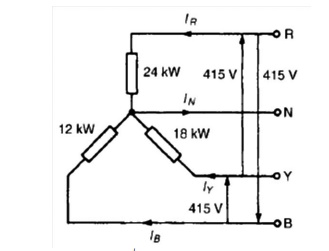
(a) For a star-connected system VL =ŌłÜ3Vp
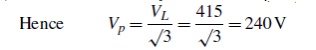
Since current I = Power P/Voltage V for a resistive load then IR = PR/VR= 24 000/240=100A
IY = PY/VY= 18 000/240=75A and IB = PB/VB= 12 000/240=50A
(b) The three line currents are shown in the phasor diagram of Figure Since each load is resistive the currents are in phase with the phase voltages and are hence mutually displaced by 120ŌŚ”.The current in the neutral conductor is given by:
IN = IR + IY + IB phasorially.
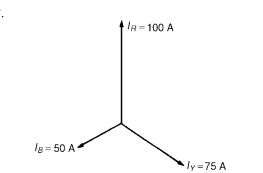
Figure shows the three line currents added phasorially.Oa represents IR in magnitude and direction. From the nose of Oa, ab is drawn representing IY in magnitude and direction. From the nose of ab, bc is drawn representing IB in magnitude and direction. Oc represents the resultant, IN.
By measurement, IN =43A
ŌŚ” ŌŚ” ŌŚ”
Alternatively, by calculation, considering IR at 90 , IB at 210 and IY at 330 :
ŌŚ” ŌŚ” ŌŚ”
Total horizontal component = 100 cos 90 + 75 cos 330 +50 cos 210 = 21.65
ŌŚ” ŌŚ” ŌŚ”
Total vertical component = 100 sin 90 + 75 sin 330 +50 sin 210 = 37.50
Hence magnitude of IN =ŌłÜ(21.652 + 37.502)
= 43.3A
Problem 3: Convert the given delta fig into equivalent star.
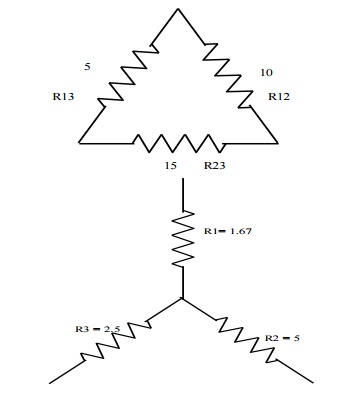
R1 = R12xR13/R12+R13+R23
R1 = 10x5/30 = 1.67Ōä”
R2 = 10 x 15/30 = 5╬®
R3 = 5 x 15/30 = 2.5╬®
Problem 4: Convert the given star in fig into an equivalent delta.
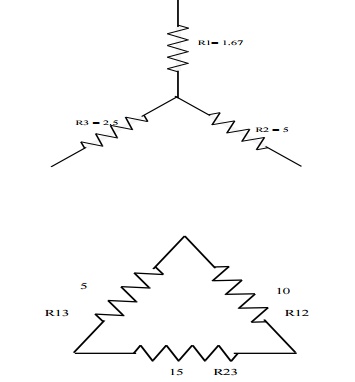
R12 = R1+R2 + R1R2/R3 = 1.67 x 5/2.5 + 1.67+5 = 10╬®
R23 = 2.5+5 2.5x5/1.67 = 15╬®
R31 = 2.5+1.67+ 2.5 x 1.67/5 = 5╬®
Problem 5: Obtain the delta connected equivalent for the star connected circuit.

Problem 6: Obtain the star connected equivalent for the delta connected circuit.
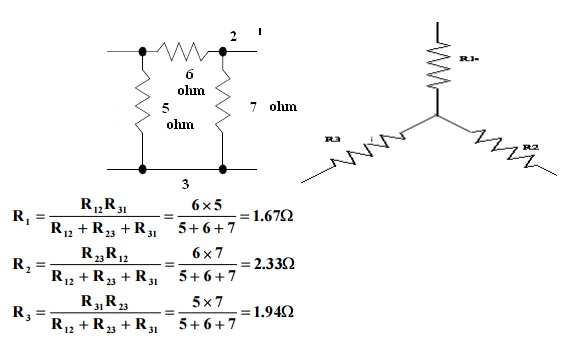
Related Topics