Standardizing Methods: Internal Standards

Internal Standards

The successful application of an external standardization or the method of standard additions, depends on the analyst’s ability to handle samples and standards repro- ducibly. When a procedure cannot be controlled to the extent that all samples and standards are treated equally, the accuracy and precision of the standardization may suffer. For example, if an analyte is present in a volatile solvent, its concentration will increase if some solvent is lost to evaporation. Suppose that you have a sample and a standard with identical concentrations of analyte and identical signals. If both experience the same loss of solvent their concentrations of analyte and signals will continue to be identical. In effect, we can ignore changes in concentration due to evaporation provided that the samples and standards experience an equivalent loss of solvent. If an identical standard and sample experience different losses of solvent, however, their concentrations and signals will no longer be equal. In this case, an external standardization or standard addition results in a determinate error.

A standardization is still possible if the analyte’s signal is referenced to a signal generated by another species that has been added at a fixed concentration to all samples and standards. The added species, which must be different from the ana- lyte, is called an internal standard.

Since the analyte and internal standard in any sample or standard receive the same treatment, the ratio of their signals will be unaffected by any lack of repro- ducibility in the procedure. If a solution contains an analyte of concentration C_A, and an internal standard of concentration, C_IS, then the signals due to the analyte, S_A, and the internal standard, S_IS, are

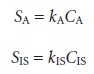
where k_A and k_IS are the sensitivities for the analyte and internal standard, respectively. Taking the ratio of the two signals gives

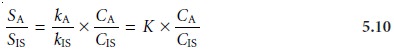
Because equation 5.10 is defined in terms of a ratio, K, of the analyte’s sensitivity and the internal standard’s sensitivity, it is not necessary to independently deter- mine values for either k_A or k_IS.

In a single-point internal standardization, a single standard is prepared, and K is determined by solving equation 5.10

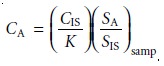
A single-point internal standardization has the same limitations as a single- point normal calibration. To construct an internal standard calibration curve, it is necessary to prepare several standards containing different concentrations of ana- lyte. These standards are usually prepared such that the internal standard’s concen- tration is constant. Under these conditions a calibration curve of (S_A/S_IS)_stand versus C_A is linear with a slope of K/C_IS.

When the internal standard’s concentration cannot be held constant the data must be plotted as (S_A/S_IS)_stand versus C_A/C_IS, giving a linear calibration curve with a slope of K.