Chapter: Modern Analytical Chemistry: Calibrations, Standardizations, and Blank Corrections
Standardizing Methods: External Standards
External Standards
The most commonly employed standardization method
uses one or more external
standards containing known
concentrations of analyte.
These standards are identi-
fied as external standards because
they are prepared
and analyzed separately from the samples.
A quantitative determination using a single
external standard was
described at the beginning
of this section, with k given
by equation 5.3. Once standardized, the concentration of analyte,
CA, is given as
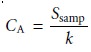 5.4
5.4

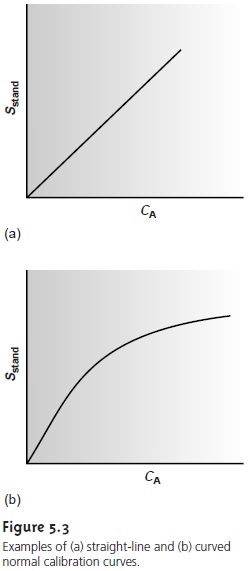
A multiple-point external standardization is accomplished by
constructing a calibration curve, two examples of which are shown in Figure 5.3. Since this is
the most frequently employed method
of standardization, the
resulting relation- ship often is called a normal calibration curve. When the calibration curve is a linear
(Figure 5.3a), the
slope of the
line gives the
value of k. This
is the most
de- sirable situation since
the method’s sensitivity remains constant throughout the standard’s concentration
range. When the calibration curve is nonlinear, the method’s sensitivity is a function of the analyte’s concentration. In Figure
5.3b, for example, the value of k is greatest
when the analyte’s concentration is small and decreases continuously as the amount
of analyte is increased. The
value of k at any point along the calibration curve is given by the slope at that point. In
either case, the calibration curve
provides a means
for relating Ssamp to the ana- lyte’s concentration.

An external standardization allows a related
series of samples
to be ana- lyzed using a single calibration curve. This is an important advantage in labo- ratories where many samples
are to be analyzed or when the need for a rapid throughput of samples is critical. Not surprisingly, many of the most com- monly encountered quantitative analytical methods are based
on an external standardization.
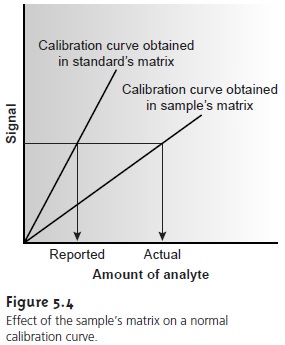
There is a serious limitation, however, to an external standardization. The relationship between Sstand and CS in equation 5.3 is determined when the analyte is present in the external
standard’s matrix. In using an exter- nal
standardization, we assume
that any difference between the matrix
of the standards and the sample’s
matrix has no effect on the value of k. A proportional determinate error is
introduced when differences between the two matrices cannot be ignored. This is shown
in Figure 5.4,
where the re-
lationship between the signal and the amount of analyte is shown for both the sample’s matrix and the
standard’s matrix. In this
example, using a normal calibration curve results in a negative
determinate error. When matrix problems are expected, an effort is made to match the
matrix of the standards to that of the sample.
This is known as matrix matching. When the sample’s
matrix is unknown,
the matrix effect
must be shown
to be negligi- ble, or an alternative method
of standardization must
be used. Both
approaches are discussed in the following sections.
Related Topics