Solved Problems: Design of Temporary and Permanent Joints

A bracket, as shown in Figure, supports a load of 30 kN. Determine the size of bolts, if the maximum allowable tensile stress in the bolt material is 60 MPa. The distances are : L1 = 80 mm, L2 = 250 mm, and L = 500 mm.

Solution.

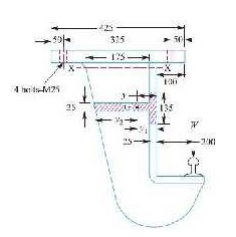
Given :

W = 30 kN

σt = 60 MPa = 60 N/mm2 L1 = 80 mm

L2 = 250 mm L = 500 mm

We know that the direct tensile load carried by each bolt, Wt1 = (W / n)

=30 / 4

=7.5 kN

Load in a bolt per unit distance,

= WL / 2[(L1)² + (L2)²]

=30 x 500 / 2[80² + 250²]

=0.109 kN/mm

Since the heavily loaded bolt is at a distance of L2 mm from the tilting edge, therefore load on the heavily loaded bolt,

Wt2  = w.L2

=0.109 × 250

=27.25 kN

Maximum tensile load on the heavily loaded bolt,

Wt = Wt1 + Wt2

=7.5 + 27.25

34.75 kN = 34750 N

Let dc = Core diameter of the bolts.

We know that the maximum tensile load on the bolt (Wt), 34750 = (π / 4) × (dc)² σt

(dc)² = 34750 / 47 = 740

dc        = 27.2 mm

From Table 11.1 (coarse series), we find that the standard core diameter of the bolt is 28.706 mm and the corresponding size of the bolt is M 33.

Design a sleeve and cotter joint to resist a tensile load of 60 kN. All parts of the joint are made of the same material with the following allowable stresses : σt = 60 MPa ; τ= 70MPa and σc = 125 MPa

Solution.

Given :

σc  = 125 MPa = 125 N/mm2

1. Diameter of the rods

Let d = Diameter of the rods. Considering the failure of the rods in tension.

We know that load (P),

60 × 10³  =   ^π  x d² x σt

4

d² = 60 × 10³/ 47.13 = 1273

= 35.7 say 36 mm

Diameter of enlarged end of rod and thickness of cotter

Let      d2 = Diameter of enlarged end of rod, and

t = Thickness of cotter. It may be taken as d2 / 4.

Considering the failure of the rod in tension across the weakest section (i.e. slot). We know that

load (P),

60 × 10³  = [         ^π (d2)² - d2 x t]

σt

4

= [ ^π (d2)² - d2 x (d2/4)] 60

4

= 32.13 (d2)2

(d2)²  = 60 × 10³ / 32.13 = 1867

d2        = 43.2 say 44 mm

Thickness of cotter,

= (d2/4) = 44/4

=11 mm

Let us now check the induced crushing stress in the rod or cotter. We know that load (P), 60 × 10³ = d2 × t ×σc

=44 × 11 × σc

=484 σc

σc   = 60 × 10³ / 484

= 124 N/mm2

Since the induced crushing stress is less than the given value of 125 N/mm2, therefore the dimensions d2 and t are within safe limits.

3. Outside diameter of sleeve

Let d1 = Outside diameter of sleeve.

Considering the failure of sleeve in tension across the slot.

We know that load (P)

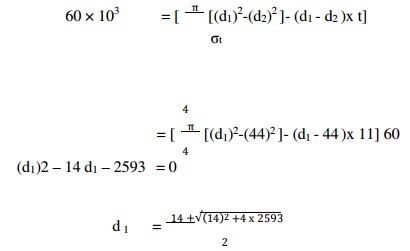
= 58.4 say 60 mm.

4. Width of cotter

Let b = Width of cotter.

Considering the failure of cotter in shear. Since the cotter is in double shear, therefore load (P), 60 × 103 = 2 b × t × τ

=2 × b × 11 × 70

=1540 b

= 60 × 10³ / 1540

= 38.96 say 40 mm

Distance of the rod from the beginning to the cotter hole (inside the sleeve end)

Let a = Required distance.

Considering the failure of the rod end in shear. Since the rod end is in double shear, therefore load (P),

60   10³  = 2 a × d2 × τ

=2 a × 44 × 70

=6160 a

= 60 × 103 / 6160

= 9.74 say 10 mm

Distance of the rod end from its end to the cotter hole

Let c = Required distance.

Considering the failure of the sleeve end in shear. Since the sleeve end is in double shear, therefore load (P),

60 × 10³  = 2 (d1 – d2) c × τ

2 (60 – 44) c × 70

2240 c

= 60 × 10³ / 2240

= 26.78 say 28 mm.

Design a knuckle joint to transmit 150 kN. The design stresses may be taken as 75 MPa in tension, 60 MPa in shear and 150 MPa in compression.

Solution.

Given :

P = 150 kN = 150 × 103 N σt = 75 MPa = 75 N/mm2

= 60 MPa = 60 N/mm2

σc   = 150 MPa = 150 N/mm2

The knuckle joint is shown in Fig. 12.16. The joint is designed by considering the various methods of failure as discussed below:

1. Failure of the solid rod in tension

Let d = Diameter of the rod.

We know that the load transmitted (P),

d² = 150 × 10³ / 59 = 2540 d = 50.4 say 52 mm

Now the various dimensions are fixed as follows: Diameter of knuckle pin,

d1 = d = 52 mm

Outer diameter of eye,

d2 = 2d = 2 × 52

= 104 mm

Diameter of knuckle pin head and collar, d3 = 1.5d

= 1.5 × 52

= 78 mm

Thickness of single eye or rod end,

= 1.25 d

=1.25 × 52

=65 mm

Thickness of fork,

t1  = 0.75 d

= 0.75 × 52

= 39 say 40 mm

Thickness of pin head,

t2 = 0.5 d

= 0.5 × 52

= 26 mm

2. Failure of the knuckle pin in shear

Since the knuckle pin is in double shear, therefore load (P),

= 150 × 10³ / 4248

=35.3 N/mm2 = 35.3 MPa

Failure of the single eye or rod end in tension

The single eye or rod end may fail in tension due to the load. We know that load (P), 150 × 10³ = (d2 – d1) t × σt

= (104 – 52) 65 × σt

=3380 σt

σt   = 150 × 10³ / 3380

44.4 N / mm2 = 44.4 MPa

Failure of the single eye or rod end in shearing

The single eye or rod end may fail in shearing due to the load. We know that load (P), 150 × 103 = (d2 – d1) t × τ

=(104 – 52) 65 × τ

=3380 τ

= 150 × 10³ / 3380

=44.4 N/mm2 = 44.4 MPa

Failure of the single eye or rod end in crushing

The single eye or rod end may fail in crushing due to the load. We know that load (P), 150 × 103 = d1 × t × σc

=52 × 65 × σc

=3380 σc

σc   = 150 × 10³ / 3380

=44.4 N/mm² = 44.4 MPa

Failure of the forked end in tension

The forked end may fail in tension due to the load. We know that load (P), 150 × 10³ = (d2 – d1) 2 t1 × σt

= (104 – 52) 2 × 40 × σt

=4160 σt

σt   = 150 × 10³ / 4160

=36 N/mm² = 36 MPa

Failure of the forked end in shear

The forked end may fail in shearing due to the load. We know that load (P),

(P), 150 × 103 = d1 × t × σc

=52 × 65 × σc

=3380 σc

σc   = 150 × 10³ / 3380

=44.4 N/mm² = 44.4 MPa

Failure of the forked end in tension

The forked end may fail in tension due to the load. We know that load (P), 150 × 10³ = (d2 – d1) 2 t1 × σt

=(104 – 52) 2 × 40 × σt

=4160 σt

σt   = 150 × 10³ / 4160

=36 N/mm² = 36 MPa

Failure of the forked end in shear

The forked end may fail in shearing due to the load. We know that load (P),

15010³  = (d2 – d1) 2 t1 × σt x τ

=(104 – 52) 2 × 40 × τ

=4160 τ

= 150 × 10³ / 4160

=36 N/mm2 = 36 MPa

Failure of the forked end in crushing

The forked end may fail in crushing due to the load. We know that load (P), 150 × 103 = d1 × 2t1 × σc

=52 × 2 × 40 × σc

=4160 σc

σc  = 150 × 10³ / 4180

= 36 N/mm2 = 36 MPa

From above, we see that the induced stresses are less than the given design stresses, therefore the joint is safe.

(i) A 50 mm diameter solid shaft is welded to a flat plate by 10 mm fillet weld as shown in Fig. Find the maximum torque that the welded joint can sustain if the maximum

shear stress intensity in the weld material is not to exceed 80 MPa. 

Solution. 

Given :

d = 50 mm s = 10 mm

τmax = 80 MPa = 80 N/mm2

Let T = Maximum torque that the welded joint can sustain.

We know that the maximum shear stress (τmax),

= 2.83T

πsd2

2.83T

= 80 × 78550 / 2.83

= 2.22 × 106 N-mm = 2.22 kN-m

A plate 1 m long, 60 mm thick is welded to another plate at right angles to each other by 15 mm fillet weld, as shown in Fig. Find the maximum torque that the welded joint can sustain if the permissible shear stress intensity in the weld material is not to exceed 80 MPa. Solution.

Given:

= 1m = 1000 mm

; Thickness       = 60 mm ;

= 15 mm ;

= 80 MPa = 80 N/mm2

Let T = Maximum torque that the welded joint can sustain We know that the maximum shear stress (τmax),

= 4.242T / (s x l²)

= 4.242T / (15 x 1000²)

=0.283 T / 10⁶ T = 80 × 10⁶ / 0.283

283 × 106 N-mm = 283 kN-m

A plate 100 mm wide and 12.5 mm thick is to be welded to another plate by means of parallel fillet welds. The plates are subjected to a load of 50 kN. Find the length of the weld so that the maximum stress does not exceed 56 MPa. Consider the joint first under static loading and then under fatigue loading.

Solution.

Given:

Width = 100 mm Thickness = 12.5 mm

P = 50 kN = 50 × 10³ N ; τ = 56 MPa = 56 N/mm2

Length of weld for static loading

Let l = Length of weld, and

= Size of weld = Plate thickness = 12.5 mm

We know that the maximum load which the plates can carry for double parallel fillet welds (P),

=50 × 10³  =1.414 s × l × τ

=1.414 × 12.5 × l × 56 = 990 l l = 50 × 103 / 990

=50.5 mm

Adding 12.5 mm for starting and stopping of weld run, we have

= 50.5 + 12.5

= 63 mm

Length of weld for fatigue loading

From Table 10.6, we find that the stress concentration factor for parallel fillet welding is 2.7. Permissible shear stress,

τ = 56 / 2.7

= 20.74 N/mm²

We know that the maximum load which the plates can carry for double parallel fillet welds (P),

50   10³  = 1.414 s × l × τ

=1.414 × 12.5 × l × 20.74

=367 l

= 50 × 103 / 367

= 136.2 mm

Adding 12.5 for starting and stopping of weld run, we have

= 136.2 + 12.5

= 148.7 mm

A double riveted lap joint is made between 15 mm thick plates. The rivet diameter and pitch are 25 mm and 75 mm respectively. If the ultimate stresses are 400 MPa in tension, 320 MPa in shear and 640 MPa in crushing, find the minimum force per pitch which will rupture the joint. If the above joint is subjected to a load such that the factor of safety is 4, find out the actual stresses developed in the plates and the rivets.

Solution.

Given :

t = 15 mm d = 25 mm p = 75 mm

σtu = 400 MPa = 400 N/mm2

τu  = 320 MPa = 320 N/mm2

σcu = 640 MPa = 640 N/mm2

Minimum force per pitch which will rupture the joint

Since the ultimate stresses are given, therefore we shall find the ultimate values of the resistances of the joint. We know that ultimate tearing resistance of the plate per pitch,

Ptu        = (p – d)t × σtu

=(75 – 25)15 × 400

=300000 N

Ultimate shearing resistance of the rivets per pitch,

Psu  = n × (π/4) x d² x τu

=2 x (π/4) (25)² x 320

=314200 N

Ultimate crushing resistance of the rivets per pitch,

Pcu = n × d × t × σcu

=2 × 25 × 15 × 640

=480000 N

From above we see that the minimum force per pitch which will rupture the joint is

=300000 N or 300 kN.

Actual stresses produced in the plates and rivets

Since the factor of safety is 4, therefore

safe load per pitch length of the joint = 300000 / 4

= 75000 N

Let σta τa and σca be the actual tearing, shearing and crushing stresses produced with a safe load of 75000 N in tearing, shearing and crushing. We know that actual tearing resistance of the plates (Pta),

75000 = ( p – d ) t × σta

=(75 – 25)15 × σta

=750 σta

σta  = 75000 / 750

= 100 N/mm2 = 100 MPa.

Actual shearing resistance of the rivets (Psa), 75000 = n × (π/4) x d² x τa

n × (π/4) x 25² x τa

=982 τa

τa  = 75000 / 982

= 76.4 N/mm2 = 76.4 MPa

Actual crushing resistance of the rivets (Pca), 75000 = n × d × t × σca

=2 × 25 × 15 × σca

=750 σca

σca    = 75000 / 750

=100 N/mm2 = 100 MPa

A double riveted double cover butt joint in plates 20 mm thick is made with 25 mm diameter rivets at 100 mm pitch. The permissible stresses are : σt = 120 MPa; τ = 100 MPa; σc = 150 MPa Find the efficiency of joint, taking the strength of the rivet in double shear as twice than that of single shear.

Solution.

Given :

t = 20 mm d = 25 mm p = 100 mm

σt = 120 MPa = 120 N/mm2

= 100 MPa = 100 N/mm2

σc = 150 MPa = 150 N/mm2

First of all, let us find the tearing resistance of the plate, shearing resistance and crushing resistance of the rivet.

(i) Tearing resistance of the plate

We know that tearing resistance of the plate per pitch

length, Pt = (p – d ) t × σt

= (100 – 25) 20 × 120

=180000 N

(ii) Shearing resistance of the rivets

Since the joint is double riveted butt joint, therefore the strength of two rivets in double shear is taken. We know that shearing resistance of the rivets,

Ps     = n × 2 × (π / 4) x d² x τ

=2 x 2 x (π / 4 ) (25)2 100

=196375 N

Crushing resistance of the rivets

Since the joint is double riveted, therefore the strength of two rivets is taken. We know that crushing resistance of the rivets,

Pc     = n × d × t ×σc

=2 × 25 × 20 × 150

=150000 N

Strength of the joint       = (Least of Pt, Ps and Pc)

= 150 000 N

Efficiency of the joint

We know that the strength of the unriveted or solid plate,

= p × t × σt

=100 × 20 × 120

=240000 N

Efficiency of the joint = (Least of Pt , Ps and Pc) / P =150000 / 240000

= 0.625 or 62.5%