Solution of assignment problems (Hungarian Method)

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

(i) Examine the rows successively until a row with exactly one zero is found. Mark that zero by  , that means an assignment is made there . Cross ( ×) all other zeros in its column. Continue this until all the rows have been examined.

(ii) Examine the columns successively until a columns with exactly one zero is found. Mark that zero by  , that means an assignment is made there . Cross ( × ) all other zeros in its row. Continue this until all the columns have been examined  

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Solution:

Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

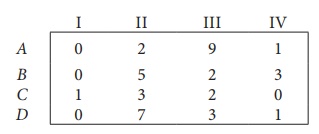
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

Examine the rows with exactly one zero. First three rows contain more than one zero. Go to row D. There is exactly one zero. Mark that zero by  (i.e) job D is assigned to machine I. Mark other zeros in its column by × .

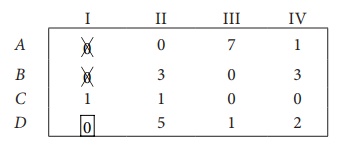
Step 4: Now examine the columns with exactly one zero. Already there is an assignment in column I. Go to the column II. There is exactly one zero. Mark that zero by . Mark other zeros in its rowby × .

Column III contains more than one zero. Therefore proceed to Column IV, there is exactly one zero. Mark that zero by . Mark other zeros in its row by × .

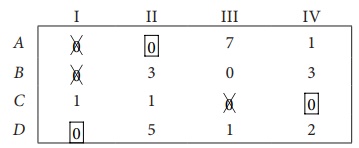
Step 5: Again examine the rows. Row B contains exactly one zero. Mark that zero by .

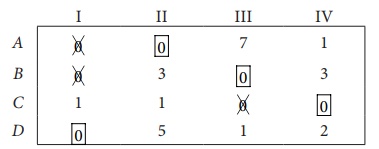
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

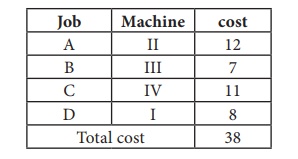
The optimal assignment (minimum) cost

= ₹ 38

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

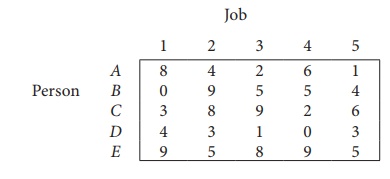
Solution:

Here the number of rows and columns are equal.

∴ The given assignment problem is balanced.

Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

The cost matrix of the given assignment problem is

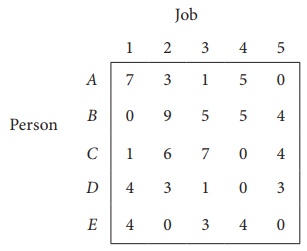
Column 3 contains no zero. Go to Step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

Examine the rows with exactly one zero. Row B contains exactly one zero. Mark that zero by  (i.e) PersonB is assigned to Job 1. Mark other zeros in its column by × .

Now, Row C contains exactly one zero. Mark that zero by . Mark other zeros in its column by × .

Now, Row D contains exactly one zero. Mark that zero by . Mark other zeros in its column by × .

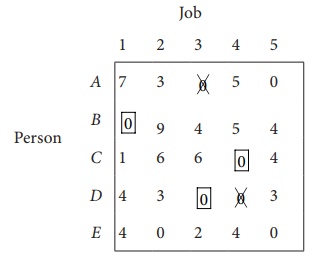
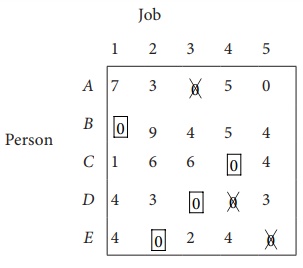
Row E contains more than one zero, now proceed column wise. In column 1, there is an assignment. Go to column 2. There is exactly one zero. Mark that zero by . Mark other zeros in its row by × .

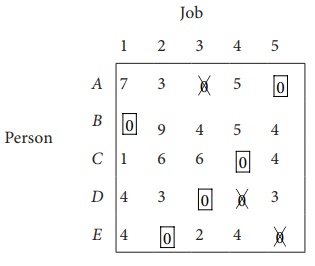
There is an assignment in Column 3 and column 4. Go to Column 5. There is exactly one zero. Mark that zero by . Mark other zeros in its row by × .

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

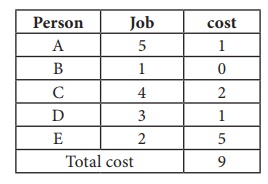
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

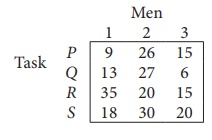
Solution:

Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

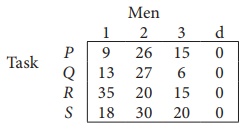
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

Step 2 :

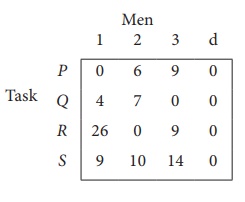
Step 3 (Assignment) :

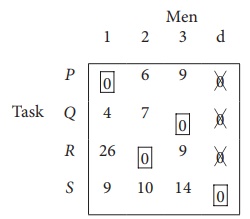
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

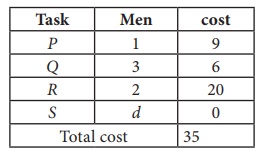
The optimal assignment (minimum) cost = ₹ 35