Methods of finding initial Basic Feasible Solutions: North-West Corner Rule (NWC)

Methods of finding initial Basic Feasible Solutions

There are several methods available to obtain an initial basic feasible solution of a transportation problem. We discuss here only the following three. For finding the initial basic feasible solution total supply must be equal to total demand.

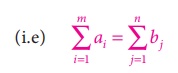
Method: North-West Corner Rule (NWC)

It is a simple method to obtain an initial basic feasible solution. Various steps involved in this method are summarized below.

Step 1: Choose the cell in the north- west corner of the transportation Table10.1 and allocate as much as possible in this cell so that either the capacity of first row (supply)is exhausted or the destination requirement of the first column(demand) is exhausted. (i.e) x11 = min(a1,b1)

Step 2: If the demand is exhausted (b1 < a1), move one cell right horizontally tothe second column and allocate as much as possible.(i.e) x12= min (a1 â€“x11, b2)

If the supply is exhausted (b1 > a1), move one cell down vertically to the second row and allocateas much as possible.(i.e)x21 = min (a2,b1 â€“ x11)

If both supply and demand are exhausted move one cell diagonally and allocate as much as possible.

Step 3: Continue the above procedure until all the allocations are made

Example 10.1

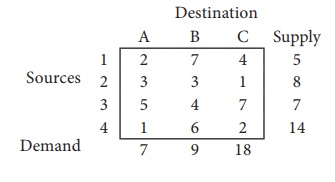
Obtain the initial solution for the following problem

Solution:

Here total supply = 5+8+7+14=34, Total demand = 7+9+18=34

(i.e) Total supply =Total demand∴The given problem is balanced transportation problem.

∴ we can findan initial basic feasible solution to the given problem.

From the above table we can choose the cell in the North West Corner. Here the cell is (1,A)

Allocate as much as possible in this cell so that either the capacity of first row is exhausted or the destination requirement of the first column is exhausted.

i.e. x11 = min (5,7) = 5

Reduced transportation table is

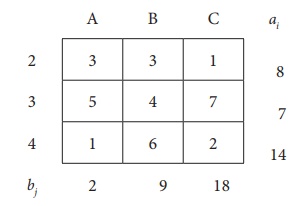
Now the cell in the North west corner is (2, A)

Allocate as much as possible in the first cell so that either the capacity of second row is exhausted or the destination requirement of the first column is exhausted.

i.e. x12 = min (2,8) = 2

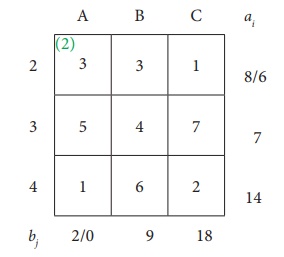
Reduced transportation table is

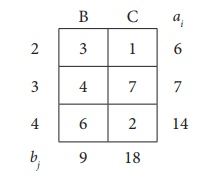
Here north west corner cell is (2,B) Allocate as much as possible in the first cell so that either the capacity of second row is exhausted or the destination requirement of the second column is exhausted.

i.e. x22 = min (6,9) = 6

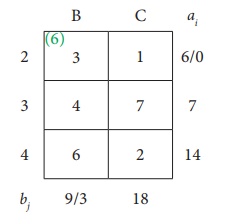
Reduced transportation table is

Here north west corner cell is (3,B).

Allocate as much as possible in the first cell so that either the capacity of third row is exhausted or the destination requirement of the second column is exhausted.

i.e. x32 = min (7,3) = 3

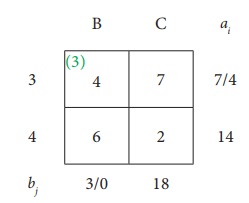
Reduced transportation table is

Here north west corner cell is (3,C) Allocate as much as possible in the first cell so that either the capacity of third row is exhausted or the destination requirement of the third column is exhausted.

i.e. x33 = min (4,18) = 4

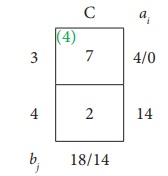
Reduced transportation table and final allocation is x44 = 14

Thus we have the following allocations

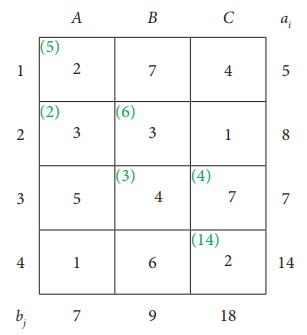
Transportation schedule : 1→ A, 2→A, 2→B, 3→B, 3→C, 4→C

The total transportation cost.

= (5 × 2) + (2 × 3) +(6 × 3)+(3 × 4)+(4 × 7) + (14 × 2)

= Rs.102

Example 10.2

Determine an initial basic feasible solution to the following transportation problem using North West corner rule.

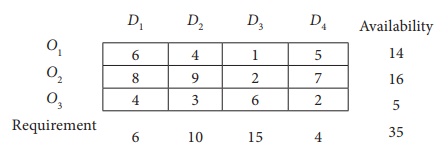
Here Oi and Dj represent ith origin and jth destination.

Solution:

Given transportation table is

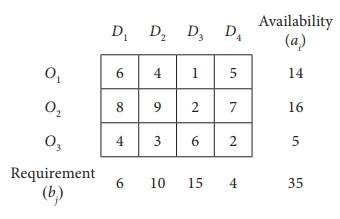
Total Availability = Total Requirement

∴ The given problem is balanced transportation problem.

Hence there exists a feasible solution to the given problem.

First allocation:

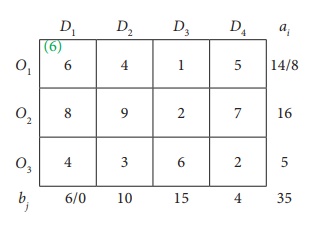
Second allocation:

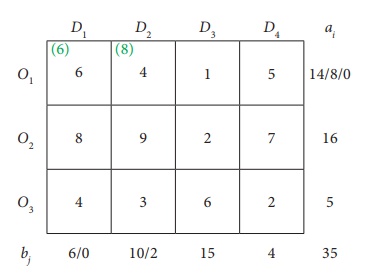
Third Allocation:

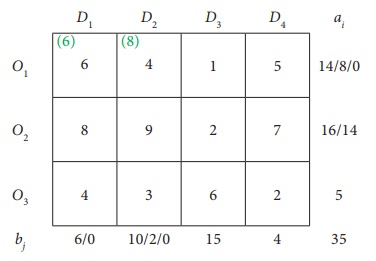
Fourth Allocation:

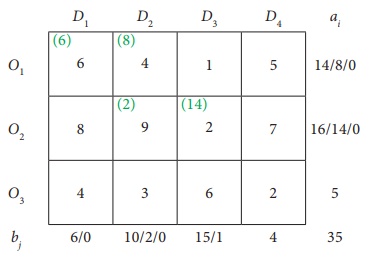
Fifth allocation:

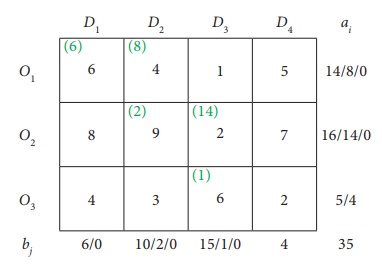
Final allocation:

Transportation schedule : O1→ D1, O1→D2, O2→D2, O2→D3, O3→D3, O3→D3.

The transportation cost

= (6 × 6)+(8 × 4)+(2 × 9)+(14 × 2)+(1 × 6)+(4 × 2) =Rs.128