Sample Problems and Important Short Answers: Linear Time Invariant Discrete Time Systems

1. States the properties of convolution

 i).Commutative property of convolution

x(n) ^∗h(n)=h(n) ^∗x(n)=y(n)

ii).Associative property of convolution

[x(n) ^∗h₁(n)]   ^∗ h₂(n)=x(n )^∗[ h₁(n). h₂(n)]

iii).Distributive property of convolution

x(n) ^∗[ h₁(n)+ h₂(n)] =x(n)   ^∗ h₁(n)+x(n) ^∗ h₂(n).

2.    Define non recursive and recursive of the following system.

When the output y(n) of the system depends upon present and past inputs then it is called non-recursive system. When the output y(n) of the system depends upon present and past inputs as well as past outputs, then it is called recursive system.

3.           Define convolution sum?

If x(n) and h(n) are discrete variable functions, then its convolution sum

y(n) is given by,

y(n)=_ x(k) h(n-k)

4. If x(n) and y(n) are discrete variable functions, what is its convolution sum.

The convolution sum is,

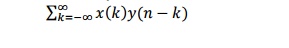
5.           Determine the system function of the discrete time system described by the difference equation.

Y(n) = 0.5y(n-1)+x(n)

Taking z-transform of both sides,

Y(z) = 0.5z^-1Y(z)+X(z)

H(z) = Y(z)/X(z) = 1/(1 – 0.5z ^-1)

6.           A causal LTI system has impulse response h(n), for which the z-transform is H(z) = (1+z^-1)/(1-0.5z^-1)(1+0.25z^-1). Is the system stable? Explain.

H(z) can be written in terms of positive powers of z as follows:

H(z) = z(z+1)/(z-0.5)(z+0.25)

Poles are at p₁ =0.5 and p₂ = -0.25. Since both the poles are inside unit circle. This system is stable.

7.    Check whether the system with system function H(Z) = (1/1-0.5z^-1)+(1/1-2z^-1) with ROC |z| < 0.5 is causal and stable?

H(z) = z/(z – 0.5) + z/(z - 2). Poles of this sys tem are located at z = 0.5 and z = 2. This system is not causal and stable, since all poles are not located inside unit circle.

8.    Is the discrete time system described by the difference equation y(n) = x(-n) is causal?

Here y(-2) = x(-(-2)) = x(2). This means output at n=-2 depends upon future inputs. Hence this system is not causal.

9. Consider a system whose impulse is h(t) = e^-|t|. Is this system is causal or non causal?

Here h(t) = e^-|t|

=e^-t  for t>=0

=e^t   for t<0

Since h(t) is not equal to zero for t<0, the system is non causal.

10. Find the step response of the system if the impulse response

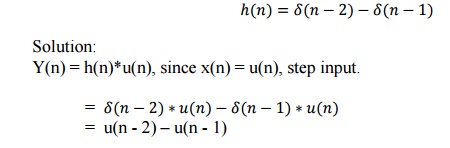
10.      Obtain the convolution of

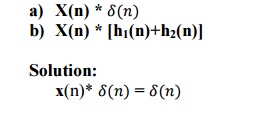
x(n)*[h₁(n)+h₂(2)] = x(n)*h₁(n) + x(n)*h₂(n)

12.      List the steps involved in finding convolution sum?

o folding

o Shifting

o Multiplication o Summation

13.      Consider an LTI system with impulse response h(n)= δ(n-*_“) for an input x(n),  find the Y(e^jω).

Here is the spectrum of output. By convolution theorem we can write,

14.      List the properties of convolution?

o Commutative property of convolution

x(n) * h(n) = h(n) * x(n) = y(n)

o Associative property of convolution

[ x(n) * h₁(n)] * h₂(n) = x(n) * [h₁(n) * h₂(n)]

o Distributive property of convolution

x(n) * [h₁(n) + h₂(n)] = x(n) * h₁(n) + x(n) * h₂(n)

15.      Define system function?

H(z)= Y(z) is called system function.It is the z transform of the unit sample X(Z) response h(n) of the system.

Sample Problems:

1. Consider the system described by the difference equation.

2. Given y[-1]=1 and y[-2]=0. Compute recursively a few terms of the following 2nd order DE:

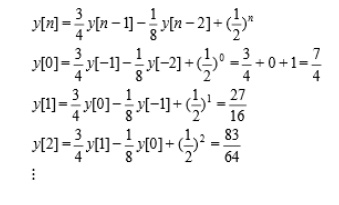
3. Compute the impulse response of the system described by,

4. Obtain the structures realization of LTI system

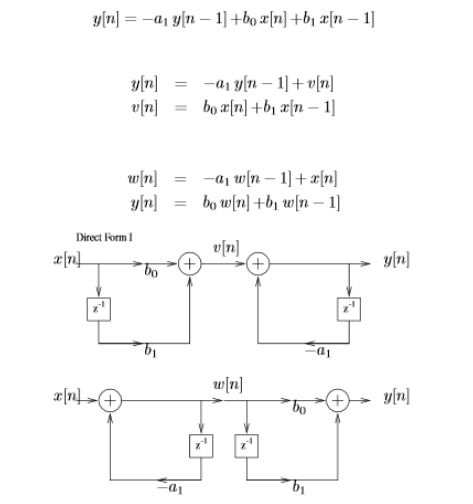
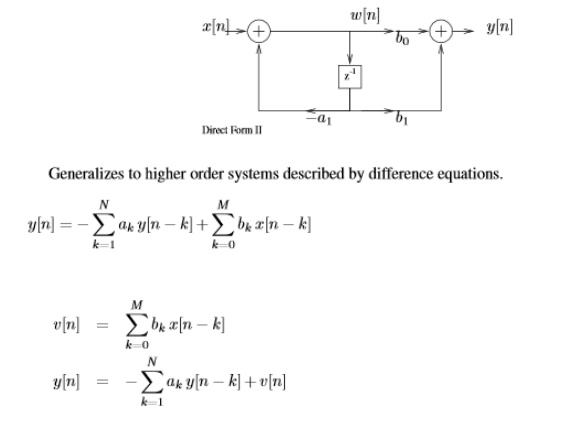
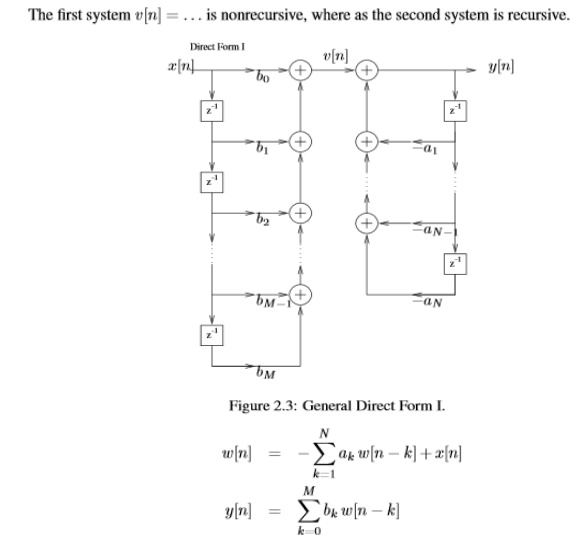
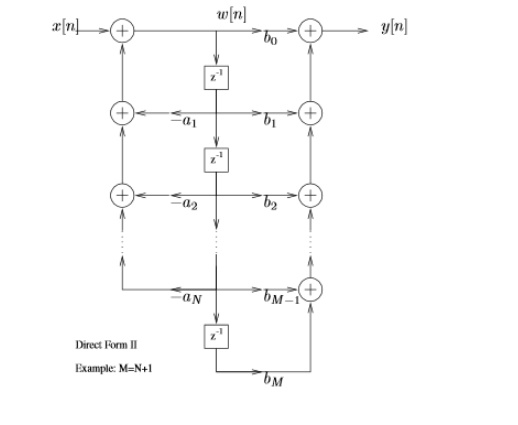
5. Find the convolution of x(n)=[1,1,1,1,2,2,2,2] with h(n)=[3,3,0,0,0,0,3,3] by using matrix method.

Solution: By using matrix method, N=8