Chapter: Control Systems : Stability and Compensator Design
Relative stability
Relative stability
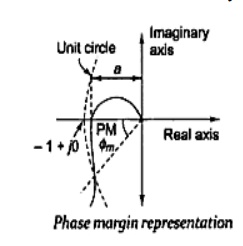
The main disadvantage of a Bode plot is that we have to draw and consider two different curves at a time, namely, magnitude plot and phase plot. Information contained in these two plots can be combined into one named polar plot. The polar plot is for a frequency range of 0<w<α . while the Nyquist plot is in the frequency range of - α<w<α. The information on the negative frequency is redundant because the magnitude and real part of G(jw) an are even functions. In this section. We consider how to evaluate the system performance in terms of relative stability using a Nyquist plot. The open-loop system represented by this plot will become unstable beyond a certain value. As shown in the Nyquist plot of Fig. the intercept of magnitude 'a on the negative real axis corresponds lost phase shift of - 180° and - 1 represents the amount of increase in gain that can be tolerated before closed-loop system tends toward instability. As 'a' approaches (-1+ j0) point the relative stability is reduced; the gain and phase margins are represented as follows in the Nyquist plot.
Gain margin
As system gain is increased by a factor 1/a, the open loop magnitude of G ( jw)H( jw) will increase by a factor a( 1/a) = 1 and the system would be driven to instability. Thus, the gain margin is the reciprocal of the gain at the frequency at which the phase angle of the Nyquist plot is - 1800. The gain rnargin, usually measured in dB, is a positive quantity given by
GM = -20log a dB

Phase Margin фm
Importance of the phase margin has already in the content of Bode. Phase margin is defined as the change in open-loop phase shift required al unity gain to make a closed loop system unstable. A closed-loop system will be unstable if the Nyquist plot encircles -1 +j0 point. Therefore, the angle required to make this system marginally stable in a closed loop is the phase margin .In order to measure this angle, we draw a circle with a radius of 1, and find the point of intersection of the Nyquist plot with this circle, and measure the phase shift needed for this point to be at an angle of 1800. If may be appreciated that the system having plot of Fig with larger PM is more stable than the one with plot of Fig.
Related Topics