Nyquist Stability Criteria

Nyquist Stability Criteria:

The Routh-Hurwitz criterion is a method for determining whether a linear system is stable or not by examining the locations of the roots of the characteristic equation of the system. In fact, the method determines only if there are roots that lie outside of the left half plane; it does not actually compute the roots. Consider the characteristic equation.

To determine whether this system is stable or not, check the following conditions

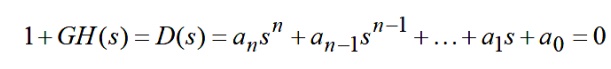
1. Two necessary but not sufficient conditions that all the roots have negative real parts are

a) All the polynomial coefficients must have the same sign.

b) All the polynomial coefficients must be nonzero.

2. If condition (1) is satisfied, then compute the Routh-Hurwitz array as follows

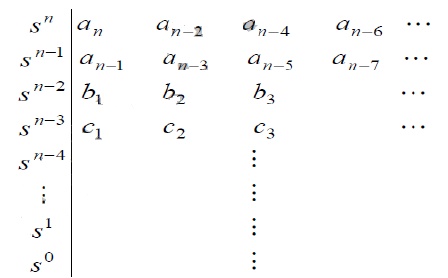
Where the ai‘S are the polynomial coefficients, and the coefficients in the rest of the table are computed using the following pattern

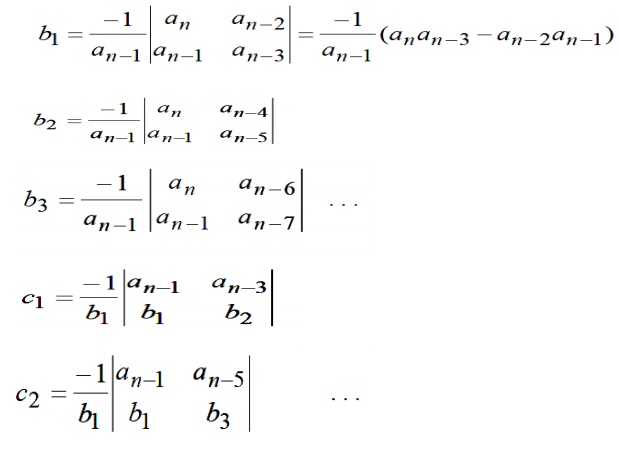
3. The necessary condition that all roots have negative real parts is that all the elements of the first column of the array have the same sign. The number of changes of sign equals the number of roots with positive real parts.

4. Special Case 1: The first element of a row is zero, but some other elements in that row are nonzero. In this case, simply replace the zero elements by " ", complete the table development, and then interpret the results assuming that " " is a small number of the same sign as the element above it. The results must be interpreted in the limit as ε to 0.

5. Special Case 2: All the elements of a particular row are zero. In this case, some of the roots of the polynomial are located symmetrically about the origin of the s-plane, e.g., a pair of purely imaginary roots. The zero rows will always occur in a row associated with an odd power of s.

The row just above the zero rows holds the coefficients of the auxiliary polynomial. The roots of the auxiliary polynomial are the symmetrically placed roots. Be careful to remember that the coefficients in the array skip powers of s from one coefficient to the next.

Let P = no. of poles of q(s)-plane lying on Right Half of s-plane and encircled by s-plane contour.

Let Z = no. of zeros of q(s)-plane lying on Right Half of s-plane and encircled by s-plane contour.

For the CL system to be stable, the no. of zeros of q(s) which are the CL poles that lie in the right half of s-plane should be zero. That is Z = 0, which gives N = -P.

Therefore, for a stable system the no. of ACW encirclements of the origin in the q(s)-plane by the contour Cq must be equal to P.

Nyquist modified stability criteria

 We know that q(s) = 1+G(s)H(s) Therefore G(s)H(s) = [1+G(s)H(s)] – 1

The contour Cq, which has obtained due to mapping of Nyquist contour from s-plane to q(s)-plane (ie)[1+G(s)H(s)] -plane, will encircle about the origin.

The contour CGH, which has obtained due to mapping of Nyquist contour from s-plane to G(s)H(s) -plane, will encircle about the point (-1+j0).

Therefore encircling the origin in the q(s)-plane is equivalent to encircling the point -1+j0 in the G(s)H(s)-plane.

Problem

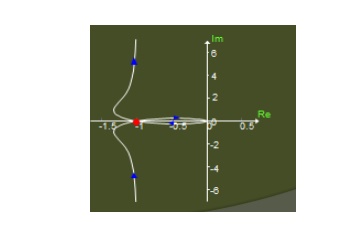
Sketch the Nyquist stability plot for a feedback system with the following open-loop transfer function

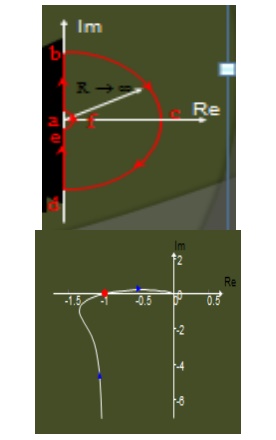
Section de maps as the complex image of the polar plot as before