Chapter: Discrete Time Systems and Signal Processing : Discrete Time System Analysis
Relationship Between Fourier Transform and Z Transform
RELATIONSHIP BETWEEN FOURIER
TRANSFORM AND Z TRANSFORM
There is
a close relationship between Z transform and Fourier transform. If we replace
the complex variable z by e –jω, then z transform is reduced to Fourier transform.
Z
transform of sequence x(n) is given by

Fourier transform of sequence x(n) is given by
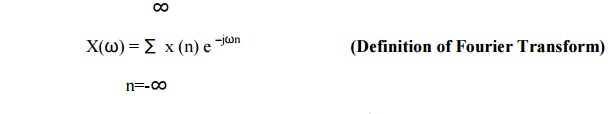
Complex
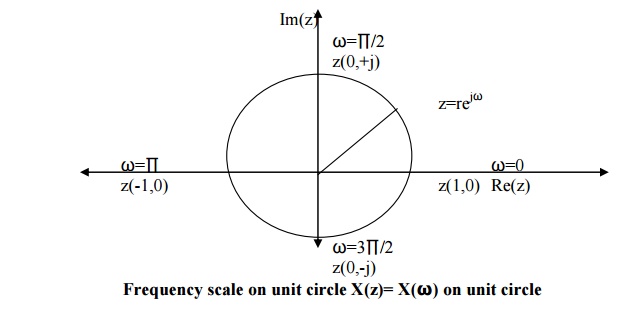
variable z is expressed in polar form as Z= rejω where r= |z| and ω is ∟z. Thus we can be written as
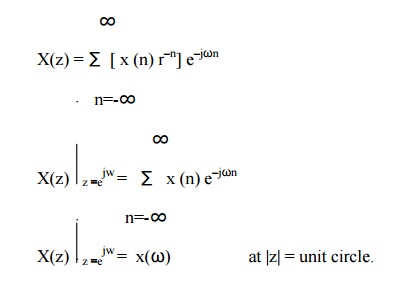
Thus,
X(z) can be interpreted as Fourier Transform of signal sequence (x(n) r–n).
Here r–n grows with n if r<1 and decays with n if r>1. X(z)
converges for |r|= 1. hence Fourier transform may be viewed as Z transform of
the sequence evaluated on unit circle. Thus The relationship between DFT and Z
transform is given by
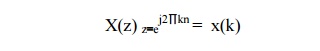
The
frequency ω=0 is
along the positive Re(z) axis and the frequency ∏/2 is along the positive Im(z) axis. Frequency ∏ is along the negative Re(z) axis
and 3∏/2 is along the negative Im(z)
axis.
Related Topics